Games202笔记：环境光照（Environment Lighting）

目录

回顾

环境光照（Environment Lighting），用一张图记录，在场景中任意方向都能看到的光照.

隐含概念：光照都是无限远的.

存储方式：球面贴图（Spherical Map），立方体贴图（Cube Map）.

来自环境光照的着色

给定环境光照，如果不考虑遮挡、阴影，如何计算shading（着色）？

答：这种操作，工业界有个非正式名称IBL（Image-Based Lighting，基于图像的照明）.

给定光照下，任何物体上任何一个shading point，如何得到其颜色值？

自然想到解渲染方程（rendering equation）.

\[L_0(p,\omega_o)=\int_{Ω^+}L_i(p,\omega_i)f_r(p,\omega_i,\omega_o)cos \theta_id\omega_i \]

由于光照来自各个方向，因此不再考虑可见性\(V(p,\omega_i)\).

蒙特卡洛积分法

通用解法：蒙特卡洛积分（Monte Carlo integration）

特点：

1）任何有限区间积分，都能用蒙特卡洛积分，用采样数据做数值上的近似.

2）需要大量的样本，才能让结果接近期望值.

所以，该方法会非常慢，并非首选方法.

经典近似法

  • 如果BRDF是glossy，对应glossy材质，说明BRDF的积分域很小（small support）；

  • 如果BRDF是diffuse，对应diffuse材质，说明BRDF平滑，也就是说其值变化不大.

img

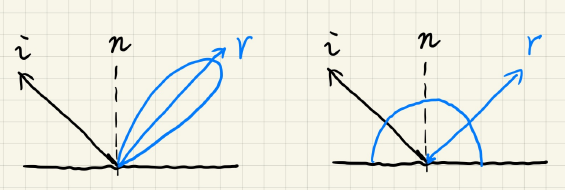
如果满足上面2个条件之一，对应：
1）积分域\(Ω\)很小；
2）g(x)变化很小，
就能将被积函数拆开. 参见Games202笔记：实时阴影（RTR Shadow） 实时渲染中的数学

\[\int_Ωf(x)g(x)dx≈\frac{\int_{Ω_G}f(x)dx}{\int_{Ω_G}dx}\cdot \int_Ω g(x)dx \]

其中，\(Ω_G\)代表g函数有值的范围.

因此，可将环境光照的渲染方程拆分：

\[L_o(p,\omega_o)≈\frac{\int_{Ω_{f_r}}L_i(p,\omega_i)d\omega_i}{\int_{Ω_{f_r}}d\omega_i}\cdot \int_{Ω^+}f_r(p,\omega_i,\omega_o)cos \theta_i d\omega_i \]

注意区分实时阴影的渲染方程：

\[L_o(p,\omega_o)≈\frac{\int_{Ω^+}V(p,\omega_i)d\omega_i}{\int_{Ω^+}d\omega_i}\int_{Ω^+}L_i(p,\omega_i)f_r(p,\omega_i,\omega_o)cos \theta_i d\omega_i \]

于是，可以分2部分对\(L_o(p,\omega_o)\)求解，每个部分都能用Split Sum求和.

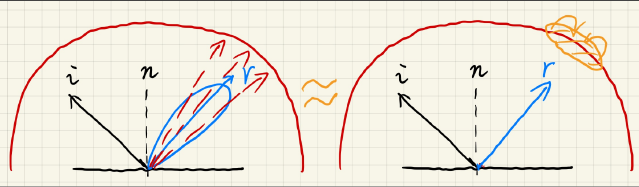
Split Sum第一项

预滤波环境光求\(L_i(p,\omega_i)\).

对环境光做预滤波（prefiltering）. 所谓滤波，就是模糊，是将像素周围几个点加起来做平均写回原位置.

img

根据原有的环境光照贴图，预生成一组包含多个层级（不同大小）的环境光照贴图，为Split Sum的光照项（Lighting Term）提供数据支持.

如果filter size位于2个层级之间，可以做三线性插值（trilinear interp）.

为什么要做prefiltering？

1）如果不做prefiltering，那么需要对glossy反射区域中对反射光线做采样，才能得到最终shading point值；

2）先做prefiltering，对反射区域的反射光线已经做了模糊处理，于是可以直接取镜面反射

注意：prefiltering需要在反射方向r对应的球面区域进行.

img

Split Sum第二项

预计算求\(\int_{Ω^+}f_r(p,\omega_i,\omega_o)cos \theta_i d\omega_i\).

如何求出后面一半这部分，而避免求积分（采样）？

答：预计算所有变量组合的值，针对粗糙度、颜色（菲涅尔项）等参数. 但是，如果直接构建涵盖所有参数组合的查找表，将导致超高维度的数据存储.

为求这部分积分的值，先回顾微表面（Microsurface）BRDF.

微表面BRDF，可参见计算机图形：材质和外观 微表面材质

img

\[f(i,o)=\frac{F(i,h)G(i,o,h)D(h)}{4(n,i)(n,o)} \]

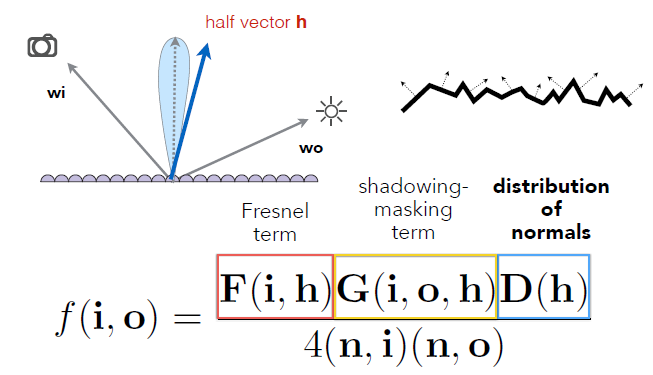
  • \(F(i,o)\) 菲涅尔项，如果入射光线几乎平行入射，那么大量光线被反射.
  • \(D(h)\) 法线分布，给定方向上，分布的值是多少
  • \(G(i,o,h)\) 几何项，修正微表面之间相互遮挡而产生阴影或无法观察到的情况.

对于几何遮蔽函数\(G(i,o,h)\)，用于描述微表面间的遮蔽（Shadowing）和遮挡（Masking）效应，确保能量守恒并增强物理真实性.

G项修正以下两种现象：

遮蔽（Shadowing）：入射光线被微表面凸起部分阻挡.
遮挡（Masking）：出射光线被微表面凸起部分遮挡.

注意：若不考虑G项，粗糙表面会在高光区域出现过亮的现象（违反能量守恒）.

G项与粗糙度关系：

低粗糙度（平滑表面）：G项接近1（遮蔽/遮挡效应弱）。

高粗糙度（粗糙表面）：G项显著降低（遮蔽/遮挡效应强）。

常用Smith GGX模型确定G项：将G项拆分为入射（\(G_1(\omega_i)\)）和出射（\(G_1(\omega_o)\)）两部分，

\[G(\omega_i,\omega_o)=G_1(\omega_i) * G_1(\omega_o)\\ G_1(\omega)=\frac{2(n\cdot \omega)}{(n\cdot \omega + \sqrt{α^2+(1-α^2)(n\cdot \omega)^2})} \]

其中，

  • \(\omega\) 光线方向，（\(\omega_i\)入射方向，\(\omega_o\)出射方向）
  • \(n\) 宏观表面法向量
  • \(α=roughness^2\) 粗糙度的平方（映射到0~1）

由此可知，模型确定后，G项是一个取决于\(n,\omega,α\)的常数. 其他G项模型，还有Beckmann模型、Schlick-GGX模型等.

接下来计算\(F(i,o)\)和\(D(h)\)两项.

1）计算菲涅尔项\(F(i,o)\)（常用Schlick近似）

\[\begin{aligned} F(i,o)=R(θ)&=R_0+(1-R_0)(1-cos θ)^5\\ R_0&=(\frac{n_1-n_2}{n_1+n_2})^2\\ \end{aligned} \]

其中，\(R_0\) 垂直入射时的基础反射率（如金属的Albedo，非金属的0.04）；\(θ\) 入射光与表面法线的夹角，即\(\omega_i,\omega_o\)夹角的一半.

2）计算 法线分布\(D(h)\)

如果要定义法线分布函数（Normal Distribution Function, NDF），需要将角度描述成一个分布，例如，Beckmann 分布

img

\[D(h)=\frac{e^{-\frac{tan^2θ_h}{α^2}}}{πα^2cos^4 θ_h} \]

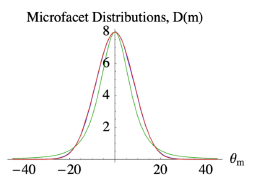
其中，

  • h：微表面法线（半角向量）
  • \(θ_h\) ：h与宏观表面法线的夹角
  • α：表面粗糙度参数（\(α=roughness^2\)）

物理含义：α 越大，微表面法线分布越分散（表面越粗糙）；\(\int_Ω D(h) cos θ_h dh = 1\)，反射光总量能量守恒；通过指数\(e^{-\frac{tan^2θ_h}{α^2}}\)模拟高光随角度快速衰减的特性.

如果我们用Schlick近似引入第二项，将\(R_0\)提取出来，那么

\[\begin{aligned} &\int_{Ω^+}f_r(p,\omega_i,\omega_o)cos θ_id\omega_i \\ =& \int_{Ω^+}\frac{F(i,h)G(i,o,h)D(h)}{4(n,i)(n,o)}cos θ_id\omega_i\\ =&\int_{Ω^+}\frac{F(i,h)f_r}{F}cos θ_id\omega_i, (f_r=G(i,o,h)D(h), F=4(n,i)(n,o))\\ ≈&\int_{Ω^+}[R_0+(1-R_0)(1-cos θ_i)^5]\frac{f_r}{F}cos θ_id\omega_i\\ =&R_0\int_{Ω^+}\frac{f_r}{F}(1-(1-cos θ_i)^5)cos θ_id\omega_i+\int_{Ω^+}\frac{f_r}{F}(1-cos θ_i)^5cos θ_id\omega_i \end{aligned} \]

其中，基础反射率\(R_0\)取决于材质，材质确定时\(R_0\)是常数.

现在每个积分对每个（粗糙度，入射角）组合生成一个值. 因此，每个积分会得到一个二维数组（纹理）. 当我们需要某个积分时，直接从该二维数组对应纹理中，根据入射角、粗糙度查找即可.

img

通过前面提到的Split Sum 2步的处理，能得到如下结果：

img

Split Sum近似

在工业界，将积分转化为求和：

\[L_o(p,\omega_o)=\frac{1}{N}\sum_{k=1}^N\frac{L_i(l_k)f(l_k,v)cos θ_{l_k}}{p(l_k,v)}≈(\frac{1}{N}\sum_{k=1}^NL_i(l_k))(\frac{1}{N}\sum_{k=1}^N\frac{f(l_k,v)cos θ_{l_k}}{p(l_k,v)}) \]

这就是所谓分离求和(split sum)，一种基于IBL的数学优化方法，通过将复杂的镜面反射积分拆分为2个独立部分进行预计算，显著降低运行时计算开销.

来自环境光照的阴影

通常来说，很难做到在实时渲染中实现阴影.

不同角度看环境光照：

  • 当做多个光源（many-light）问题

因为每个光源，都要生成其shadow map，那么代价线性于光源数量.

  • 当做采样（sampling）问题

对空间中各个不同方向光照进行采样，需要大量采样样本，采样的难度不在于往各个方向去看，而是往不同方向看visibility是什么.

  • 工业解决方案

为主光源（最亮的光源）生成阴影（或者稍微多点，2、3个阴影）

相关研究：

1）Imperfect shadow maps，做的Indirection illumination部分的阴影；
2）Light cuts，解决off-light（离线渲染）中的many-light问题：把场景中反射物当做很多小的光源，很多反射物意味着很多光源，将这些光源归类，然后整体照亮某一个点，照亮出来的结果是什么；
3）RTRT（real time ray tracing），一种通过硬件加速（如NVIDIA RTX显卡）实现高质量实时渲染的技术；
4）PRT(Precomputed Radiance Transfer），能得到非常精确的来自环境光的阴影.

背景知识

频率、滤波

傅里叶级数展开：任何一个函数，都能写成 “常数 + 一系列sin + cos”的形式.

img

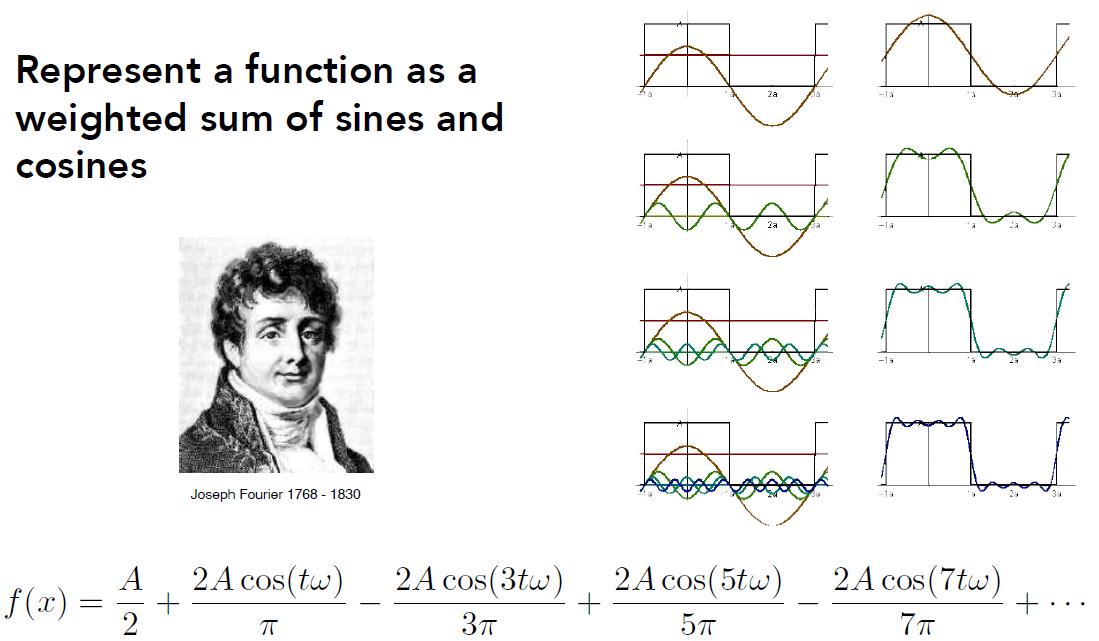
上图中，sin项的系数为0.

傅里叶变换：将一个函数从时域变换到频域

下图中，我们逐渐增加频率的项

img

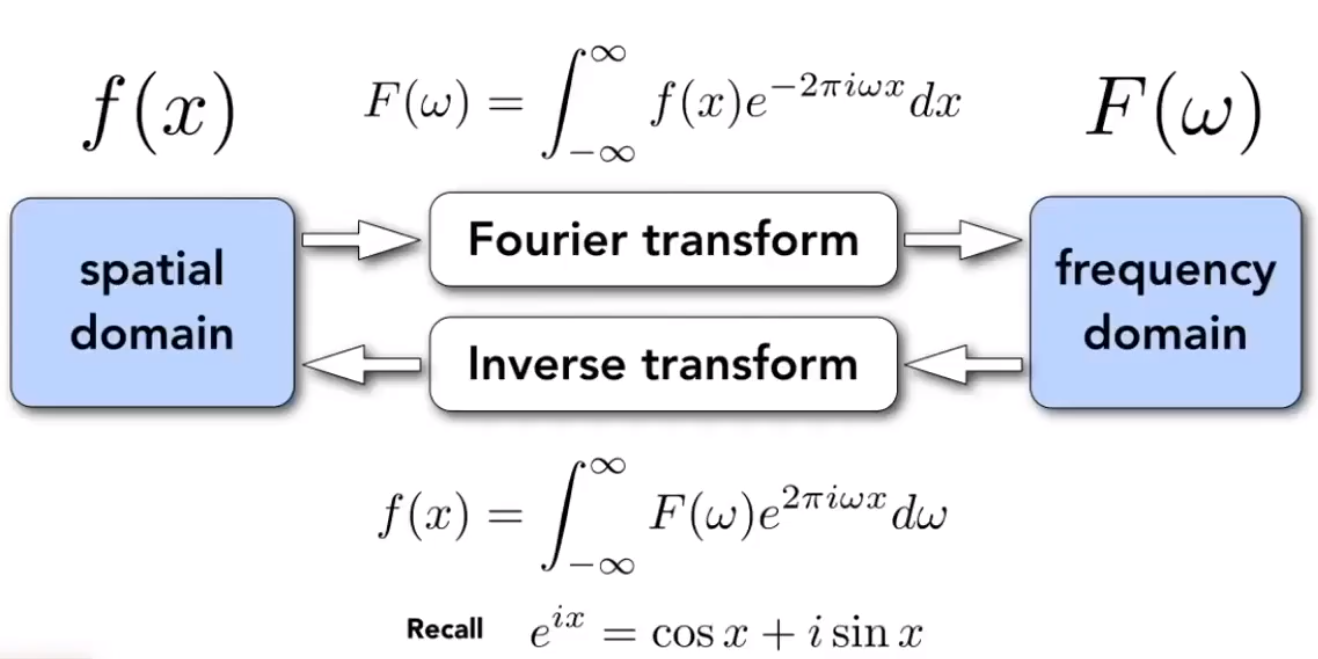
滤波，就是要去掉一系列频率上的内容.

如下图，左图是二维图形（时域），右图是其对应频域，俗称频谱.

中间亮点是高频的内容，代表变化剧烈；
四周暗的部分，代表变化小.

img

滤波：现在，我们对图像进行低通滤波，只留下低频的部分，然后将低频部分还原成图像，会得到相对模糊的图像.

img

卷积定理（Convolution Theorem）

时域上做卷积 = 频域上做乘积

img

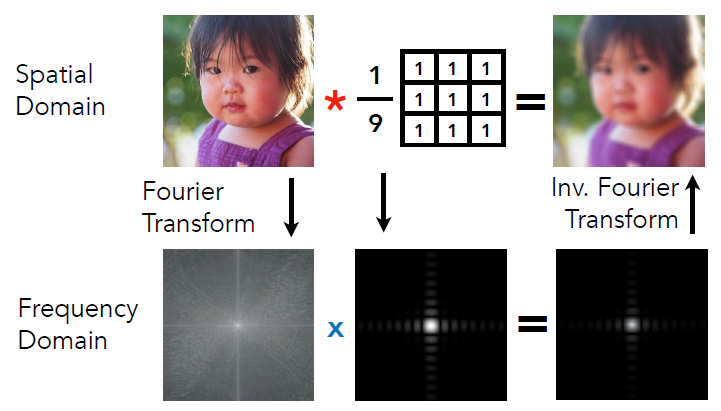
两个函数相乘，然后做积分，就可以理解成时域上的卷积 = 频域上2个信号相乘

只有有一个函数是低频的，那么它们的积分也是低频的，即积分的频率取决于\(f(x),g(x)\)中最低的频率.

低频 = 光滑函数/改变缓慢等

基函数（Basic Function）

将一个函数转化成其他函数的线性组合. 如下式中，原函数\(f(x)\)可以转化成一系列函数\(B_i(x)\)乘以一个系数\(c_i\)的和，则称\(B_i\)为基函数（Basic function）.

\[f(x)=\sum_{i}c_i\cdot B_i(x) \]

傅里叶级数展开，就是一系列的基函数.

常用基函数：

  • Spherical Harmonics(SH)（球谐函数）
  • Wavelet（小波）
  • Zonal Harmonics（区域谐函数）
  • Spherical Gaussian（SG，球面高斯函数）
  • Piecewise Constant（分段常数）

注解：

1）高斯函数指指数函数

\[G(x)=Ae^{-\frac{(x-μ)^2}{2σ^2}} \]

其中，A表示幅值，μ表示期望，σ表示标准差.

2）球面高斯函数

\[G(\bm{v})=e^{λ(μ\cdot \bm{v}-1)} \]

其中，\(\bm{v}\)单位方向向量，μ主方向，λ带宽参数

如何从实时环境光、全局光照中，计算阴影呢？

有3种办法：

  • Spherical Harmonics
  • Prefiltered env. lighting
  • Precomputed Radiance Transfer (PRT)

球谐函数

球谐函数（Spherical Harmonics, SH）是定义在单位球面上的一组2D正交基函数\(B_i(\omega)\)，用于描述球面上的任意分布.

特点：

1）任意2个不同基函数之间的内积（inner product）为0.

函数内积有点类似于向量点积的概念，向量点积是各个分量相乘再求和，函数内积是2个函数相乘再积分.

2）SH旋转不变.

3）SH基函数计算成本不高.

函数的内积定义：

\[\lang f_i(x),f_j(x) \rang = \int f_i(x)f_j(x)dx \]

注意：方程是在定义域内积分，即x轴上.

球面函数的内积：

\[\lang f_i(\bm{n}),f_j(\bm{n}))=\int_{\bm{n}\in Θ}f_i(\bm{n})f_j(\bm{n})d\bm{n} \]

其中，\(\bm{n}\in Θ\)代表在单位球面方向上进行积分.

标准正交函数集（orthonormal set）也是一个正交集，附加条件是该集合中的任意一个函数与自身的内积都为1. 一组函数\(\{f_j()\}\)是标准正交的条件：

\[\lang f_i(),f_j()\rang = \begin{cases} 0, where\space i\neq j,\\ 1, where\space i=j \end{cases} \]

标准正交基优点：想要找到最接近目标函数的近似值很简单. 每个基函数的权重系数都是目标函数\(f_{target}()\)与相应基函数的内积：

\[k_j=\lang f_{target}(), f_j() \rang,\\ f_{target}()≈\sum_{j=1}^nk_jf_j(). \]

实践中，该积分只能通过数值方法进行计算，通常采样蒙特卡洛采样，对平均分布在球面上的n个方向进行计算，然后再求平均值.

SH基函数可以按照频带（frequency band）进行排列. 第一个基函数是一个常数；接下来三个基函数是线性变化，它们在球面上缓慢变化；再接下来五个基函数是变化稍快的二次函数... 频率较低的函数，即在球面上变化缓慢，如Irradiance等，可用相对较少的SH系数来精确表示.

类似于一维情况下的傅里叶函数，每一层级基函数频率不同，个数不同. 下图是Spherical Harmonics的可视化，

  • l=0：第0层（layer），它是一个uniform，值都一样；
  • l=1：第1层，有3个函数，某个半球上有一个值，对称的半球上有不同的值，各种函数朝向不一样；
  • l=2：第2层，有5个函数；
  • l=3：第3层，有2*3+1=7个函数；
    ...

img

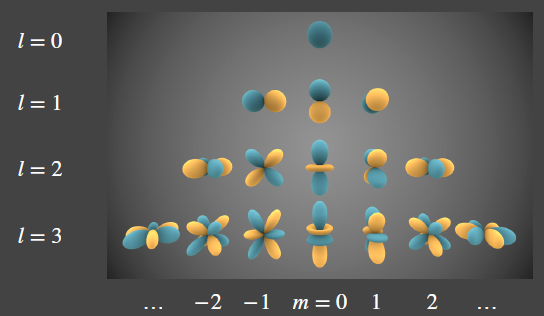
有人给不同行的（基）函数起不同名字，l=0的函数，叫“第0阶SH”；l=1的函数，叫“第1阶SH”；l=2的函数，叫“第2阶SH”；... 每一阶（层）有2l+1个函数，编号从“-l...-2,-1,0,1,2,...,l”.

当投影到SH的时候，所获得的系数代表了投影函数在各个频率上的振幅（amplitude），即频谱（frequency spectrum），代表了信号或波形中各个频率成分中的强度分布. 在该光谱域（spectral domain），有一个基本性质：2个函数乘积的积分等于函数投影系数的点积. 该特性能使我们能高效地计算光照积分.

既然可以做2D傅里叶变换，为什么不在球面按θ、φ展开2D平面，然后做2D傅里叶变换，最后还原到球面？

如果展开球面，再做2D傅里叶变换，做些近似，最后还原到球面，可能会产生一些缝隙. 而SH本身定义在球面上，因此在球面上做处理并不会产生缝隙问题. 通常只需要4阶即可.

1）如何确定每个SH基函数\(B_i(\omega)\)？

可以用Legendre多项式.

2）如果要将任一函数展开成Spherical Harmonics，那么前面的系数\(c_i\)是什么？

任何一个SH Basic function，求基函数的系数\(c_i\)的过程，称为投影.

\[c_i=\int_{Ω}f(\omega)B_i(\omega)d\omega \]

对不同方向进行采样，从而计算出该积分.

求出了系数，又知道基函数，就能通过SH的性质（多项式求和）还原初始函数. 通常，取前面4阶即可.

关于投影，可类比向量在三维坐标系中的表示. 比如，有向量V，它在坐标系中的表示是\(V_x,V_y,V_z\)，这三个值就是在坐标轴上的投影，所以，

\[\bm{V}=V_x*\bm{x}+V_y*\bm{y}+V_z*\bm{z} \]

其中，\(\bm{x},\bm{y},\bm{z}\)是基函数，\(V_x,V_y,V_z\)是系数，\(\bm{V}\)刚好是基函数的展开.

PRT

前面讲过，环境光沿着镜面反射方向，去查它的值，就像是看到镜子(specular)；

如果先把环境光先做prefiltering，沿着镜面反射方向，在模糊的Environment Light（环境光）上查它的值，看起来像是diffuse.

img

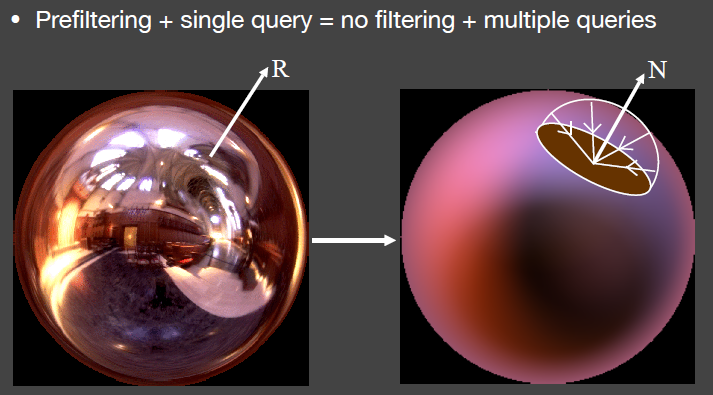
diffuse BRDF 看起来像低通滤波一样：

\[E_{IM}=A_IL_{IM} \]

下图，意味着只有前面3阶才有值，后面的值没有高频信息.

img

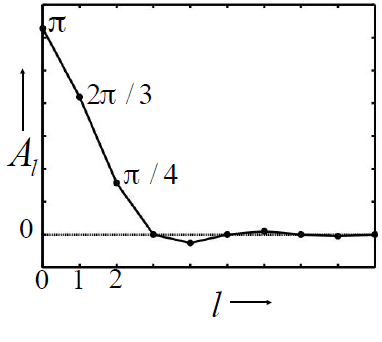
对于任何光照，只要材质是diffuse的，只需要前3阶的SH 描述光照，用其照亮diffuse物体. 与用更多阶的SH效果差别不大.

Sloan与02年提出PRT(Precomputed Radiance Transfer, 预计算Radiance传输). 基本思想：

\[L(o)=\int_Ω[L(i)][V(i)ρ(i,o)max(0,n\cdot i)]di \]

将Rendering equation 看做2部分：

1）与光照有关的Lighting: \(L(i)\)；

2）与光照无关的Light transport：\(V(i)ρ(i,o)max(0,n\cdot i)\)

将Lighting用基函数近似表示：

\[L(i)≈\sum l_iB_i(i) \]

其中，\(l_i\)是光照系数（lighting coefficent），\(B_i(i)\)是基函数（basis function）.

场景不变的情况下，对于任一shading point，物体的遮挡管线不变，即\(V(i)\)不变；物体表面材质不变，那么BRDF不变，即\(ρ(i,o)\)不变.

在其他所有东西都不变情况下，只有Lighting改变，它的Light transport就是一个球面函数.

对于diffuse物体

BRDF是一个常数，记为\(ρ\)

\[\begin{aligned} L(o) &= ρ\int_ΩL(i)V(i)max(0,n\cdot i)di\\ L(i) &≈ \sum l_iB_i(i)\\ \implies L(o) &≈ ρ\sum l_i\int_ΩB_i(i)V(i)max(0, n\cdot i)di \end{aligned} \]

注意：在PRT场合，可以直接交换积分与求和.

式子中\(\int_ΩB_i(i)V(i)max(0, n\cdot i)di\)这部分，刚好是球面函数投影到某个basic function的系数\(c_i\)，将其记为\(T_i\).
于是，

\[L(o)≈ρ\sum l_iT_i \]

这样，\(L(o)\)就能看做2个向量乘积.

代价：
场景中所有物体都不能动，如果运动，那么visibilty在很多地方发生变换；

注意：
1）V项与光源旋转无关，因为V项代表从shading point朝四面八方看，光源旋转不影响物体之间相互遮挡关系.
2）一个基函数，投影到其他任一基函数，就会得到0. 因为任意2个基函数是正交的（垂直）.

SH的基函数是正交的，有

\[\begin{aligned} \int_{Ω}B_i(i)\cdot B_j(i)di &= 1(i==j)\\ \int_{Ω}B_i(i)\cdot B_j(i)di &= 0(i\neq j) \end{aligned} \]

投影到SH空间:

\[l_i=\int_ΩL(i)\cdot B_i(i)di \]

重建（Reconstruction）：

\[L(i)≈\sum l_iB_i(i) \]

预计算light transport：

\[T_i≈\int_ΩB_i(i)V(i)max(0,n\cdot i)di \]

最终，实时渲染：

\[L(o)≈ρ\sum l_iT_i \]

于是，预计算lighting和light tranport的渲染方程可写成：

\[\begin{aligned} L_o(p,ω_o) &= \int_{Ω^+}[L_i(p,ω_i)][f_r(p,ω_i,ω_o)cos θ_iV(p,ω_i)]dω_i\\ L(ω_i) &≈ \sum_p c_pB_p(ω_i), T(ω_i)≈\sum_qc_qB_q(ω_i)\\ \implies L_o(p,ω_o) &= \int_{Ω^+}[L_i(p,ω_i)][f_r(p,ω_i,ω_o)cos θ_iV(p,ω_i)]dω_i\\ &= \sum_p\sum_q c_pc_q\int_{Ω^+}B_p(ω_i)B_q(ω_o)dω_i \end{aligned} \]

看起来复杂度是\(O(n^2)\)，但因为基函数是正交的，因此只有p=q时，才有值. 因此，复杂度仍然是\(O(n)\).

下图是diffuse渲染结果：
img
注：Inter = Inter-reflection，相互反射

图中，

  • No shadows是只考虑环境光照、不考虑阴影的渲染结果，整体无阴影；
  • Shadows是考虑环境光照、阴影的渲染结果，整体偏暗；
  • Shadows+Inter 考虑环境光照、反复反射的渲染结果，只有部分地方有阴影.

PRT：对于每个shading point，预计算lighting和light transport

shading point是每个几何形体的顶点（vertex）. 实际运算时，可以先计算三角形顶点的shading result，然后在三角形内部插值.

\[L_o(p,ω_o)=\int_{Ω^+}[L_i(p,ω_i)][f_r(p,ω_i,ω_o)cos θ_iV(p,ω_i)]dω_i \]

  • Shading result: \(L_o(p,ω_o)\)
  • Lighting: \(L_i(p,ω_i)\)
  • Light transport: \(f_r(p,ω_i,ω_o)cos θ_iV(p,ω_i)\)

Spherical Harmonics(SH，球谐函数) 是一系列基函数.

基函数性质：

1）分为不同的阶（或层），每一行对应一阶，每一行表示一个固定的频率. 随着l（layer）增加，能表示的频率越高.
2）每一种频率（每一层），有2l+1种不同类型的基函数.
3）任何一个二维函数都能投影到SH上面去，可以用一系列加权和描述任意一个二维函数.

\[f(x)=\sum_i c_i\cdot B_i(x) \]

同时，任意二维函数能从SH中恢复.

对于glossy物体

对于diffuse物体，不论视角如何旋转，看到的东西，看shading point，整个diffuse shading 即\(L(o)\)与视角无关；
对于glossy物体，与视角有关，有一个不同观察方向，就有不同的\(L(o)\).

\[\begin{aligned} L(o)&=\int_ΩL(i)V(i)ρ(i,o)max(0,n\cdot i)di\\ L(o)&≈\sum l_iT_i(o) \end{aligned} \]

代价：
1）任何一个顶点/shading point，都需要存一个transport matrix；
2）render时，需要做向量和矩阵的乘法，操作会比向量与向量做点乘复杂得多.

小波（Wavlet）

球谐函数，是定义在球面上的基函数；
小波是一种在有限时间内振荡、能量快速衰减到零的数学函数，小波具有局部性，能同时分析信号的时间（空间）和频率信息.

小波是一系列基函数，定义在2D图像上，可以认为是一个个小的图像块，不同的小波定义域不同.

如下图，是2D哈尔小波（Haar Wavelet）：

img

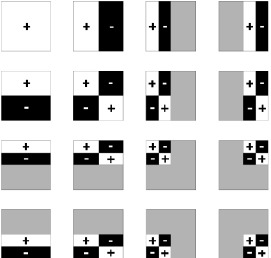
小波函数通过母小波（Mother Wavelet）ψ(t)生成：

\[ψ_{a,b}(t)=\frac{1}{\sqrt{a}}ψ(\frac{t-b}{a}) \]

其中，a 缩放因子（控制频率），b 平移因子（控制位置）.

小波变换（Wavelet Transform）是将信号分解为不同频率成分的数学工具.

与SH最大区别：
小波支持全频率表示，而小波只支持低频表示.

小波缺点：
不支持快速旋转.

参考

Games202 Lecture 5

计算机图形学【GAMES-101】2、光栅化(反走样、傅里叶变换、卷积)

posted @ 2025-06-12 10:49  明明1109  阅读(83)  评论(0)    收藏  举报