几何体变换到屏幕一般步骤:

MVP变换:模型(Model)、视图(View)、投影(Projection)变换这3个变换的集合的简称.
坐标空间变换流程:
\[\begin{aligned}
& Object \ Space\xrightarrow{Model}World\ Space\xrightarrow{Camera/View}Camera \ Space/View \ Space \\
& \xrightarrow{Perspective}Clip \ Space\xrightarrow{Perspective\ Divide}NDC \xrightarrow{viewport}Screen \ Space
\end{aligned}
\]
对应坐标变换流程:
\[\begin{aligned}
& v(x,y,z)\to v(x,y,z,1)\xrightarrow{Model} v_{world}(x,y,z,1) \xrightarrow{Camera/View} v_{camera}(x,y,z,1) \\
& \xrightarrow{Perspective} v_{clip}(x,y,z,w) \xrightarrow{Perspective\ Divide} v_{ndc}(x/w,y/w,z/w) \xrightarrow{viewport}v_{screen}(x,y)
\end{aligned}
\]
模型变换
模型变换(Model Transformation):在xyz世界坐标系下,变换几何体的几何属性.
主要包括操作:
- 平移(translate):将物体移动到指定位置;
- 缩放(scale):进行x轴、y轴、z轴方向的缩放;
- 旋转(rotate):绕指定轴(轴向量\(\bm{axis}\))旋转一定角度.
于是,模型变换矩阵:
\[M_{modeling} = T(x_0, y_0, z_0) * R(\bm{axis}, \theta) * S(s.x, s.y, s.z)
\]
通常由用户指定平移位置、缩放系数、旋转轴以及旋转角度.
视图变换
视图变换(View Transformation):又称相机变换(Camera Transformation),世界坐标系下的几何体,可能需要改变观察点、观察方向,而得到不同观察结果. 为此,需要将几何体变换到uvw观察坐标系下.
为确定观察者位置、朝向,用户通常需要指定:
- 眼睛位置\(\bm{e}\)
- 观察方向\(\bm{g}\)
- (初始的)观察向上向量\(\bm{t}\)
\(\bm{e},\bm{g},\bm{t}\)与uvw观察坐标系(符合右手定则)的关系:
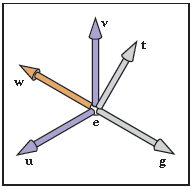
其中,\(\bm{e},\bm{g},\bm{t}\)由用户指定;\(\bm{t}\)是和\(\bm{g},\bm{v}\)共面的任意向量;\(\bm{w}=\bm{n}=-\bm{g}\)
对于任意视图,需要将物体从xyz坐标系(世界坐标系)变换到uvw坐标系(观察坐标系):
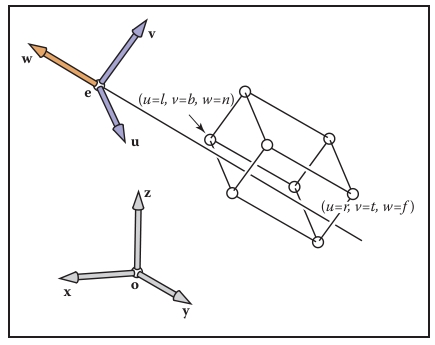
注:观察坐标系下,\(\bm{u},\bm{v},\bm{w}\)也分别对应另一种叫法\(\bm{x_{view}},\bm{y_{view}},\bm{z_{view}}\). \(\bm{v}\)是实际的观察向上向量.
如何根据用户指定\(\bm{e},\bm{g},\bm{t}\)构造uvw坐标系?
构造方式如下:
\[\begin{aligned}
\bm{w} &= -\frac{\bm{g}}{|\bm{g}|}\\
\bm{u} &= \frac{\bm{t}\times \bm{w}}{|\bm{t}\times \bm{w}|}\\
\bm{v} &= \bm{w} \times \bm{u}
\end{aligned}
\]
如何将\(xyz\)系统一点\(P\)转换到\(uvw\)系统的点\(P'\)?
\(xyz\)坐标系、\(uvw\)坐标系,都是由一组规范正交基为坐标轴建立的笛卡尔坐标系. 计算机图形:三维坐标系变换中提到,坐标轴与点变换对应关系:
\[uvw坐标轴\xrightarrow{R\cdot T}xyz坐标轴\\
P\xrightarrow{R\cdot T}P'
\]
设\(uvw\)原点(即视点\(\bm{e}\))在\(xyz\)系统下坐标\(\bm{e}(x_0,y_0,z_0)^{xyz}\),那么相机变换矩阵为:
\[M_{camera}=\begin{pmatrix}u_x&u_y&u_z&-\bm{u}\cdot\bm{e}\\
v_x&v_y&v_z&-\bm{v}\cdot \bm{e}\\
w_x&w_y&w_z&-\bm{w}\cdot \bm{e}\\
0&0&0&1\end{pmatrix}
\]
其中,\(u(u_x,u_y,u_z),v(v_x,v_y,v_z),w(w_x,w_y,w_z)\)是\(u,v,w\)轴单位向量,可根据前面方法算出.
投影变换
投影变换(Projective Transformations)分为两种:
- 正交投影;
- 透视投影.
观察坐标系下,为了简化公式,对投影观察体的边界作如下简记:
\[\begin{aligned}
xw_{min} &= l : left plane,\\
xw_{max} &= r : right plane,\\
yw_{min} &= b : bottom plane,\\
yw_{max} &= t : top plane,\\
z_{near} &= n : near plane,\\
z_{far} &= f : far plane.
\end{aligned}
\]
注:\(z_{near}, z_{far}\)分别代表观察体的近、远平面的z坐标值,且\(z_{far} < z_{near} <0\).
注意:投影变换矩阵,一定是依赖于我们的投影模型,不能脱离变换模型单论投影变换. 例如,\(n,f\)的符号,齐次参数(h=z,or -z),规范化观察体(什么样的立方体,左手or右手坐标系). 如果发现变换矩阵看不懂,那一定是模型没讲清楚.
正交投影变换
正交投影(Orthographic Projection):将物体沿与投影平面法向量平行的方向,变换到观察平面上的过程.
观察坐标系下,直线段\(P_1P_2\)正交投影到观察平面上的\(P_1'P_2'\):
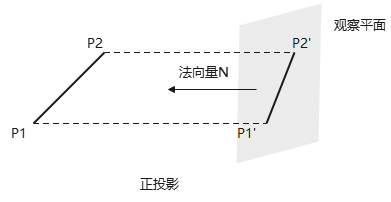
由于观察的内容不是无限的,通过选定远、近平面 + 裁剪窗口的边界的投影线,构成了正交投影观察体:
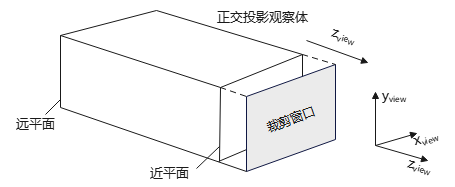
注:裁剪窗口所在平面,就是投影平面.
OpenGL中的正交投影
规范化变换:
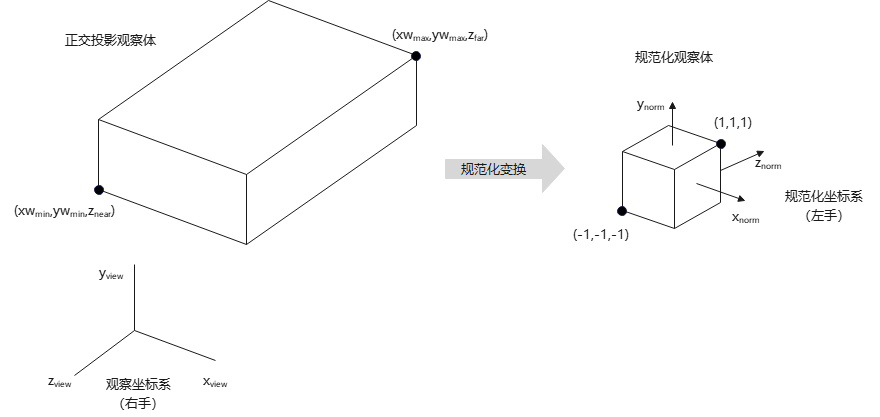
理论上,正交投影与规范化是分开的,但实际应用常将二者放到一个投影变换中.
于是,正交投影变换矩阵(正交投影 + 规范化):
\[\begin{aligned}
M_{ortho,norm}&=\begin{pmatrix}
\frac{2}{xw_{max}-xw_{min}} & 0 & 0 & -\frac{xw_{min}+xw_{max}}{xw_{max}-xw_{min}}\\
0 & \frac{2}{yw_{max}-yw_{min}} & 0 & -\frac{yw_{min}+yw_{max}}{yw_{max}-yw_{min}}\\
0 & 0 & -\frac{2}{z_{near}-z_{far}} & \frac{z_{near}+z_{far}}{z_{near}-z_{far}}\\
0& 0 & 0 & 1
\end{pmatrix}\\
&=\begin{pmatrix}
\frac{2}{r-l} & 0 & 0 & -\frac{r+l}{r-l}\\
0 & \frac{2}{t - b} & 0 & -\frac{t + b}{t - b}\\
0 & 0 & -\frac{2}{n - f} & \frac{n+f}{n-f}\\
0 & 0 & 0 & 1
\end{pmatrix}
\\
\end{aligned}
\]
注:
1)这里观察坐标系是右手系统,NDC是左手系统(z轴反射变换,决定了\(M_{33}=-\frac{2}{n-f}\)的负号);
2)裁剪窗口关于\(z_{view}\)轴对称.
推导过程参见:计算机图形:三维观察之投影变换正投影部分.
Games101中的正交投影
Games101跟我们得出的投影矩阵不一样,因为其规范化坐标系(NDC)是右手系统,而非左手系统,没有对z轴进行反射.
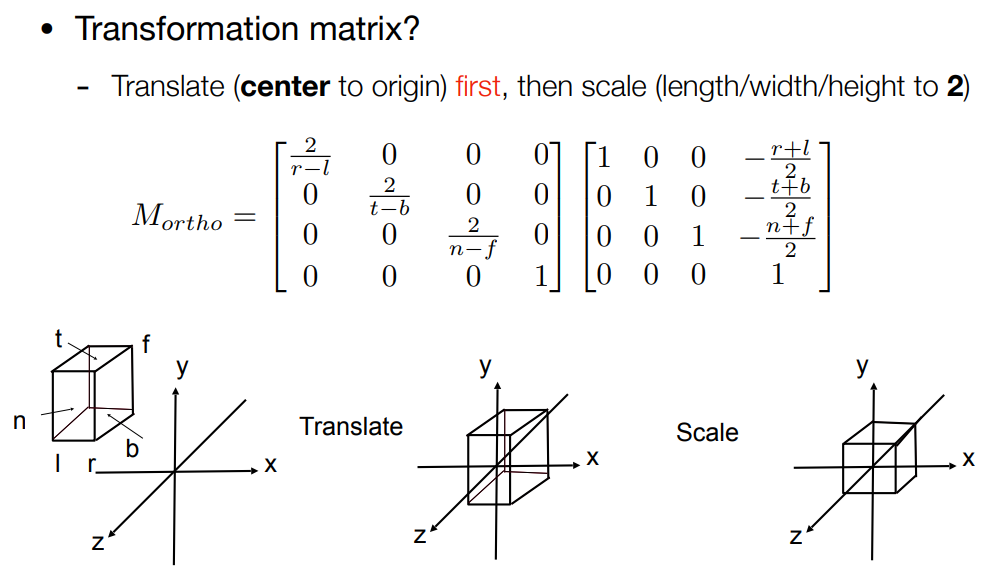
from Games101 Lecture04
如上图,
\[\begin{aligned}
M_{ortho} &= \begin{pmatrix}
\frac{2}{r-l} & 0 & 0 & 0\\
0 & \frac{2}{t-b} & 0 & 0\\
0 & 0 & \frac{2}{n-f} & 0\\
0 & 0 & 0 & 1
\end{pmatrix}\cdot \begin{pmatrix}
1 & 0 & 0 & -\frac{r+l}{2}\\
0 & 1 & 0 & -\frac{t+b}{2}\\
0 & 0 & 1 & -\frac{n+f}{2}\\
0 & 0 & 0 & 1
\end{pmatrix}\\
&= \begin{pmatrix}
\frac{2}{r-l} & 0 & 0 & -\frac{r+l}{r-l}\\
0 & \frac{2}{t-b} & 0 & -\frac{t+b}{t-b}\\
0 & 0 & \frac{2}{n-f} & -\frac{n+f}{n-f}\\
0 & 0 & 0 & 1
\end{pmatrix}
\end{aligned}
\]
透视投影
透视投影(Perspective Projection):将物体沿会聚到投影参考点(projection reference point)的路径,投影到观察平面,来逼近几何光学效果的过程.
观察坐标系下,点\(P\)透视投影到观察平面上的点\(P'\):
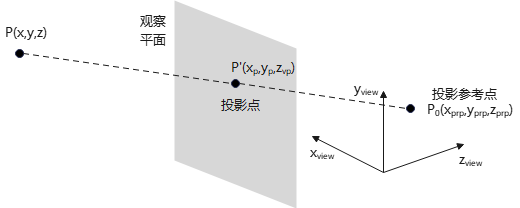
OpenGL中的透视投影
为了简化模型,
- 将投影参考点固定到观察原点,即\(P_0(x_{prp},y_{prp},z_{prp})=(0,0,0)\);
- 将近平面作为观察平面,即\(z_{vp} = z_{near}\);
- 投影窗口选成关于\(z_{view}\)轴对称,那么\(xw_{max} = -xw_{min}, yw_{max} = -yw_{min}\),即\(r = -l, t = -b\)
于是,简化的透视投影变换矩阵(透视投影 + 规范化)为:
\[\begin{aligned}
M_{pers, norm} &= \begin{pmatrix}
\frac{-2z_{near}}{xw_{max}-xw_{min}}
& 0 & \frac{xw_{min}+xw_{max}}{xw_{max}-xw_{min}} & 0\\
0 & \frac{-2z_{near}}{yw_{max}-yw_{min}} & \frac{yw_{min}+yw_{max}}{yw_{max}-yw_{min}} & 0\\
0 & 0 & \frac{z_{near}+z_{far}}{z_{near}-z_{far}} & \frac{-2z_{near}z_{far}}{z_{near}-z_{far}}\\
0 & 0 & -1 & 0
\end{pmatrix}\\
& = \begin{pmatrix}
\frac{-2n}{r - l} & 0 & \frac{r + l}{r - l} & 0\\
0 & \frac{-2n}{t - b} & \frac{t + b}{t - b} & 0\\
0 & 0 & \frac{n + f}{n - f} & \frac{-2nf}{n - f}\\
0 & 0 & -1 & 0
\end{pmatrix}\\
& = \begin{pmatrix}
\frac{-2n}{r - l} & 0 & 0 & 0\\
0 & \frac{-2n}{t - b} & 0 & 0\\
0 & 0 & \frac{n + f}{n - f} & \frac{-2nf}{n - f}\\
0 & 0 & -1 & 0
\end{pmatrix},(h=-z)
\end{aligned}
\]
注意:
1)\(r,l,t,b\)是裁剪窗口的边界,\(n,f\)是远近平面的z坐标;
2)有的文献中,\(M_{pers, norm}[4:3]=1\)而不是-1,这是因为选的齐次参数\(h=z\),而不是文中的\(h=-z\),并不会影响点\(P(x,y,z)\)投影后的点\(P'(x',y',z')\)坐标.
ref. P153 Marschner S , Shirley P. Fundamentals of computer graphics. 4th edition.
思考: 透视变换后,点已经限制在规范化观察体\([-1,1]^3\)内,为什么还需要做透视除法?
因为此时点是4D点,最后一个维度\(w(-z\le w\le z)\)并没有消除,需要将其转换为3D点\((x/w,y/w,z/w)\),即投影到\(w=1\)对应的空间上.
透视投影的几何含义可参见tinyrenderer笔记:透视投影
透视矩阵还有另一种表示方式,即用FOV+aspect表示,而不用裁剪窗口边界.
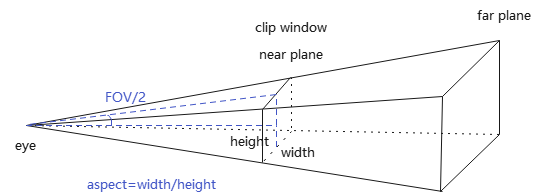
\[tan \frac{FOV}{2}=\frac{height/2}{n},\\
aspect=\frac{width}{height}
\]
裁剪窗口的边界与尺寸关系:
\[height=t-b,width=r-l
\]
∴
\[n=-\frac{height}{2tan \frac{FOV}{2}}=-\frac{width}{aspect\cdot 2tan\frac{FOV}{2}}
\]
注意:\(n=near=z_{near}<0\)
∴投影矩阵也可写成用FOV+aspect表示形式:
\[M_{pers,norm}=\begin{pmatrix}
\frac{1}{aspect\cdot tan\frac{FOV}{2}} & 0 & 0 & 0\\
0 & \frac{1}{tan \frac{FOV}{2}} & 0 & 0\\
0 & 0 & \frac{n+f}{n-f} & -\frac{2nf}{n-f}\\
0 & 0 & -1 & 0
\end{pmatrix}
\]
ref. Doanald Hearn.计算机图形学:(第四版)[M].电子工业出版社,2014.
Games101中的透视投影
Games101中的透视投影,分为2步进行:
1)将棱台观察体压扁,变换成长方体
原则:n->n,f->f保持不变. 对应变换矩阵\(M_{persp\to ortho}\)
2)正交投影,即将上面长方体规范化到\([-1,1]^3\)的立方体
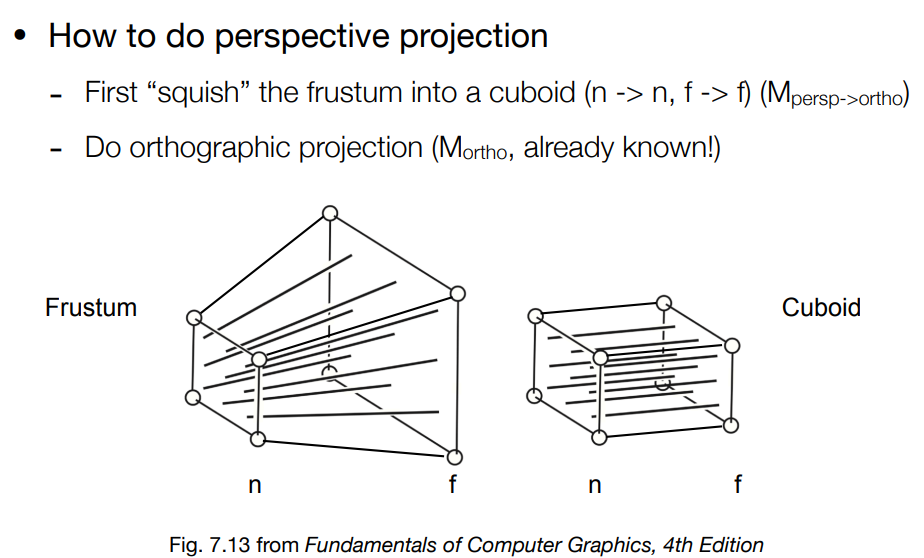
对于1),如何将观察体压扁?
可以通过将\(P(x,y,z)\)投影到近平面\(P'(x',y',z')\),从而找到投影变换关系
\[\begin{aligned}
y'&=\frac{n}{z}y,\\
x'&=\frac{n}{z}x(similar\space to\space y')
\end{aligned}
\]

于是,可得到粗略的投影变换(齐次坐标):
\[\begin{pmatrix}
x\\y\\z\\1
\end{pmatrix}
\xrightarrow{M_{persp\to ortho}}\begin{pmatrix}
x'\\y'\\z'\\1
\end{pmatrix}=\begin{pmatrix}
\frac{n}{z}x\\\frac{n}{z}y\\?\\1
\end{pmatrix}
\]
由透视投影的几何意义(参见tinyrenderer笔记:透视投影),我们知道\((x,y,z,1),(kx,ky,kz,k\neq 0),(zx,zy,z^2,z\neq 0)\)投影到\(w=1\),都表示同一个投影点,即它们是等效的.
有
\[\begin{pmatrix}
\frac{n}{z}x\\\frac{n}{z}y\\?\\1
\end{pmatrix}
\xLeftrightarrow{mult. \space by\space z} \begin{pmatrix}
nx\\ny\\?\\z
\end{pmatrix}
\]
∴\(M_{persp\to ortho}\)需满足:
\[\begin{pmatrix}nx\\ny\\?\\z\end{pmatrix}
=M_{persp\to ortho}
\begin{pmatrix}x\\y\\z\\1\end{pmatrix}
\]
∴可构造出
\[M_{persp\to ortho}=\begin{pmatrix}
n & 0 & 0 & 0\\
0 & n & 0 & 0\\
? & ? & ? & ?\\
0 & 0 & 1 & 0
\end{pmatrix}
\]
由于从frustum压扁成长方体过程中,
(1) 近平面上任一点不会改变;
(2) 远平面上任一点的z值不会改变.
∴由(1)
\[\begin{pmatrix}nx\\ny\\n^2\\n\end{pmatrix}
=M_{persp\to ortho}
\begin{pmatrix}x\\y\\n\\1\end{pmatrix}
\]
∴\(M_{persp\to ortho}\)第三行必须是\(\begin{pmatrix}0 & 0 & A & B\end{pmatrix}\)的形式(∵\(n^2\)与x,y项无关)
∴\(n^2=\begin{pmatrix}0 & 0 & A & B\end{pmatrix}\begin{pmatrix}x\\y\\n\\1\end{pmatrix}\)
∴\(n^2=An+B\)
由(2),远平面上任一点z值不变,不妨取\(\begin{pmatrix}0 & 0 & f & 1\end{pmatrix}\),
其等价点\(\begin{pmatrix}0 & 0 & f^2 & f\end{pmatrix}\)
∴
\[\begin{pmatrix}0 \\ 0 \\ f^2 \\ f\end{pmatrix}=M_{persp\to ortho}\begin{pmatrix}0 \\ 0 \\ f \\ 1\end{pmatrix}\\
\therefore f^2=\begin{pmatrix}0 & 0 & A & B\end{pmatrix}\begin{pmatrix}0 \\ 0 \\ f \\ 1\end{pmatrix}\\
\therefore f^2 = Af+B
\]
联立2个方程,可解得:
\[A=n+f,B=-nf
\]
于是,
\[M_{persp\to ortho}=\begin{pmatrix}
n & 0 & 0 & 0\\
0 & n & 0 & 0\\
0 & 0 & n+f & -nf\\
0 & 0 & 1 & 0
\end{pmatrix}
\]
对应坐标变换为
\[\begin{pmatrix}x\\y\\z\\1\end{pmatrix}\xrightarrow{M_{persp\to ortho}}\begin{pmatrix}nx\\ny\\(n+f)z-nf\\z\end{pmatrix}\xLeftrightarrow{div. w=z}
\begin{pmatrix}
nx/z\\
ny/z\\
n+f-nf/z\\
1
\end{pmatrix}
\]
注意:这里的齐次参数是\(h=z\),当然如果选择\(h=-z\)(对应变换矩阵同步也需要修改),但不影响最终的投影点坐标(3D),因为最终都会投影到\(w=1\)的空间(齐次除法).
至此,第1)步已完成,考虑第2)步 正交投影.
\[M_{ortho}=\begin{pmatrix}
\frac{2}{r-l} & 0 & 0 & -\frac{r+l}{r-l}\\
0 & \frac{2}{t-b} & 0 & -\frac{t+b}{t-b}\\
0 & 0 & \frac{2}{n-f} & -\frac{n+f}{n-f}\\
0 & 0 & 0 & 1
\end{pmatrix}
\]
∴最终的透视投影矩阵
\[\begin{aligned}
M_{persp} &= M_{ortho}M_{persp\to ortho}\\
&= \begin{pmatrix}\frac{2}{r-l} & 0 & 0 & -\frac{r+l}{r-l}\\
0 & \frac{2}{t-b} & 0 & -\frac{t+b}{t-b}\\
0 & 0 & \frac{2}{n-f} & -\frac{n+f}{n-f}\\
0 & 0 & 0 & 1\end{pmatrix}
\cdot \begin{pmatrix}
n & 0 & 0 & 0\\
0 & n & 0 & 0\\
0 & 0 & n+f & -nf\\
0 & 0 & 1 & 0
\end{pmatrix}\\
&=\begin{pmatrix}
\frac{2n}{r-l} & 0 & \frac{l+r}{l-r} & 0\\
0 & \frac{2n}{t-b} & \frac{b+t}{b-t} & 0\\
0 & 0 & \frac{f+n}{n-f} & -\frac{2nf}{n-f}\\
0 & 0 & 1 & 0
\end{pmatrix}(h=z)
\end{aligned}
\]
见P153 Fundamentals of Computer Graphics-4th.
该变换会将n映射到1,f映射到-1. 也就是说,没有将z轴反射,规范化坐标系还是右手系.
举例验证,设近平面一点\(p_1=(x_1,y_1,n,1)^T\),远平面一点\(p_2=(x_2,y_2,f,1)^T\)
由于只关心n、f映射,所以只需要计算z、w值:
\[\begin{aligned}
M_{persp}p_1 &= \begin{pmatrix}
- & 0 & - & 0\\
0 & - & - & 0\\
0 & 0 & \frac{f+n}{n-f} & -\frac{2nf}{n-f}\\
0 & 0 & 1 & 0
\end{pmatrix}\begin{pmatrix}x_1\\y_1\\n\\1\end{pmatrix}\\
&= \begin{pmatrix}-\\-\\n\frac{f+n}{n-f}-\frac{2nf}{n-f}\\n\end{pmatrix}\\
&= \begin{pmatrix}-\\-\\n\\n\end{pmatrix}\xLeftrightarrow{div.w=n}\begin{pmatrix}-\\-\\1\\1\end{pmatrix}
\end{aligned}
\]
类似地,
\[\begin{aligned}
M_{persp}p_2 &= \begin{pmatrix}-\\-\\-f\\f\end{pmatrix}
\end{aligned}\xLeftrightarrow{div.w=f}\begin{pmatrix}-\\-\\-1\\1\end{pmatrix}
\]
RTR 4th中的透视投影
Real-Time Rendering 4th edition - Tomas(以下简称RTR 4th)中,描述了一个透视投影矩阵,跟Games101的透视投影矩阵很像,但是第三行符号相反,这是为什么?
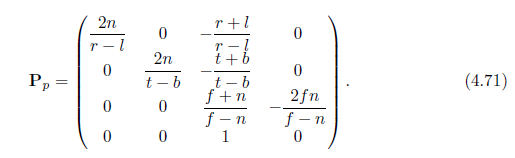
from P98 RTR 4th
前面提到,Games101中,规范化立方体并非标准的左手系统,而是与观察坐标系相同的右手系统(\(n\to 1, f\to -1\)).
如果在Games101中的\(M_{persp}\)基础上,再加上沿z轴的反射(坐标点z值大小不变,符号相反),相当于绕z轴旋转180°
\[M_{zreflect}=\begin{pmatrix}
1 & 0 & 0 & 0\\
0 & 1 & 0 & 0\\
0 & 0 & -1 & 0\\
0 & 0 & 0 & 1
\end{pmatrix}
\]
注:有的地方理解成沿z轴的放缩\(S(1,1,-1,1)\). 不管何种理解,变换矩阵是相同的即可.
参见:计算机图形:特殊几何变换 三维反射
于是,可得新的透视投影变换矩阵(左手系统),与RTR 4th中的\(P_p\)完全一致:
\[\begin{aligned}
M_{zreflect}M_{persp} &= \begin{pmatrix}
1 & 0 & 0 & 0\\
0 & 1 & 0 & 0\\
0 & 0 & -1 & 0\\
0 & 0 & 0 & 1
\end{pmatrix}
\cdot \begin{pmatrix}
\frac{2n}{r-l} & 0 & \frac{l+r}{l-r} & 0\\
0 & \frac{2n}{t-b} & \frac{b+t}{b-t} & 0\\
0 & 0 & \frac{f+n}{n-f} & -\frac{2nf}{n-f}\\
0 & 0 & 1 & 0
\end{pmatrix}\\
&= \begin{pmatrix}
\frac{2n}{r-l} & 0 & \frac{l+r}{l-r} & 0\\
0 & \frac{2n}{t-b} & \frac{b+t}{b-t} & 0\\
0 & 0 & -\frac{f+n}{n-f} & \frac{2nf}{n-f}\\
0 & 0 & 1 & 0
\end{pmatrix}\\
&= P_p
\end{aligned}
\]
此时,\(n\to -1, f\to 1\)
通常,渲染管线会将远平面以外的物体裁剪掉,而有的应用中,需要远平面f取为无穷远,例如使用了天空盒,但规范化同样需要\(n\to -1, f\to 1\)
\[\begin{aligned}
P_p &= \begin{pmatrix}
\frac{2n}{r-l} & 0 & \frac{l+r}{l-r} & 0\\
0 & \frac{2n}{t-b} & \frac{b+t}{b-t} & 0\\
0 & 0 & \lim\limits_{f\to -∞}-\frac{f+n}{n-f} & \lim\limits_{f\to -∞}\frac{2nf}{n-f}\\
0 & 0 & 1 & 0
\end{pmatrix}\\
&= \begin{pmatrix}
\frac{2n}{r-l} & 0 & \frac{l+r}{l-r} & 0\\
0 & \frac{2n}{t-b} & \frac{b+t}{b-t} & 0\\
0 & 0 & 1 & -2n\\
0 & 0 & 1 & 0
\end{pmatrix}
\end{aligned}
\]
有的渲染管线(API)如DirectX,可能将n平面映射到\(z=0\)(不再是\(z=-1\)),f平面映射到\(z=1\).
之前的规范化观察体,是立方体\([-1,1]\times[-1,1]\times[-1,1]\);现在,是长方体\([-1,1]\times [-1,1]\times [0,1]\)
也就是说,先z轴方向右移1(\([-1,1]\to[0,2]\)),然后放缩0.5(\([0,2]\to [0,1]\))
\[T(0,0,1,0)=\begin{pmatrix}
1 & 0 & 0 & 0\\
0 & 1 & 0 & 0\\
0 & 0 & 1 & 1\\
0 & 0 & 0 & 1
\end{pmatrix}\\
S(1,1,0.5,1)=\begin{pmatrix}
1 & 0 & 0 & 0\\
0 & 1 & 0 & 0\\
0 & 0 & 0.5 & 0\\
0 & 0 & 0 & 1
\end{pmatrix}
\]
∴
\[\begin{aligned}
M_{st} &=S(1,1,0.5,1)T(0,0,1,0)\\
&=\begin{pmatrix}
1 & 0 & 0 & 0\\
0 & 1 & 0 & 0\\
0 & 0 & 0.5 & 0.5\\
0 & 0 & 0 & 1
\end{pmatrix}
\end{aligned}
\]
∴
\[\begin{aligned}
P_{p[0,1]} &=M_{st}P_p\\
&=\begin{pmatrix}
1 & 0 & 0 & 0\\
0 & 1 & 0 & 0\\
0 & 0 & 0.5 & 0.5\\
0 & 0 & 0 & 1
\end{pmatrix}
\cdot \begin{pmatrix}
\frac{2n}{r-l} & 0 & \frac{l+r}{l-r} & 0\\
0 & \frac{2n}{t-b} & \frac{b+t}{b-t} & 0\\
0 & 0 & -\frac{f+n}{n-f} & \frac{2nf}{n-f}\\
0 & 0 & 1 & 0
\end{pmatrix}\\
&= \begin{pmatrix}
\frac{2n}{r-l} & 0 & \frac{l+r}{l-r} & 0\\
0 & \frac{2n}{t-b} & \frac{b+t}{b-t} & 0\\
0 & 0 & -\frac{f}{n-f} & \frac{nf}{n-f}\\
0 & 0 & 1 & 0
\end{pmatrix}
\end{aligned}
\]
透视投影的另类理解
前面,我们从视景体的投影变换、规范化变换,是正向一步步推导出透视投影矩阵. Real-time Rendering 4th中提到另一种透视投影矩阵,更加直观更容易理解.
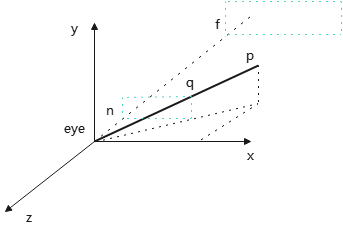
如上图,设视景体中任一点\(p(p_x,p_y,p_z)\),我们将其投影到近平面\(z=-d,d>0\),\(n=-d\). 要求\(f<n<0\)
那么,会产生投影点\(q(q_x,q_y,-d)(q_z=-d)\)
根据三角形相似性,有
\[\frac{q_x}{p_x}=\frac{-d}{p_z}\iff q_x=-d\frac{p_x}{p_z}
\]
同理,
\[q_y=-d\frac{p_y}{p_z}
\]
那么,透视投影矩阵:
\[P_p=\begin{pmatrix}
1 & 0 & 0 & 0\\
0 & 1 & 0 & 0\\
0 & 0 & 1 & 0\\
0 & 0 & -1/d & 0
\end{pmatrix}
\]
为什么跟我们前面的\(M_{pers,norm}\)不太一样?是不是能起到透视投影的作用?
答:它们是等效的,但不相等. 下面进行说明.
我们用\(P_p\)对p点变换:
\[\begin{aligned}
P_pp &= \begin{pmatrix}
1 & 0 & 0 & 0\\
0 & 1 & 0 & 0\\
0 & 0 & 1 & 0\\
0 & 0 & -1/d & 0
\end{pmatrix}
\begin{pmatrix}p_x\\p_y\\p_z\\1\end{pmatrix}\\
&=\begin{pmatrix}p_x\\p_y\\p_z\\-p_z/d \end{pmatrix}
\xRightarrow{div. w=-p_z/d}\begin{pmatrix}-dp_x/p_z\\-dp_y/p_z\\-d\\1 \end{pmatrix}
=\begin{pmatrix}q_x\\q_y\\q_z\\1\end{pmatrix}=q
\end{aligned}
\]
也就是说,\(P_pp\)得到的是与q点等效点,但还需要做透视除法(\(w=-p_z/d\)),即将点投影到\(w=1\)的空间,才得到q点. 其中,齐次参数\(h=w\)
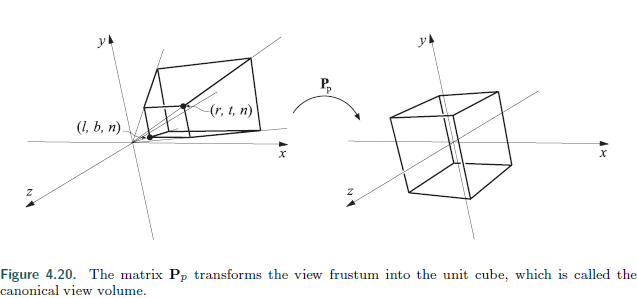
如下图所示,因为裁剪窗口是有个有限的空间,所以视景体(由所有能投影到裁剪窗口的点组成)也是一个有限空间.
设z=n平面上,最小角点\((l,b,n)\),最大角点\((r,t,f)\). 参数\((l,r,b,t,n,f)\)决定了相机的视景体(frustum).
left, right plane => horizontal FOV;
bottom, top plane => vertical FOV
FOV值越大,相机能看到的角度范围越广.
小结
不管我们的透视变换是什么样,最终都是要将视景体内任一点,投影到近平面,然后做齐次除法,最终得到规范化立方体.
参考
- Marschner S , Shirley P .Fundamentals of computer graphics. 4th edition.[J].World Scientific Publishers Singapore, 2009, 9(1):29-51.DOI:doi:10.1021/i160033a008.
- 计算机图形:三维观察之投影变换
- Homogeneous Coordinates, Clip Space, and NDC | WebGPU











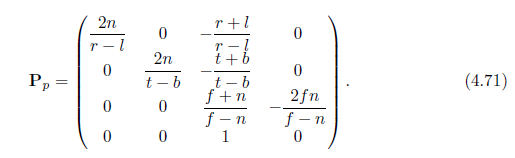




 浙公网安备 33010602011771号
浙公网安备 33010602011771号