将对象的描述从一个坐标系转换到另一个,在图形应用非常重要。本文主要从坐标的角度,探讨二维、三维空间下的对象如何从一个坐标系转换到另一个坐标系。
坐标系:除了笛卡尔坐标系,有极坐标、球面坐标、椭圆坐标等。这里仅考虑笛卡尔坐标系。
二维坐标系变换
由旋转角进行坐标系转换
坐标轴的正交变换:
\[\delta: A[\bm{e_1},\bm{e_2};O(0,0)]\xrightarrow{\begin{aligned}&1. 绕O逆时针旋转θ;\\&2. 平移至O'(x_0,y_0)\end{aligned}}B[\bm{e_1'},\bm{e_2'};O'(x_0,y_0)]
\]
其中,\(\bm{e_1}=(1,0)^A,\bm{e_2=}(0,1)^A\)是A的基向量;\(\bm{e_1'}=(1,0)^B,\bm{e_2'}=(0,1)^B\)是B的基向量.
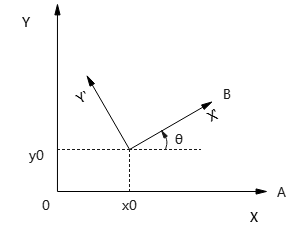
含义:2D空间下,2个坐标系:A为\(xy\)坐标系,B为\(x'y'\)坐标系。其中,\(xy\)系统原点\(O(0,0)^A\),将其绕原点逆时针旋转θ角,然后平移至\(O'(x_0,y_0)^A\)处,得到\(x'y'\)坐标系。
tips:A系统下坐标,记为\((x,y)^A\);B系统下坐标,记为\((x,y)^B\). 如果不注明,默认是A系统坐标.
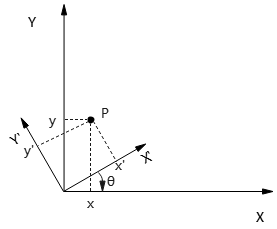
问题:A系统任一点\(P(x,y)^A\),如何转换到B系统的点\(P'(x', y')^B\)?
点的坐标转换与坐标轴的转换,方向相反,即
\[P\xrightarrow{复合变换M} P'\iff B \xrightarrow{复合变换M} A
\]
于是,可分两步得到复合变换矩阵M:
- T: 将\(O'(x_0,y_0)\)平移到\(O(0,0)\);
- R: 将\(x'\)轴顺时针旋转\(θ\)角与x轴重合。
步骤1平移矩阵:
\[\tag{1}
T(-x_0,-y_0)=\begin{bmatrix}
1 & 0 & -x_0\\
0 & 1 & -y_0\\
0 & 0 & 1
\end{bmatrix}
\]
步骤2旋转矩阵:
\[\tag{2}
R_z(-θ)=\begin{bmatrix}
\cosθ & \sinθ & 0\\
-\sinθ & \cosθ & 0\\
0 & 0 & 1
\end{bmatrix}
\]
注意:顺时针旋转取\(-θ\)。
于是,\(P(x,y)\xrightarrow{M_{xy,x'y'}} P'(x',y')\)的复合变换矩阵:
\[\tag{3}
\begin{aligned}
M_{xy,x'y'}&=R_z(-θ)\cdot T(-x_0,-y_0)\\
&=
\begin{bmatrix}
\cosθ & \sinθ & 0\\
-\sinθ & \cosθ & 0\\
0 & 0 & 1
\end{bmatrix}
\cdot
\begin{bmatrix}
1 & 0 & -x_0\\
0 & 1 & -y_0\\
0 & 0 & 1
\end{bmatrix}
\\
&=\begin{bmatrix}
\cosθ & \sinθ & -(x_0\cosθ+y_0\sinθ)\\
-\sinθ & \cosθ & x_0\sinθ-y_0\cosθ\\
0 & 0 & 1
\end{bmatrix}
\end{aligned}
\]
这样,A系统坐标通过平移、旋转,得到B系统坐标。
思考:上述复合变换中,明明\(x'y'\)坐标轴变换成了\(xy\)坐标轴,为什么\(xy\)系统转换成\(x'y'\)系统,而不是反过来?
用最简单的点\((0,0)\)来验证。假设\(x'y'\)系统下,原点坐标\((0,0)^B\),那么在\(xy\)系统下坐标为\((x_0,y_0)^A\),显然不符合复合变换;
而\(xy\)系统原点\((0,0)^A\),在\(x'y'\)系统下,坐标为\((-(x_0\cosθ+y_0\sinθ),x_0\sinθ-y_0\cosθ)^B\),符合复合变换。
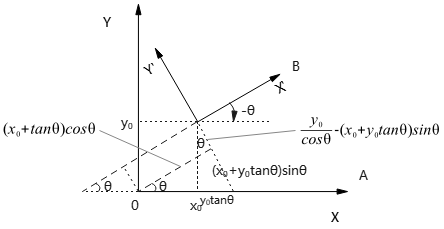
求解\(O(0,0)^A\)在B系统下坐标示意图(注意加负号):
经复合变换,\(P(x_p,y_p)^A\to P'(x_p',y_p')^B\)。
变换过程:
\[P'(x_p',y_p')^B=M_{xy,x'y'}P(x_p,y_p)^A=R_z(-θ)\cdot T(-x_0,-y_0)\cdot \begin{bmatrix}
x_p\\y_p\\1
\end{bmatrix}^A
\]
令\(x=x_p, y=y_p, x'=x_p', y'=y_p'\),
那么,
\[\tag{4}
P'(x',y')^B=R_z(-θ)\cdot T(-x_0,-y_0)\cdot P(x,y)^A
\]
这样,就将\(xy\)系统坐标转换到了\(x'y'\)系统。
构造旋转矩阵
有时,我们并不知道旋转角θ值,而知道新的坐标轴方向(\(x',y'\)轴)。此时,可先求θ大小(向量点积),然后得到旋转矩阵. 这里要介绍另一种方法:构造旋转矩阵,该变换将坐标轴\(x'y'\)旋转到坐标轴\(xy\),即将A系统坐标转换为B系统坐标。
正交矩阵概念
先复习几个概念:
点积为0的两个或多个向量,称为正交向量。
假设向量\(V_1=(x_1,y_1), V_2=(x_2,y_2)\)是一组正交向量,则\(V_1\cdot V_2=x_1x_2+y_1y_2=0\)。
所谓正交向量,
如果矩阵A,满足\(\bm{A}^T\bm{A}=E\),则称A为正交矩阵。
对于正交矩阵,其行向量组(或列向量组)为单位向量且两两正交。这组行(或列)向量构成一个空间的基,称为规范正交基。
下面证明:
设A是一个列向量矩阵且为正交矩阵,\(A=(\bm{α_1},\bm{α_2},...,\bm{α_n})\),其中\(\bm{α_i}(i=1,2,...,n)\)为列向量. 那么,
\[\begin{aligned}
A^TA = \begin{bmatrix}
\bm{α_1}^T\\
\bm{α_2}^T\\
...
\bm{α_n}^T
\end{bmatrix}
\begin{bmatrix}
\bm{α_1},\bm{α_2},...,\bm{α_n}
\end{bmatrix} &= E\\
\begin{bmatrix}
\bm{α_1}^T\bm{α_1} & \bm{α_1}^T\bm{α_2} & ... & \bm{α_1}^T\bm{α_n}\\
\bm{α_2}^T\bm{α_1} & \bm{α_2}^T\bm{α_2} & ... & \bm{α_2}^T\bm{α_n}\\
... & ... & ... & ...\\
\bm{α_n}^T\bm{α_1} & \bm{α_n}^T\bm{α_2} & ... & \bm{α_n}^T\bm{α_n}
\end{bmatrix}&=\begin{bmatrix}
1 & 0 & ... & 0\\
0 & 1 & ... & 0\\
... & ... & ... & ...\\
0 & 0 & ... & 1
\end{bmatrix}
\end{aligned}
\]
对于任意列向量\(\bm{α_i}, \bm{α_j}\),
1)如果\(i=j\),那么\(\bm{α_i}*\bm{α_j}=\bm{α_i}*\bm{α_i}=1 \implies |\bm{α_i}|=1\);
2)如果\(i≠j\),那么\(\bm{α_i}*\bm{α_j}=0\),则\(\bm{α_i}, \bm{α_j}\)互为正交向量。
当A由行向量组成时,该结论依然成立。
利用正交矩阵构造旋转矩阵
已知向量\(\bm{V}\parallel y'\)轴,那么,\(y'\)轴单位向量:
\[\tag{5}
\bm{v} = {V\over |V|}=(v_x,v_y)^A
\]
将\(\bm{v}\)顺时针旋转90°,得到沿\(x'\)轴单位向量:
\[\tag{6}
\begin{aligned}
\bm{u} &= (u_x,u_y)\\
&=(v_y,-v_x)
\end{aligned}
\]
上式证明:
如下图
∵\(\bm{v}, \bm{u}\)都是单位向量
∴\(|\bm{v}|=|\bm{u}|=1\)
假设\(\bm{v}\)在第二象限,\(\bm{v}\)与y轴夹角\(α\)
∴\(\bm{v} = (-\cos α, \sin α), \bm{u} = (\sin α,\cos α)\)
∵\(\bm{v} = (v_x,v_y)\)
∴\(\bm{u}=(v_y,-v_x)\),即得证.
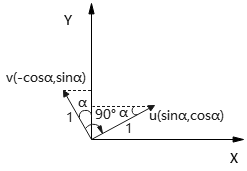
显然,\(\bm{v}, \bm{u}\)正交,即\(\bm{v}\cdot \bm{u}=0\iff v⊥u\)。
由(2)知,旋转矩阵\(R(-θ)\)的行向量组是一组正交单位向量(即一组规范正交基):
\[R(-θ)=\begin{bmatrix}
\cosθ & \sinθ & 0\\
-\sinθ & \cosθ & 0\\
0 & 0 & 1
\end{bmatrix}
\\
\]
i.e. 行向量组\((\cosθ, \sinθ, 0),(-\sinθ,\cosθ,0),(0,0,1)\)是一组规范正交基
问题:是否可以由一组规范正交基得到对应旋转矩阵?
答案是可以,可用规范正交基作为行向量(或列向量)组构造出旋转矩阵。不妨令,
\[\tag{7}
R=\begin{bmatrix}
u_x & u_y & 0\\
v_x & v_y & 0\\
0 & 0 & 1
\end{bmatrix}
\]
其中,\(v_x=-\sinθ,v_y=\cosθ\)。利用式(6)中\(\bm{u},\bm{v}\)的关系,可得\(u_x=v_y=\cosθ, u_y=-v_x=\sinθ\),这符合旋转矩阵\(R(-θ)\)特性。
tips: 行向量组\(\bm{u}=(u_x,u_y),\bm{v}=(v_x,v_y)\),对应左乘坐标(列向量)
\[\begin{aligned}
P' &= \begin{pmatrix}\bm{u}\\\bm{v}\\\end{pmatrix}P\\
\begin{pmatrix}x' \\ y'\end{pmatrix} &= \begin{pmatrix}\bm{u}\\\bm{v}\\\end{pmatrix}\begin{pmatrix}x \\ y\end{pmatrix}\\
\begin{pmatrix}x' \\ y'\end{pmatrix} &= \begin{pmatrix} xu_x+yu_y \\xv_x+yv_y \end{pmatrix}
\end{aligned}
\]
列向量组\(\bm{u}=\begin{pmatrix}u_x\\u_y\end{pmatrix},\bm{v}=\begin{pmatrix}v_x\\v_y\end{pmatrix}\),对应右乘坐标(行向量)
\[\begin{aligned}
P' &= P\begin{pmatrix}\bm{u} & \bm{v}\end{pmatrix}\\
\begin{pmatrix}x'&y'\end{pmatrix} &= \begin{pmatrix}x&y\end{pmatrix} \begin{pmatrix}\bm{u} & \bm{v}\end{pmatrix}\\
\begin{pmatrix}x' & y'\end{pmatrix} &= \begin{pmatrix}xu_x + yu_y \\ xv_x + yv_y\end{pmatrix}
\end{aligned}
\]
因此,旋转矩阵用行向量组,还是列向量组并无本质区别,可以看想变换的坐标用列向量形式,还是行向量形式.
接下来问题:\(θ\)在[0,2π)范围内是否有唯一解,即构造的旋转矩阵是否对应唯一的旋转?
答案是有唯一解。下面证明:
我们知道,正弦和余弦函数在0~2π范围内有2个解(如果有解),设2个解分别为\(θ_1,θ_2\in [0,2\pi)\)。
先根据\(\sinθ\)讨论\(θ\)取值范围,
1)当\(v_x<0\)时,\(\sinθ > 0\),那么\(θ_1 \in [0,{\pi\over 2}), θ_2\in [{\pi\over 2}, \pi)\);
2)当\(v_x\ge 0\)时,\(\sinθ \le 0\),那么\(θ_1\in [\pi,{3\over 2}\pi), θ_2\in[{3\over 2}\pi, 2\pi)\);
再根据\(\cosθ\)讨论\(θ\)取值范围,
1)当\(v_y>0\),则\(θ_1\in[0,{\pi\over 2}),θ_2\in[{3\over 2}\pi, 2\pi)\);
2)当\(v_y<0\),则\(θ_1\in [{\pi\over 2},\pi),θ_2\in [\pi,{3\over 2}\pi)\)。
再综合sin、cos取值范围。不难发现,当sin、cos取值确定时,\(θ\)范围只能是长度为π/2的4个区间之一:\([0,{\pi \over 2}), [{\pi \over 2},\pi), [\pi,{3\over 2}\pi), [{3\over 2}\pi,2\pi)\)。
而sin、cos在这些区间连续且单调,因此有唯一解。
举例,如果\(y'\)轴方向向量\(\bm{v}=(-1,0)\),那么\(x'\)轴方向向量\(\bm{u}\)应该在\(+y\)轴上(i.e. \(\bm{u}=(0,1)\)),且旋转矩阵为:
\[R=\begin{bmatrix}
u_x & u_y & 0\\
v_x & v_y & 0\\
0 & 0 & 1
\end{bmatrix}=\begin{bmatrix}
0 & 1 & 0\\
-1 & 0 & 0\\
0 & 0 & 1
\end{bmatrix}
\]
而根据(2),令\(θ={\pi\over 2}\),也能得到同样的旋转矩阵。
tips:这里只考虑旋转矩阵,没有考虑平移。如果要求平移矩阵,还需要知道\(x'y'\)系统原点在\(xy\)系统中的位置。
对于正交矩阵R,有
\[B[O';e_1',e_2',e_3']\xrightarrow{R}A[O;e_1,e_2,e_3]\iff P(x,y)^A\xrightarrow{R}P'(x',y')^B
\]
R的每个行向量,刚好是B系统的坐标轴单位向量。
三维坐标系变换
利用正交矩阵构筑旋转矩阵
类似于二维坐标系变换,三维空间下,也能用一组规范正交基构造旋转矩阵。
问题描述:将\(xyz\)系统(A)下的坐标描述转换到\(x'y'z'\)坐标系统(B)。
步骤:
1)T: 先将\(x'y'z'\)原点平移到\(xyz\)原点;
2)R: 进行一系列旋转使得对应坐标轴重合。如果2个坐标系比例不同,需要先缩放使比例相同。
如下图:
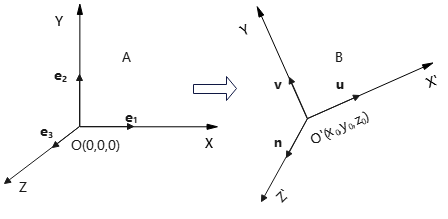
其中,\(\bm{u},\bm{v},\bm{n}\)分别为\(X', Y', Z'\)轴单位轴向量。B系统的原点\(O'\)在A系统的\((x_0,y_0,z_0)^A\)位置,坐标轴由\(xyz\)坐标轴旋转得到。
首先,将\(O'\)平移至\(O(0,0,0)^A\),对应平移矩阵\(T(-x_0,-y_0,-z_0)\)。
三维平移、旋转、缩放操作,参见计算机图形:三维几何变换。
\[\tag{8}
T(-x_0,-y_0,-z_0)=\begin{bmatrix}
1 & 0 & 0 & -x_0\\
0 & 1 & 0 & -y_0\\
0 & 0 & 1 & -z_0\\
0 & 0 & 0 & 1
\end{bmatrix}
\]
然后,用单位轴向量来构造坐标轴旋转矩阵,将单位轴向量\(\bm{u},\bm{v},\bm{n}\)分别转换到x、y、z轴上。构造方法类似于二维情形(参见(7))。
\[\tag{9}
R=\begin{bmatrix}
u_x & v_x & n_x & 0\\
u_y & v_y & n_y & 0\\
u_z & v_z & n_z & 0\\
0 & 0 & 0 & 1
\end{bmatrix}
\]
其中,B系统\(X',Y',Z'\)轴单位向量\(\bm{u}=(u_x,u_y,u_z)^A, \bm{v}=(v_x,v_y,v_z)^A, \bm{n}=(n_x,n_y,n_z)^A\)。
于是,复合变换矩阵:
\[\tag{10}
M_{xyz,x'y'z'}=R\cdot T(-x_0,-y_0,-z_0)
\]
A系统\(P\)点\(\to\)B系统\(P'\)点的变换:
\[P'=M_{xyz,x'y'z'}P
\]
变换矩阵的推导
上一节根据2D经验,构造出3D情形下坐标系变换对应的旋转矩阵,能否用数学方法推导出该变换呢?
答案是可以,不过要用到解析几何知识. (参见解析几何笔记:空间的正交变换和仿射变换).
笛卡尔坐标系下,平移、旋转、缩放都是空间的正交变换.
设正交变换\(ψ\),将直角标架\(Ⅰ[O;\bm{e_1},\bm{e_2},\bm{e_3}]\)变换为\(Ⅱ[O';\bm{e_1'},\bm{e_2'},\bm{e_3'}]\),其中\(O'(x_0,y_0,z_0)^Ⅰ\). 点的变换是直角标架的逆变换.
有\(Ⅰ[O;\bm{e_1},\bm{e_2},\bm{e_3}]\xrightarrow{ψ}Ⅱ[O';\bm{e_1'},\bm{e_2'},\bm{e_3'}]\)
∴
\[\begin{pmatrix}x'\\y'\\z'\end{pmatrix}
=A\begin{pmatrix}x\\y\\z\end{pmatrix}+\begin{pmatrix}x_0\\y_0\\z_0\end{pmatrix}
\]
将复合变换\(ψ\)分解为旋转变换\(σ\)和平移变换\(τ\)
\[ψ=τσ\\
σ:\begin{pmatrix}x'\\y'\\z'\end{pmatrix}=A_1\begin{pmatrix}x\\y\\z\end{pmatrix},
A_1=\begin{pmatrix}a_{11}&a_{12}&a_{13}\\
a_{21}&a_{22}&a_{23}\\
a_{31}&a_{32}&a_{33}\end{pmatrix}\\
τ:\begin{pmatrix}x'\\y'\\z'\end{pmatrix}=A_2\begin{pmatrix}x\\y\\z\end{pmatrix}+\begin{pmatrix}x_0\\y_0\\z_0\end{pmatrix},
A_2=I=\begin{pmatrix}1&&\\&1&\\&&1\end{pmatrix}
\]
∵\(Ⅰ[O;\bm{e_1},\bm{e_2},\bm{e_3}]\xrightarrow{ψ=τσ}Ⅱ[O';\bm{e_1'},\bm{e_2'},\bm{e_3'}]\)
∴
\[\begin{cases}
\overline{ψ}(\bm{e_1})=\bm{e_1'},\\
\overline{ψ}(\bm{e_2})=\bm{e_2'},\\
\overline{ψ}(\bm{e_3})=\bm{e_3'}
\end{cases}
\]
∵平移不改变向量大小、方向
∴对于任一向量\(\bm{α}\),\(\overline{ψ}(\bm{α})=\overline{τ}\overline{σ}(\bm{α})=\overline{τ}(\overline{σ}(\bm{α}))=\overline{σ}(\bm{α})\)
∴
\[\begin{cases}
\overline{ψ}(\bm{e_1})=\overline{σ}(\bm{e_1})=\bm{e_1'},\\
\overline{ψ}(\bm{e_2})=\overline{σ}(\bm{e_1})=\bm{e_2'},\\
\overline{ψ}(\bm{e_3})=\overline{σ}(\bm{e_1})=\bm{e_3'}
\end{cases}
\]
∵已知
\[\bm{e_1}=\begin{pmatrix}1\\0\\0\end{pmatrix},
\bm{e_2}=\begin{pmatrix}0\\1\\0\end{pmatrix},
\bm{e_3}=\begin{pmatrix}0\\0\\1\end{pmatrix}\\
\bm{e_1'}=\bm{u}=\begin{pmatrix}u_x\\u_y\\u_z\end{pmatrix},
\bm{e_2'}=\bm{v}=\begin{pmatrix}v_x\\v_y\\v_z\end{pmatrix},
\bm{e_3'}=\bm{n}=\begin{pmatrix}n_x\\n_y\\n_z\end{pmatrix}
\]
对于\(\bm{e_1}\to \bm{e_1'}\),
\[\begin{aligned}
\begin{pmatrix}u_x\\u_y\\u_z\end{pmatrix} &= A_2\begin{pmatrix}1\\0\\0\end{pmatrix}\\
\implies
u_x &= a_{11}\\
u_y &= a_{21}\\
u_z &= a_{31}
\end{aligned}
\]
同理,可由\(\bm{e_2}\to \bm{e_2'}, \bm{e_3}\to \bm{e_3'}\)分别得出:
\[v_x=a_{21},v_y=a_{22},v_z=a_{23}\\
n_x=a_{31},n_y=a_{32},n_z=a_{33}
\]
∴\(A_2=\begin{pmatrix}a_{11}&a_{12}&a_{13}\\
a_{21}&a_{22}&a_{23}\\
a_{31}&a_{32}&a_{33}\end{pmatrix}
=\begin{pmatrix}u_x&v_x&n_x\\
u_y&v_y&n_y\\
u_z&v_z&n_z\end{pmatrix}\)
于是,
\[ψ:\begin{pmatrix}x'\\y'\\z'\end{pmatrix}
=\begin{pmatrix}u_x&v_x&n_x\\
u_y&v_y&n_y\\
u_z&v_z&n_z\end{pmatrix}
\begin{pmatrix}x\\y\\z\end{pmatrix}+\begin{pmatrix}x_0\\y_0\\z_0\end{pmatrix}
\]
写成齐次坐标形式:
\[ψ:\begin{pmatrix}x'\\y'\\z'\\1\end{pmatrix}
=\begin{pmatrix}u_x&v_x&n_x&x_0\\
u_y&v_y&n_y&y_0\\
u_z&v_z&n_z&z_0\\
0&0&0&1\end{pmatrix}
\begin{pmatrix}x\\y\\z\\1\end{pmatrix}
\]
已经求出直角标架的变换,而我们要求的是点的变换,如何求?
∵点的变换是直角标架的逆变换
∴点的变换
\[\begin{pmatrix}x\\y\\z\end{pmatrix}=A^{-1}\begin{pmatrix}x'\\y'\\z'\end{pmatrix}-A^{-1}\begin{pmatrix}x_0\\y_0\\z_0\end{pmatrix}
\]
∵直角标架的旋转、平移变换是正交变换
∴复合变换也是正交变换
∴\(A\)是正交矩阵
∴\(A^{-1}=A^T=\begin{pmatrix}u_x&u_y&u_z\\
v_x&v_y&v_z\\
n_x&n_y&n_z\end{pmatrix}\)
注意:只有正交变换对应的过渡矩阵才是正交矩阵,齐次变换的系数矩阵不一定是正交矩阵.(过渡矩阵参见解析几何笔记:平面的正交变换)
∴
\[\begin{aligned}
\begin{pmatrix}x\\y\\z\end{pmatrix}
&= A^T\begin{pmatrix}x'\\y'\\z'\end{pmatrix}-\begin{pmatrix}u_x&u_y&u_z\\
v_x&v_y&v_z\\
n_x&n_y&n_z\end{pmatrix}\begin{pmatrix}x_0\\y_0\\z_0\end{pmatrix}\\
&= A^T\begin{pmatrix}x'\\y'\\z'\end{pmatrix}-\begin{pmatrix}u_xx_0 + u_yy_0 + u_zz_0\\
v_xx_0 + v_yy_0 + v_zz_0\\
n_xx_0 + n_yy_0 + n_zz_0\end{pmatrix}\\
&= A^T\begin{pmatrix}x'\\y'\\z'\end{pmatrix}-\begin{pmatrix}\bm{u}\cdot\bm{O'}\\ \bm{v}\cdot \bm{O'}\\ \bm{n}\cdot \bm{O'} \end{pmatrix}
\end{aligned}
\]
写成齐次坐标形式:
\[\begin{pmatrix}x\\y\\z\\1\end{pmatrix}=
\begin{pmatrix}u_x&u_y&u_z&-\bm{u}\cdot\bm{O'}\\
v_x&v_y&v_z&-\bm{v}\cdot \bm{O'}\\
n_x&n_y&n_z&-\bm{n}\cdot \bm{O'}\\
0&0&0&1\end{pmatrix}\begin{pmatrix}x'\\y'\\z'\\1\end{pmatrix}
\]
这就是点\(P(x,y,z)\)从\(A\)系统变换到B系统的变换矩阵:
\[M_{xyz,x'y'z'}=\begin{pmatrix}u_x&u_y&u_z&-\bm{u}\cdot\bm{O'}\\
v_x&v_y&v_z&-\bm{v}\cdot \bm{O'}\\
n_x&n_y&n_z&-\bm{n}\cdot \bm{O'}\\
0&0&0&1\end{pmatrix}
\]
小结
坐标系的转换与对象的转换是反的. i.g. \(x'y'\)轴转换到\(xy\)轴,但该变换对应:将\(xy\)系统的对象转换到\(x'y'\)系统。







 浙公网安备 33010602011771号
浙公网安备 33010602011771号