tinyrenderer笔记：透视投影

目录

• 从2D到3D
• 透视投影模型
• 比较不同的透视投影模型
• 参考

从2D到3D

2D点放到平面\(z=1\)，得3D点\((\frac{x}{z}, \frac{y}{z},1)\).

如果将3D点投影到2D平面呢？
观察坐标系下，在原点和要投影的点\(P\)之间，画一条直线，然后找到它与平面\(z=1\)的交点\(P'\)，即为\(P\)在平面\(z=1\)上的投影点.

2D平面（品红色），3D点\((x,y,z)\)投影得到2D点\((\frac{x}{z},\frac{y}{z})\)：

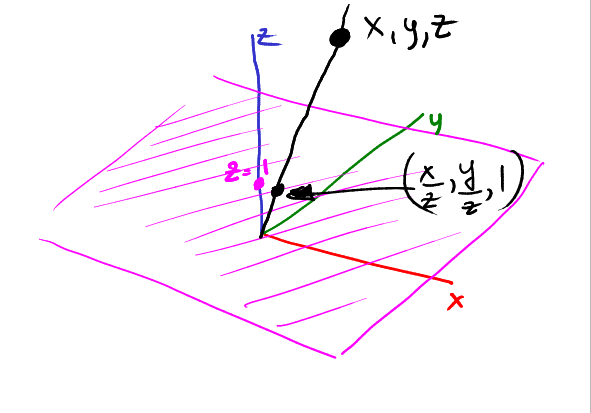
如果过\((x,y,1)\)作一条直线\(//z\)轴，\((x,y,1)\)将投影到哪里？\((x,y)\)：

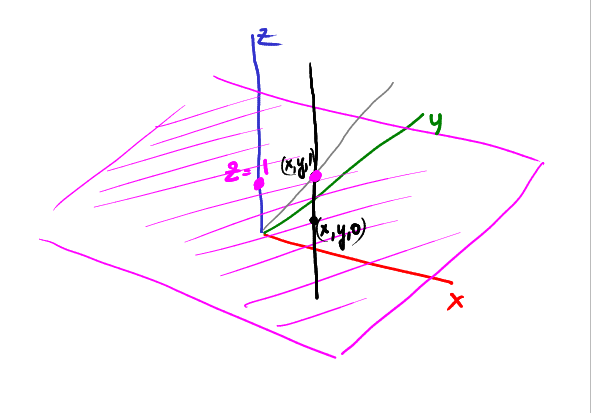
如果过点\((x,y,\frac{1}{2})\)呢？将投影到\((2x,2y)\)：

说明：我们最终要投影到的平面是\(z=1\). 对于\((x,y,\frac{1}{2})\)，连接其与原点，与平面\(z=1\)的交点，就是投影点\((2x,2y,1)\).

如果过点\((x,y,\frac{1}{4})\)呢？将投影到\((4x,4y)\)：

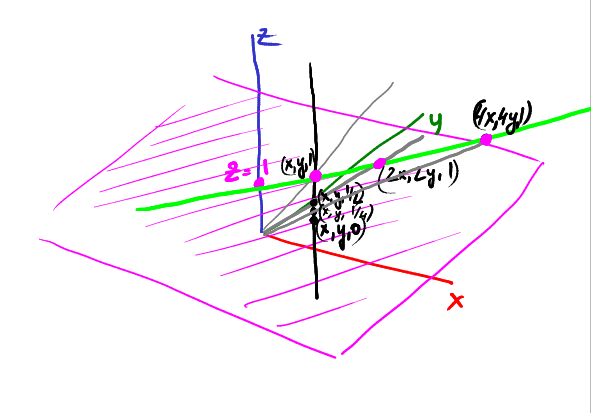
如果继续该过程，接近\(z=0\)，那么投影点将远离原点，即\((x,y,0)\)被投影到\((x,y)\)方向上的无穷远处. 此时，\((x,y)\)代表方向，而非投影点.

为什么使用齐次坐标？

齐次坐标允许区分向量和点. 3D空间下，很难区分\((x,y)\)是点，还是方向；但如果使用齐次坐标，所有\(z=0\)的东西都是向量，其余都是点. 例如，\((x,y,0)\)代表\((x,y)\)方向，\((x,y,1)\)代表投影点\((x,y,1)\)，\((x,y,2)\)代表投影点\((2x,2y,1)\).

并且遵循计算特性：向量 + 向量 = 向量，点 + 向量 = 点，矢量 - 矢量 = 矢量.

透视投影模型

3D点\((x,y,z)\)用1增广得到4D点\((x,y,z,1)\). 如何逆投影回3D？
例如，做如下仿射变换：

\[\begin{pmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & r & 1 \end{pmatrix} \begin{pmatrix} x\\y\\z\\1 \end{pmatrix} =\begin{pmatrix} x\\y\\z\\rz+1 \end{pmatrix} \]

从4D点到3D投影点对应关系：

\[\begin{pmatrix} x\\y\\z\\rz+1 \end{pmatrix}\to \begin{pmatrix} \frac{x}{rz+1}\\\frac{y}{rz+1}\\\frac{z}{rz+1} \end{pmatrix} \]

注：4D点投影到\(w=rz+1\)，需要\((x/w,y/w,z/w)\),变成3D点.

3D空间下，在中心投影模型（相机观察模型）中，相机位于z轴\((0,0,c)\)，给定点\(P=(x,y,z)\)，我们想将P点投影到2D平面\(z=0\)，需要求出\(P\to P'\)的变换.

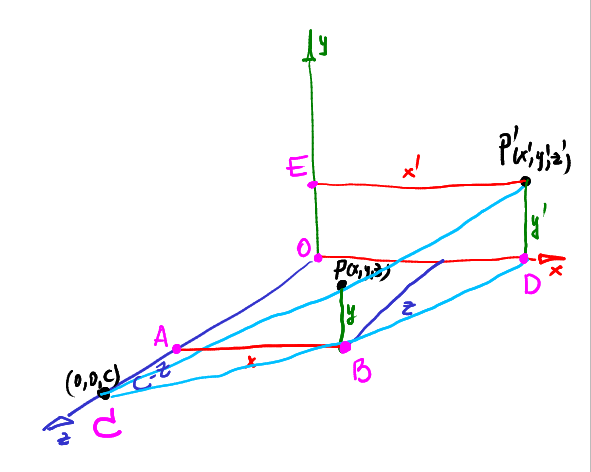
对于\(x\to x'\)，

\[\because △ABC\sim △ODC\\ \therefore \frac{|AB|}{|AC|}=\frac{|OD|}{|OC|}\\ \therefore \frac{x}{c-z} = \frac{x'}{c}\\ \therefore x'=\frac{x}{1-\frac{z}{c}} \]

同理（也可由x、y的对称性），对于\(y\to y'\)，有

\[y'=\frac{y}{1-\frac{z}{c}} \]

∴可得前面仿射变换\(r=-\frac{1}{c}\)

于是，从\(P(x,y,z)\to P'(x',y',z')\)的变换：

\[\begin{pmatrix} x\\y\\z \end{pmatrix} \xrightarrow{expand} \begin{pmatrix} x\\y\\z\\1 \end{pmatrix}\\ \begin{pmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & -\frac{1}{c}& 1 \end{pmatrix} \begin{pmatrix} x\\y\\z\\1 \end{pmatrix} =\begin{pmatrix} x\\y\\z\\1-\frac{z}{c} \end{pmatrix}\\ \begin{pmatrix} x\\y\\z\\1-\frac{z}{c} \end{pmatrix} \xrightarrow{projection}\begin{pmatrix} \frac{x}{1-\frac{z}{c}}\\\frac{y}{1-\frac{z}{c}}\\\frac{z}{1-\frac{z}{c}} \end{pmatrix} \]

对于投影点\(P'\)在\(CP\)之间的情形，该变换也成立.

比较不同的透视投影模型

之前，我们也有个透视投影模型，对应了一个透视投影变换矩阵，简单描述见计算机图形：mvp变换（模型、视图、投影变换），详细推导见计算机图形：三维观察之投影变换
.

都是透视投影变换，它们有什么区别呢？

为方便描述，之前的模型，简称模型A，这里的模型简称B. 透视投影变换，一定是基于我们的观察模型的.

模型A：

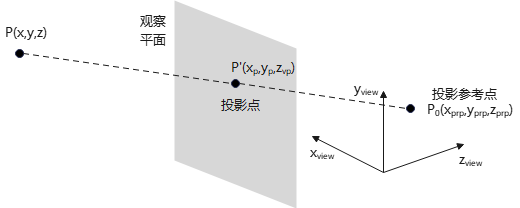
模型B：

不同点：

1）投影参考点

模型A，投影参考点位于观察原点\((0,0,0)\)，并与相机位置重合；
模型B，投影参考点位于相机\((0,0,c)\)；

2）投影平面

模型A，投影到近平面\(z=n\)；
模型B，投影到平面\(z=0\)；

参考

Lesson-4:-Perspective-projection