计算机图形：三角形及重心空间

目录

• 三角形
  • 2D三角形
  • 重心空间
    • 点到直线的距离
    • 重心坐标插值
    • 计算重心坐标
      • 方法一：用三角形顶点坐标表示
      • 方法二：用三角形面积表示
      • 方法三：用叉积表示
• 参考

三角形

三角形是图形程序的基本建模单元. 诸如颜色之类信息，通常被标记到三角形顶点上，需要通过该三角形插值. 插值过程在称为重心坐标系（barycenric coordinates）的坐标系统上进行.

2D三角形

2D空间下，默认直角标架\(Ⅰ[O;\bm{e_1},\bm{e_2}]\). 点a,b,c是三角形3顶点，坐标分别为\((x_a,y_a)_Ⅰ,(x_b,y_b)_Ⅰ,(x_c,y_c)_Ⅰ,\)，那么三角形的有向面积：

\[\tag{1} \begin{aligned} S&=\frac{1}{2}\overrightarrow{ab}\times \overrightarrow{ac}\\ &=\frac{1}{2}(x_b-x_a,y_b-y_a)\times (x_c-x_a,y_c-y_a)\\ &=\frac{1}{2}(a_1,a_2)\times (b_1,b_2)\\ &=\frac{1}{2}(a_1e_1+a_2e_2)\times (b_1e_1+b_2e_2)\\ &=\frac{1}{2}(a_1b_1-a_2b_1)e_3,(e_3=e_1e_2)\\ &=\frac{1}{2}\begin{vmatrix}a_1&b_1\\a_2&b_2\end{vmatrix}\\ &=\frac{1}{2}\begin{vmatrix} x_b-x_a & x_c-x_a\\ y_b-y_a & y_c-y_a \end{vmatrix}\\ &=\frac{1}{2}(x_ay_b+x_by_c+x_cy_a-x_ay_c-x_by_a-x_cy_b) \end{aligned} \]

当a,b,c逆时针顺序时，S方向为正；否则，S方向为负.

重心空间

点到直线的距离

这部分作为引理，为后续推导重心插值公式.

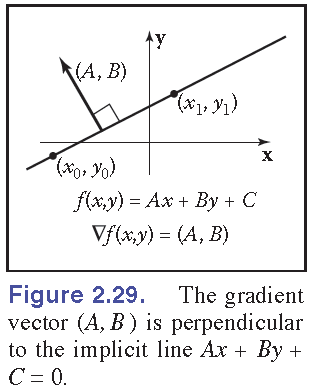
以直线\(L:f(x,y)=Ax+By+C=0\)梯度方向作向量\((A,B)\)，那么\((A,B)⊥L\).

证明：

∵直线L经过\((x_0,y_0),(x_1,y_1)\)

∴

\[\begin{cases} Ax_0+By_0+C=0 & ①\\ Ax_1+By_1+C=0 & ② \end{cases}\\ \]

∴\(②-① = A(x_1-x_0) + B(y_1-y_0) = 0\)

∵\((x_1-x_0, y_1-y_0)\cdot (A, B)=A(x_1-x_0) + B(y_1-y_0)=0\)

∴\((A, B)⊥(x_1-x_0,y_1-y_0)\)

而\((x_1-x_0,y_1-y_0)//L\)

∴\((A,B)⊥L\)

---

tips: 直线\(L:f(x,y)=Ax+By+C\)梯度方向为什么是\((A,B)\)？

证明：
设\(P_0(x_0,y_0)\)是\(f(x,y)\)上一点，那么，

\[\begin{aligned} \bm{grad}f(x_0,y_0) &=f_x(x_0,y_0)\bm{i}+f_y(x_0,y_0)\bm{j}\\ &=A\bm{i}+B\bm{j}\\ &=(A,B) \end{aligned} \]

---

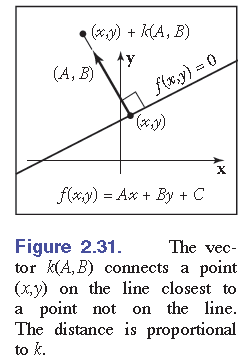
引理 任一点\(P(a,b)\)到直线\(f(x,y):Ax+By+C=0\)的距离

\[d_p=\frac{f(a,b)}{\sqrt{A^2+B^2}} \]

证明：
在直线L上任取一点\(P_0=(x,y)\)，从该点沿着向量\((A,B)\)方向确定另一点\(P=(x,y)+k(A,B), k\in R\)

那么，求点\(P\)到直线L的距离，可转化为求\(|P_0P|\).

\[|P_0P|=|k(A,B)|=k\sqrt{A^2+B^2}, k\in R \]

其中，k为常数，代表沿着\((A,B)\)的方向（同向 or 反向）.

现已知P点坐标\((a,b)\)，如何求P到L距离？或者说，如何确定k值？

\[P=(a,b)\implies P_0=(a,b)-k(A,B)=(a-kA,b-kB) \]

∵\(P_0\)在直线L上
∴\(f(a-kA,b-kB)=A(a-kA)+B(b-kB)+C=0\)
∴

\[k=\frac{Aa+Bb+C}{A^2+B^2}=\frac{f(a,b)}{A^2+B^2} \]

∴点\(P(a,b)\)到直线\(f(x,y):Ax+By+C=0\)的距离：

\[d_p=|P_0P|=\frac{f(a,b)}{\sqrt{A^2+B^2}} \]

重心坐标插值

有时，我们希望为三角形顶点赋予属性，如颜色，并在三角形上平滑插值. 用重心坐标（barycentric coordinates）是最简单的办法.

重心坐标系是仿射坐标系，而非正交坐标系. 仿射坐标系参见解析几何笔记：仿射坐标系.

对于\(△ABC\)内任一点\(P\)，其坐标满足重心坐标公式：

\[\bm{P}=α\bm{A}+β\bm{B}+γ\bm{C},α+β+γ=1,α,β,γ\in [0, 1] \]

下面求重心坐标\(α,β,γ\).

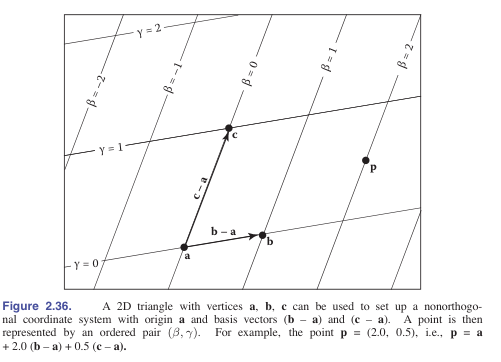
如上图，以\(△abc\)的\(a\)点为原点、两边\(\overrightarrow{ab},\overrightarrow{ac}\)为基向量（不平行），建立仿射标架\(Ⅱ[a;\overrightarrow{ab},\overrightarrow{ac}]\)，任一点p在\(Ⅰ\)中坐标：\((x_p,y_p)_Ⅰ\)，在\(Ⅱ\)中坐标\((β,γ)_Ⅱ\).

有

\[\tag{2} \begin{aligned} \bm{p-a}&=β(\bm{b}-\bm{a})+γ(\bm{c}-\bm{a})\\ \bm{p}&=\bm{a}+β(\bm{b}-\bm{a})+γ(\bm{c}-\bm{a})\\ \bm{p}&=(1-β-γ)\bm{a}+β\bm{b}+γ\bm{c} \end{aligned} \]

令\(α=1-β-γ\)，则

\[\tag{3} \bm{p}(α,β,γ)=α\bm{a}+β\bm{b}+γ\bm{c},α+β+γ=1 \]

这样，p点坐标用三角形顶点a,b,c表示. 式(3)就是重心坐标插值公式.

p点与\(△abc\)关系：

• p在\(△abc\)内部，当且仅当\(α,β,γ\in (0,1)\)；
• 如果\(α,β,γ\)中有1项为0，另2项\(\in (0,1)\)，则p在三角形边界时；
• 如果有2项为0，另1项为1，则p在三角形顶点；
• \(α,β,γ\)中至少有1项\(<0\)，则至少有1项\(>1\)，此时p在三角形外部（但还在三角形平面上）.

式(3)不仅用于坐标混合，也可用于其他属性混合.

将式(2)写成坐标形式：

\[\tag{4} \begin{aligned} \bm{p-a}&=β(\bm{b}-\bm{a})+γ(\bm{c}-\bm{a})\\ \begin{pmatrix}x_p-x_a\\y_p-y_a \end{pmatrix}&=\begin{pmatrix}x_b-x_a&x_c-x_a\\y_b-y_a&y_c-y_a\end{pmatrix} \begin{pmatrix}β\\ γ\end{pmatrix} \end{aligned} \]

计算重心坐标

方法一：用三角形顶点坐标表示

∵\(α=1-β-γ\)
∴求出\(β,γ\)即可.

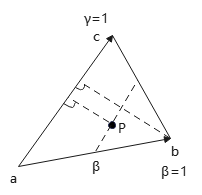
由三角形相似性，P到直线ac距离\(d_{ac,p}\)与P在Ⅱ下坐标满足：

\[\frac{β}{1}=\frac{d_{ac,p}}{d_{ac,b}} \]

而平面上任一点\(P(x_p,y_p)\)到直线\(ac:f_{ac}(x,y)=Ax+By+C=0\)距离：

\[d_{ac,p}=\frac{f_{ac}(x_p,y_p)}{\sqrt{A^2+B^2}} \]

因此，

\[β=\frac{d_{ac,p}}{d_{ac,b}}=\frac{f_{ac}(x_p,y_p)}{f_{ac}(x_b,y_b)} =\frac{Ax_p+By_p+C}{Ax_b+By_b+C} \]

问题转化为求A、B、C，即求直线ac方程.

∵\(f_{ac}(x,y)=0\)过a,c点

∴

\[\begin{cases} Ax_a+By_a+C=0\\ Ax_c+By_c+C=0 \end{cases} \]

∴

\[A(x_c-x_a)+B(y_c-y_a)=0 \]

∴向量\((A,B)⊥(x_c-x_a,y_c-y_a)\)
不妨取\((A,B)=(y_a-y_c,x_c-x_a)\). 又直线ac过点\(a(x_a,y_a)\)，可得

\[\begin{aligned} f_{ac}(x_a,y_a)&=Ax_a+By_a+C\\ &=(y_a-y_c)x_a+(x_c-x_a)y_a+C=0\\ \implies C &=(y_c-y_a)x_a+(x_a-x_c)y_a=x_ay_c-x_cy_a \end{aligned} \]

因此，直线ac方程：

\[(y_a-y_c)x+(x_c-x_a)y+x_ay_c-x_cy_a=0 \]

∴

\[β=\frac{(y_a-y_c)x_p+(x_c-x_a)y_p+x_ay_c-x_cy_a}{(y_a-y_c)x_b+(x_c-x_a)y_b+x_ay_c-x_cy_a} \]

同理，

\[\begin{aligned} γ&=\frac{d_{ab,p}}{d_{ab,c}}\\ &=\frac{f_{ab}(x_p,y_p)}{f_{ab}(x_c,y_c)}\\ &=...\\ &=\frac{(y_a-y_b)x_p+(x_b-x_a)y_p+x_ay_b-x_by_a}{(y_a-y_b)x_c+(x_b-x_a)y_c+x_ay_b-x_by_a}\\ α&=1-β-γ \end{aligned} \]

注意：b、P都不在直线ac上.

方法二：用三角形面积表示

重心插值参数\(α,β,γ\)，还能用面积计算：

\[α=\frac{A_c}{A},β=\frac{A_b}{A},γ=\frac{A_a}{A} \]

其中，\(A,A_a,A_b,A_c\)分别表示\(△abc,△Pbc,△Pca,△Pab\)的有向面积.

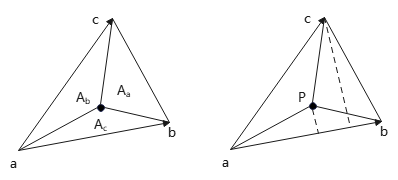
\(P、c\)到直线\(ab\)距离，可看作\(△abP、△abc\)的高，底边都是ab，那么

\[γ=\frac{d_{ab,p}}{d_{ab,c}}=\frac{A_c}{A} \]

这里，\(A,A_a,A_b,A_c\)分别表示\(△abc,△Pbc,△Pca,△Pab\)的面积.（注意顶点逆时针顺序）

同理，

\[\begin{aligned} α=\frac{A_a}{A}\\ β=\frac{A_b}{A} \end{aligned} \]

然后，可根据前面三角形有向面积公式，计算三角形面积，从而将\(α,β,γ\)转化为\(a,b,c\)坐标表示：

\[\begin{aligned} A &= \frac{1}{2}\overrightarrow{ab}\times \overrightarrow{ac}=\frac{1}{2}(x_ay_b + x_by_c + x_cy_a - x_ay_c - x_by_a - x_cy_b)\\ A_a &= \frac{1}{2}\overrightarrow{pb}\times \overrightarrow{pc}=\frac{1}{2}(x_py_b + x_by_c + x_cy_p - x_py_c - x_by_p - x_cy_b)\\ A_b &= \frac{1}{2}\overrightarrow{pa}\times \overrightarrow{pc}=\frac{1}{2}(x_ay_p + x_py_c + x_cy_a - x_ay_c - x_py_a - x_cy_p)\\ A_c &= \frac{1}{2}\overrightarrow{pa}\times \overrightarrow{pb}=\frac{1}{2}(x_ay_b + x_by_p + x_py_a - x_ay_p - x_by_a - x_py_b) \end{aligned} \]

方法三：用叉积表示

先说结论：重心坐标还可以表示成

\[\bm{P}=(1-\frac{a}{c}-\frac{b}{c})\bm{A}+\frac{a}{c}\bm{B}+\frac{b}{c}\bm{C}, c\neq 0 \]

其中，\((a,b,c)=(u_x,u_y,u_z)=\overrightarrow{u}=(B_x-A_x, C_x-A_x, A_x-P)\times (B_y-A_y,C_y-A_y,A_y-P)\).

这是开源项目tinyrender Lesson-2常用的一种表示方法.

推导：
∵\(\bm{P}=α\bm{A}+β\bm{B}+γ\bm{C},α+β+γ=1,α,β,γ\in [0, 1]\)

∴\(\bm{P}=(1-β-γ)\bm{A}+β\bm{B}+γ\bm{C}\)

∴\(\bm{P}=\bm{A}+β(\bm{B}-\bm{A})+γ(\bm{C}-\bm{A})\)

∴\(β\overrightarrow{AB}+γ\overrightarrow{AC}+\overrightarrow{PA}=0\)

∵\(A,B,C,P\)是在同一\(xy\)平面
∴按\(x,y\)维度拆开方程组，得：

\[\begin{cases} β\overrightarrow{AB}_x+γ\overrightarrow{AC}_x+\overrightarrow{PA}_x=0\\ β\overrightarrow{AB}_y+γ\overrightarrow{AC}_y+\overrightarrow{PA}_y=0 \end{cases} \]

∴向量\((β,γ,1) ⊥ \overrightarrow{s_1}=(\overrightarrow{AB}_x,\overrightarrow{AC}_x,\overrightarrow{PA}_x), \overrightarrow{s_2}=(\overrightarrow{AB}_y,\overrightarrow{AC}_y,\overrightarrow{PA}_y)\).

于是，

\[(β,γ,1) = \overrightarrow{s_1}\times \overrightarrow{s_2}, α=1-β-γ \]

其中，\(\overrightarrow{s_1}=(B_x-A_x, C_x-A_x, A_x-P), \overrightarrow{s_2}=(B_y-A_y,C_y-A_y,A_y-P)\)

记\(\overrightarrow{u}=\overrightarrow{s_1}\times \overrightarrow{s_2}=(u_x,u_y,u_z)=(a,b,c)//(β,γ,1)\)

∴存在λ使得

\[\begin{aligned} &\begin{cases} a=λβ\\ b=λγ,&λ\neq 0\\ c=λ \end{cases}\\ \implies &\begin{cases} β=\frac{a}{c}\\ γ=\frac{b}{c},&c\neq 0\\ α=1-β-γ=1-\frac{a}{c}-\frac{b}{c} \end{cases} \end{aligned} \]

∴

\[\bm{P}=α\bm{A}+β\bm{B}+γ\bm{C}=(1-\frac{a}{c}-\frac{b}{c})\bm{A}+\frac{a}{c}\bm{B}+\frac{b}{c}\bm{C},c\neq 0 \]

而

\[(a,b,c)=(u_x,u_y,u_z)=\overrightarrow{s_1}\times \overrightarrow{s_2}=(B_x-A_x, C_x-A_x, A_x-P)\times (B_y-A_y,C_y-A_y,A_y-P) \]

注意：这里\(a,b,c\)是\(\overrightarrow{u}\)的坐标分量，不是三角形顶点.

思考：\(c\)是否能为0？

假设\(c=0\)，则\(a\overrightarrow{AB}+b\overrightarrow{AC}=0\)

那么\(\overrightarrow{AB}//\overrightarrow{AC}\)，即\(A,B,C\) 3点共线，不构成三角形. 与已知条件矛盾

∴\(c\neq 0\)

思考：\(\bm{P}\)与\(△ABC\)关系如何？

可以参考前面的\(\bm{P}=α\bm{A}+β\bm{B}+γ\bm{C}, α=1-\frac{a}{c}-\frac{b}{c},β=\frac{a}{c},γ=\frac{b}{c}\)

只考虑\(c>0\)情形，\(c<0\)情形类似：

• \(P\)在\(△ABC\)内部：\(α,β,γ\in (0, 1)\iff a,b>0, a+b<c\)；
• \(P\)在\(△ABC\)边上：\(α,β,γ\)中1项为0，另外2项 \(\in (0,1) \iff \begin{cases}a=0, 0<b<c \\ b=0, 0<a<c \\ a+b=c, a,b>0 \end{cases}\)（满足一条即可）；
• \(P\)在\(△ABC\)顶点：\(α,β,γ\)中2项为0，另1项 \(\in (0, 1)\iff \begin{cases}a=b=0\\ a=0,b=c\\ b=0,a=c\end{cases}\)（满足一条即可）；
• \(P\)在\(△ABC\)外部：\(α,β,γ\)中至少1项\(<0 \iff \begin{cases}a<0\\b<0\\a+b>c\end{cases}\)（满足一条即可）

参考

[1] Shirley P .Fundamentals of Computer Graphics[M]. 2015.

[2] tinyrender 03_填充三角形

[3] Barycentric