函数极限定义、性质与四则运算

向对本文提出改进意见的 ytez 致谢！

我们正式地说一下 函数极限。

\[\lim_{x\to x_0}f(x) = A \]

这句话表示 \(f(x)\) 在 \(x_0\) 的极限为 \(A\)（收敛于 \(A\)）。
也即：当自变量趋于 \(x_0\) 时，因变量趋于 \(A\)。

🔋铺垫——本文所用到的没在文章中详细说明的特殊符号

注意，每个人的文章所用的符号的含义可能有细微差异，这并不要紧。
这恰恰体现了数学的自由之美。

符号	含义	举例
\(+\infty\)	正无穷大	这个显然并不用举例，对吧
\(-\infty\)	负无穷大	同上
\(\infty\)	无穷大（正和负的统称）	\(f(x) = \dfrac{1}{x}\) 在 \(x = 0\) 为 \(\infty\)（虽然不太严谨）
\(\mathbb{R}\)	全体实数构成的集合	\(1,0.333\dots,\pi\) 都属于这个集合
\(\forall\)	对于任意	\(\forall x < 0\) 表示对于任意满足 \(x < 0\) 的 \(x\)；\(\forall x(0 < x < 1)\) 表示对于任意满足 \(0 < x < 1\) 的 \(x\)
\(\exists\)	存在	\(\exists x < 0\) 表示存在一个（当然可以有好多个）满足 \(x < 0\) 的 \(x\)；\(\exists x(0 < x < 1)\) 表示存在一个（也可以有好多个）满足 \(0 < x < 1\) 的 \(x\)
\(\forall\dots\) : \(\dots\)	对于任意满足 \(\dots\) 条件的，有 \(\dots\)（或者说是满足 \(\dots\) 的条件）	\(\forall x > 0 : \dfrac{1}{x} > 0\) 表示对于任意满足条件的 \(x\)，有 \(\dfrac{1}{x} > 0\)（满足 \(\dfrac{1}{x} > 0\)）
\(|x| < a\)	\(-a < x < a\)	（只是想单独说明一下；还有就是 \(a\) 当然不能小于等于 \(0\)！）
\(\min\{a_1, a_2,\dots, a_n\}\)	\(a_1,a_2,\dots,a_n\) 中的最小值	\(\min\{1, 2, 3\} = 1\)
\(\max\{a_1, a_2,\dots, a_n\}\)	\(a_1,a_2,\dots,a_n\) 中的最大值	\(\max\{1, 2, 3\} = 3\)

✏️定义

这里分为几种情况。
我们把上面这个式子 \(break\) 成两个部分。

🥇\(Part\) \(1\)

即 \(\displaystyle \lim_{x\to x_0}\) 。
我们对 \(x_0\) 分 \(4\) 种情况，即有限、\(\infty\)、\(+\infty\)、\(-\infty\)。
他们对应的描述语言分别为

\[\exists \delta > 0, \forall x(0 < |x - x_0| < \delta) \]

\[\exists \delta > 0, \forall x(|x| > \delta) \]

\[\exists \delta > 0, \forall x > \delta \]

\[\exists \delta > 0, \forall x < -\delta \]

🥈\(Part\) \(2\)

即 \(f(x) = A\)。
我们仍分 \(4\) 种情况，同上。
他们对应的描述语言分别为

\[\forall \varepsilon > 0, Part\ 1:|f(x) - A| < \varepsilon \]

\[\forall \varepsilon > 0, Part\ 1:|f(x)| > \varepsilon \]

\[\forall \varepsilon > 0, Part\ 1:f(x) > \varepsilon \]

\[\forall \varepsilon > 0, Part\ 1:f(x) < -\varepsilon \]

其中这个 \(Part\ 1\) 是指把 \(Part\ 1\) 中的描述语言插入进去（看下面）。

🏆\(Make\ them\ together.\)

比如说我们想要表达

\[\lim_{x\to x_0}f(x) = A \]

其中 \(x_0,A\) 都是有限的数（以后就不做特殊说明了）。
我们直接从 \(Part\ 1\) 中抽取

\[\exists \delta > 0, \forall x(0 < |x - x_0| < \delta) \]

并从 \(Part\ 2\) 中抽取

\[\forall \varepsilon > 0, Part\ 1:|f(x) - A| < \varepsilon \]

把它们 \(mix\ up\)，得到

\[\forall \varepsilon > 0, \exists \delta > 0, \forall x(0 < |x - x_0| < \delta) : |f(x) - A| < \varepsilon \]

这么长的一句话让我们感到十分无力
所以也可以用文字表示：

\[对于任意\ \varepsilon > 0，存在\ \delta > 0，使得对于任意满足\ 0 < |x - x_0| < \delta\ 的\ x，有\ f(x) - A < \varepsilon \]

好吧，这样更长了（晕）

🤔我们为什么这么定义

想一想，什么是极限？
当自变量趋于一个数时，因变量趋于一个数。

我们为什么一定要是 趋于 呢，为什么不是直接取那个位置的数？
因为我们的函数有可能是分段的，或是在一个点没有定义。
所以我们的极限指的是那个位置的数 应该是什么。
\(For\ Example\)，我们考虑 \(x_0, A\) 都有限的情况，且函数 \(f(x)\) 在 \(x_0\) 没有定义。

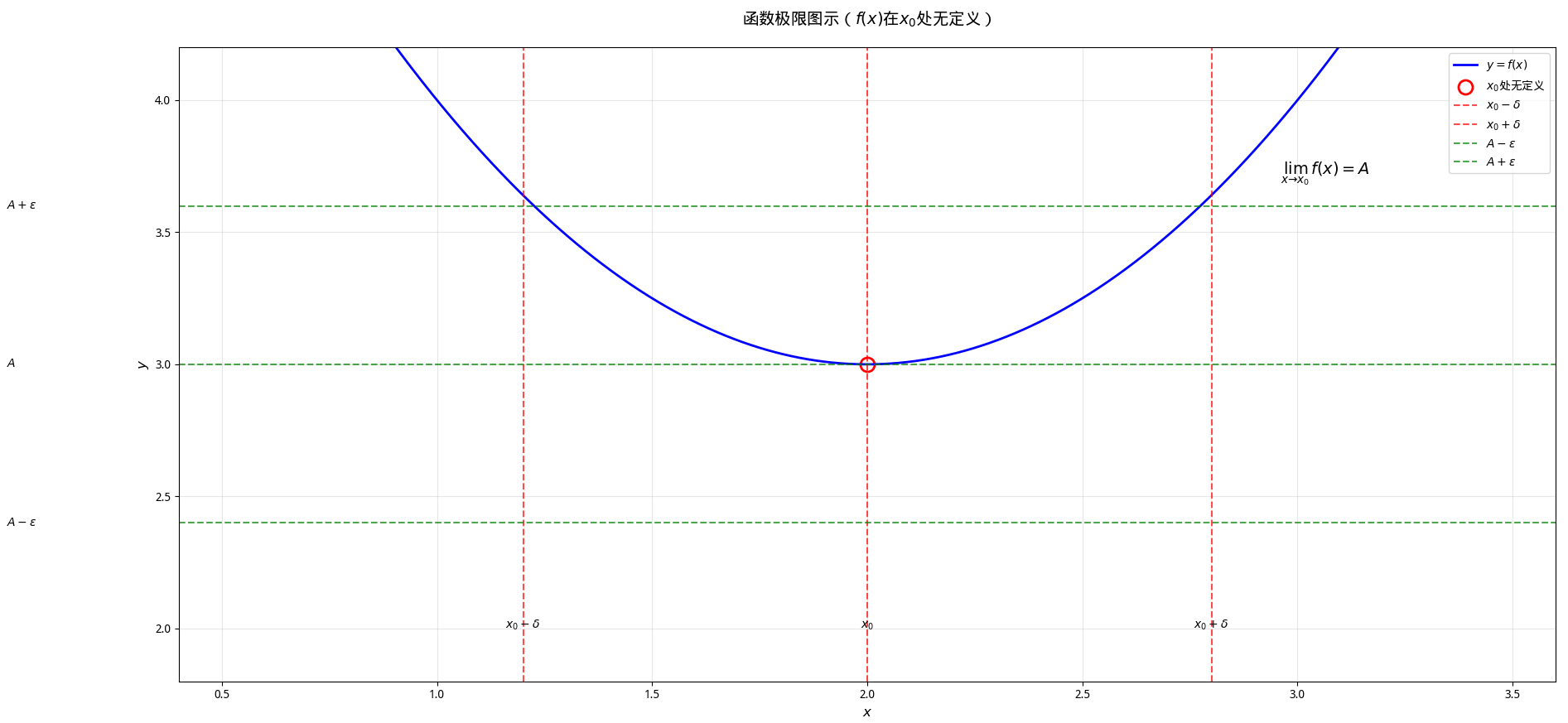
（我用AI画的有点唐，凑合看吧 ToT）

当 \(A + \varepsilon\) 和 \(A - \varepsilon\) 越来越接近 \(A\) 的时候，\(x - \delta\) 和 \(x + \delta\) 也越来越接近 \(x_0\)。
那就意味着当它们无限接近于 \(A,x_0\) 的时候，我们就可以说这个位置的极限就是 \(A\) 了。
反过来看，如果我们要验证一个函数的极限是不是 \(A\)，那我们只需要看一下当 \(\varepsilon\) 越来越小的时候，是不是存在 \(\delta\)，使得在左右两条红线范围里的函数值都在上下两条绿线的范围里就行，因为这时对于任意 \(x\not= x_0\)，有 \(f(x)\) 无限接近 \(A\)。（好好想一想）

😜似乎不怎么重要的单侧极限

👉左极限

\[\displaystyle\lim_{x\to x_0-}f(x) = A \]

为什么这个手指是向右的呢？
因为左极限的“左”并不是向左边，而是 从左向右。
也就是说，左极限是在 \((x_0 - \delta, x_0)\) 这个范围里的。
因此，我们只需要把 \(Part\ 1\) 的语言换成

\[\exists \delta > 0 ,\forall x(-\delta < x - x_0 < 0) \]

当然，括号里的不等式你也可以写成 \(x_0 - \delta < x < x_0\)。

👈右极限

\[\displaystyle\lim_{x\to x_0+}f(x) = A \]

可以参考左极限，我就不详细说了 (@_@)。

📜性质

以下内容最好看一看证明。
证明我只拿 \(x_0, A\) 都有限的双侧极限的情况举例，其他的请读者自行尝试（\(By\ yourself!\)）。

\(1.\) 极限唯一

我们采用反证法。
假设 \(f(x)\) 在 \(x_0\) 的极限有 \(A, B\)（如果有多个，取其中每两个一组）。
因此

\[\forall \varepsilon > 0, \exists \delta_1 > 0, \forall x(0 < |x - x_0| < \delta) : |f(x) - A| < \dfrac{\varepsilon}{2} \]

且

\[\forall\varepsilon > 0, \exists\delta_2 > 0, \forall x(0 < |x - x_0| < \delta) : |f(x) - B| < \dfrac{\varepsilon}{2} \]

（注意，这里有个小 \(trick\)，就是把 \(\varepsilon\) 变为任意一个常数倍（或者取幂），请读者思考一下为什么可以这样。）
然后我们取 \(\delta = \min\{\delta_1, \delta_2\}\)。
这个时候 \(\forall\varepsilon > 0,\forall x(0 < |x - x_0| < \delta)\)，两个不等式就都成立了。
于是

\[|A - B| = |(A - f(x)) + (f(x) - B)|\leq |f(x) - A| + |f(x) - B| < \dfrac{\varepsilon}{2} + \dfrac{\varepsilon}{2} = \varepsilon \]

（注意，这里也有一个小 \(trick\)，就是加上一个数再减去一个数，然后使用 三角不等式，这个方法还挺常用的。）
由于 \(\varepsilon\) 可以无限接近于 \(0\)，所以 \(A = B\)。
可能有的读者对上面这句话比较疑惑，我们也可以简单说明一下。
不妨令 \(g(x) = A\)，则

\[\forall\varepsilon > 0, \exists\delta > 0, \forall x(0 < |x - x_0| < \delta) : |g(x) - B| < \varepsilon \]

即

\[\displaystyle\lim_{x\to x_0} g(x) = B \]

而 \(g(x)\) 是一个常函数，在任意一个点的值都是 \(A\)，所以它在 \(x_0\) 的极限也是 \(A\)（这个也可以利用极限的定义证）。
因此得到 \(A = B\)。
所以得到极限唯一。

\(2.\) 局部保序性

即若 \(\displaystyle\lim_{x\to x_0}f(x) = A\)，\(\displaystyle\lim_{x\to x_0}g(x) = B\)，且 \(A > B\)，则存在 \(\delta > 0\)，使得当 \(0 < |x - x_0| < \delta\) 时，有

\[f(x) > g(x) \]

同极限唯一的证明方法一样，我们取 \(\delta = \min\{\delta_1, \delta_2\}\)（以后就不做说明了），有

\[\forall\varepsilon > 0, \exists\delta > 0, \forall x(0 < |x - x_0| < \delta):|f(x) - A| < \varepsilon, |g(x) - B| < \varepsilon \]

我们不妨令 \(\varepsilon = \dfrac{A - B}{2}\)。
由上面两个不等式，得到 \(f(x) > \dfrac{A + B}{2}, g(x) < \dfrac{A + B}{2}\)，即

\[f(x) > g(x) \]

由此可以得到一些（看上去有些无聊🫩的）推论。

推论 \(1\)

我们不妨令 \(\displaystyle\lim_{x\to x_0}f(x) = A\not= 0\)，\(g(x) = 0\)。

当 \(A > 0\) 时，由

\[f(x) > \dfrac{A + B}{2} > g(x) \]

得到

\[f(x) > \dfrac{A}{2} > 0 \]

同理，当 \(A < 0\) 时，得到

\[f(x) < \dfrac{A}{2} < 0 \]

所以

\[|f(x)| > \dfrac{|A|}{2} > 0 \]

这表明若 \(f(x)\) 在 \(x_0\) 的极限不是 \(0\) 时，若 \(x\) 充分接近 \(x_0\)，则 \(f(x)\) 不会离 \(0\) 太近（“对 \(\dots\) 吧 \(\dots\)”\(said\) 我的可可爱爱的同学）。

推论 \(2\)

由反证法，得到若 \(\displaystyle\lim_{x\to x_0}f(x) = A\)，\(\displaystyle\lim_{x\to x_0}g(x) = B\)，且存在 \(\delta > 0\)，使得当 \(0 < |x - x_0| < \delta\) 时，有

\[f(x) \leq g(x) \]

则 \(A\leq B\)。
注意，这里不能是 \(A < B\)（即使我们把条件改成 \(f(x) < g(x)\)）。
至于为什么，大家可以自己尝试举一个例子。

推论 \(3\)

局部有界（不会无限地变大或者变小）。
即若 \(\displaystyle\lim_{x\to x_0}f(x) = A\)，则存在 \(m, M\in \mathbb{R}\) 和 \(\delta > 0\)，使得对于任意满足 \(0 < |x - x_0| < \delta\) 的 \(x\)，有

\[m < f(x) < M \]

证明的话 \(\dots\) 很简单！
只需要取 \(m < A\)，\(M > A\)，\(g(x) = m\) 和 \(h(x) = M\) 就可以证明。
\(By\ the\ way\)，取 \(l = \max\{|m|, |M|\}\)，则

\[|f(x)| < l \]

\(3.\) 夹逼性

如果 \(\exists \delta_0 > 0, \forall x(0 < |x - x_0| < \delta_0)\)，有

\[g(x) \leq f(x) \leq h(x) \]

且

\[\lim_{x\to x_0}g(x) = \lim_{x\to x_0}h(x) = A \]

则

\[\lim_{x\to x_0}f(x) = A \]

这个看起来似乎很有道理，对吧。
但是怎么证明呢？
有的时候没有思路了可以直接把极限的定义写出来。

\[\forall\varepsilon > 0,\exists\delta_1 > 0, \forall x(0 < |x - x_0| < \delta_1) : |g(x) - A| < \varepsilon \]

且

\[\forall\varepsilon > 0,\exists\delta_2 > 0, \forall x(0 < |x - x_0| < \delta_2) : |h(x) - A| < \varepsilon \]

取 \(\delta = \min\{\delta_0, \delta_1, \delta_2\}\)。
得到

\[\begin{align*} A - \varepsilon < g(x) \\ h(x) < A + \varepsilon \end{align*} \]

又由 \(g(x) < f(x) < h(x)\) 得，

\[A - \varepsilon < f(x) < A + \varepsilon \]

即

\[|f(x) - A| < \varepsilon \]

即

\[\lim_{x\to x_0}f(x) = A \]

这条性质不仅看上去很有意思，实际上也很有用😜。

🧮四则运算

若 \(\displaystyle\lim_{x\to x_0} f(x) = A,\lim_{x\to x_0}g(x) = B\).
证明方式全部用到 三角不等式。
\(How\ old\ are\ you?\)（怎么老是你？😑）

➕/➖加减法

数学里的加法和减法似乎差不多 \(\dots\)

\[\displaystyle\lim_{x\to x_0}(af(x) + bg(x)) = aA + bB \]

其中 \(a, b\) 为常数，且不同时为 \(0\)。
证明：

\[\forall \varepsilon > 0, \exists\delta > 0, \forall x(0 < |x- x_0| < \delta):|f(x) - A| < \varepsilon,|g(x) - B| < \varepsilon \]

因此

\[|af(x) - aA + bg(x) - bB| = |a(f(x) - A) + b(g(x) - B)|\leq |a||f(x) - A| + |b||g(x) - B| < (|a| + |b|)\varepsilon \]

得证。
可能有朋友会感到疑惑，为什么 \(<(|a| + |b|)\varepsilon\) 可以说明极限成立，不应该是 \(<\varepsilon\) 吗。
这是因为每一个 \((|a| + |b|)\varepsilon\) 都有一个 \(\varepsilon\) 和它对应。
如果你实在没法理解，你也可以把

\[\forall \varepsilon > 0, \exists\delta > 0, \forall x(0 < |x- x_0| < \delta):|f(x) - A| < \varepsilon,|g(x) - B| < \varepsilon \]

改为

\[\forall \varepsilon > 0, \exists\delta > 0, \forall x(0 < |x- x_0| < \delta):|f(x) - A| < \dfrac{\varepsilon}{|a| + |b|},|g(x) - B| < \dfrac{\varepsilon}{|a| + |b|} \]

你就可以得到 \(< \varepsilon\) 了。
以后我就默认 \(< \lambda\varepsilon\)（\(\lambda\) 为 \(> 0\) 的常数）也能说明极限成立了。

✖️乘法

\[\displaystyle\lim_{x\to x_0}(f(x)g(x)) = AB \]

\(f(x), g(x)\) 都不是 \(0\)。
证明：
由局部保序性的推论 \(3\) 知，存在 \(l > 0,\delta_0 > 0\)，使得对于任意满足 \(0 < |x - x_0| < \delta_0\) 的 \(x\)，有 \(|g(x)| < l\)。
又

\[\forall \varepsilon > 0, \exists\delta_1 > 0, \forall x(0 < |x - x_0| < \delta_1):|f(x) - A| < \varepsilon,|g(x) - B| < \varepsilon \]

取 \(\delta = \min\{\delta_0, \delta_1\}\)。
则

\[|f(x)g(x) - AB| = |g(x)(f(x) - A) + A(g(x) - B)|\leq|g(x)||f(x) - A| + |A||g(x) - B| < (l + |A|)\varepsilon \]

得证。

➗除法

\[\displaystyle\lim_{x\to x_0}\left(\dfrac{f(x)}{g(x)}\right) = \left(\dfrac{A}{B}\right) \]

\(g(x),B\) 当然都不为 \(0\) 了！
证明：
由局部保序性的推论 \(2\) 得到，存在 \(\delta_0 > 0\)，使得对于任意满足 \(0 < |x - x_0| < \delta_0\) 的 \(x\)，有 \(|g(x)| > \dfrac{|B|}{2}\)，即 \(\dfrac{1}{|g(x)|} < \dfrac{2}{|B|}\)。
又

\[\forall \varepsilon > 0, \exists\delta_1 > 0, \forall x(0 < |x - x_0| < \delta_1):|f(x) - A| < \varepsilon,|g(x) - B| < \varepsilon \]

取 \(\delta = \min\{\delta_0, \delta_1\}\)。
则

\[\left|\dfrac{f(x)}{g(x)} - \dfrac{A}{B}\right| = \left|\dfrac{B(f(x) - A) + A(B - g(x))}{g(x)B}\right|< 2\left|\dfrac{B(f(x) - A) + A(B - g(x))}{B^2}\right| \]

然后得到（大家模仿我前面的过程自己推吧。）

\[\left|\dfrac{f(x)}{g(x)} - \dfrac{A}{B}\right| < \dfrac{2(|A| + |B|)}{B^2}\varepsilon \]

代数运算请自行验证
——《普林斯顿微积分读本》