第一次作业:深度学习基础
【第一部分】视频学习心得及问题总结
1、总结
(1)绪论
人工智能的现状
随着技术的发展和社会不断扩大的需求,各国对人工智能领域均展开了如火如荼的军备竞赛,要想在人工智能发展中夺得先机,就需要加速对人工智能方面人才的培养。当下世界范围内,人工智能方面的人才缺口是非常巨大的,这是挑战,也是机遇。对此我国教育部也出台了一系列文件,提出到2020年为止,要建设100个“人工智能+”特色专业,50个人工智能研究院。

人工智能的发展
人工智能,即使一部机器像人一样进行感知、认知、决策、执行的人工程序或系统,这一概念首次诞生于1956年的美国达特茅斯会议,这一会议标志着人工智能的诞生。期间,国际学术界人工智能研究潮流兴起,罗素《数学原理》被算法全部证明,学术交流频繁。
然而,到1969年,作为主要流派的连接主义与符合主义进入消沉,四大预言遥遥无期,在计算能力的限制下,国家及公众信心持续减弱,人工智能发展陷入瓶颈。直到1975年,BP算法开始研究,第五代计算机开始研制,专家系统的研究和应用艰难前行,半导体技术发展,计算机成本和计算能力逐步提高,人工智能才逐渐开始突破。1986年,BP网络实现,神经网络得到广泛认知,基于人工神经网络的算法研究突飞猛进;计算机硬件能力快速提升;互联网构建,分布式图络降低了人工智能的计算成本。
2006年,深度学习被提出,人工智能算法产生突破性发展;2010年,移动互联网发展,人工智能应用场景开始增多;2012年,深度学习算法在语言和视觉识别上实现突破,同年融资规模开始快速增长,人工智能进入商业化高速发展阶段。今日我们看到的大部分人工智能产品都是基于两种数理基础,逻辑演绎或归纳总结。他们分别基于逻辑学和统计学。

机器学习
机器学习最常用的定义是:计算机系统能够利用经验提高自己的性能,其本质是一个基于经验数据的函数估计问题,从统计学角度来说,即提取重要模式、趋势,并理解数据。机器学习分为三个步骤,即确定假设空间,确定目标函数,以及求解模型参数。第一步是对问题的建模。根据不同的分类标准,机器学习的模型可以有很多种不同的表达方式。

按数据标记来分,可分为监督模型与无监督模型。无监督学习的样本没有标记,它从数据中学习模式,适用于描述数据。而监督学习的样本具有标记(输出目标),它从数据中学习标记分界面(输入—输出的映射函数),适用于预测数据标记。
而从数据分布来看,参数模型对数据分布进行假设,待求解的数据模式/映射可以用一组有限且固定数目的参数进行刻画。而非参数模型不对数据分布进行假设,数据的所有统计特性都来源于数据本身。
根据不同的建模对象,还可分为判别模型和生成模型。生成模型对输入 X 和输出 Y 的联合分布P(X,Y)建模。而判别模型对已知输入 X 条件下输出 Y 的条件分布P(YIX)建模。
深度学习
-
什么是深度学习?
总的来说 人工智能>机器学习>深度学习。深度学习是实现人工智能的一种方式,他运用了深度神经网络,故叫做机器学习
-
为什么要用机器学习?
举个例子,在前深度学习时代,图像识别我们需要花费大量的时间去标注图像,绞尽脑汁地选择设计图像的特征,然后训练和测试,在一个稍微大点的问题中往往会花费数月甚至是数年的时间。
而在深度学习时代在标注完图形后,计算机可以代替我们优化模型,大大缩短时间
神经网络的发展
在1998年提出卷积网络后,在之后的十年里,神经网络一直没有较大的发展,一直到2012年,随着大规模训练,gpu的引入,神经网络得到了大的发展。大体分为了4条线,他们分别是网络加深,增强卷积模块功能,从分类任务到检测任务,增加新的功能单元,正是这些方法的引入,在2015年,深度学习的错误率首次低于人类
(2)深度学习概述
浅层神经网络
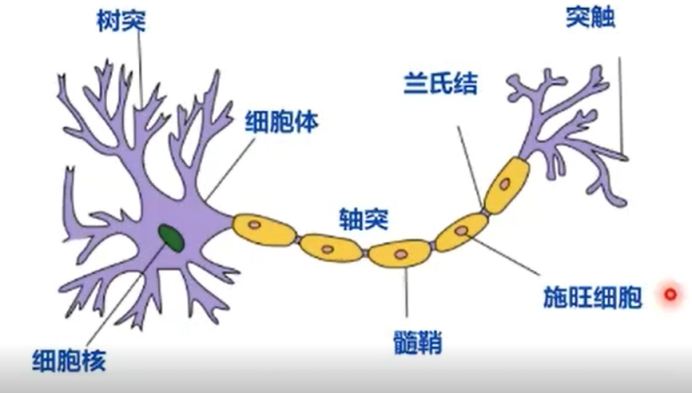
- 生物神经元:
-
每个神经元都是一个多输入单输出的信息处理单元
-
神经元具有空间整合和时间整合特性
-
神经元输入分兴奋性输入和抑制性输入两种类型
-
神经元具有阈值特性
1和2模拟多输入信号进行累加
3权值w正负模拟兴奋和抑制,大小模拟强度
4当输入和超过阈值时神经元被激活
单层感知器
单层感知器基本与M-P神经元结构基本一致,但单层感知器是可以学习人工神经网络
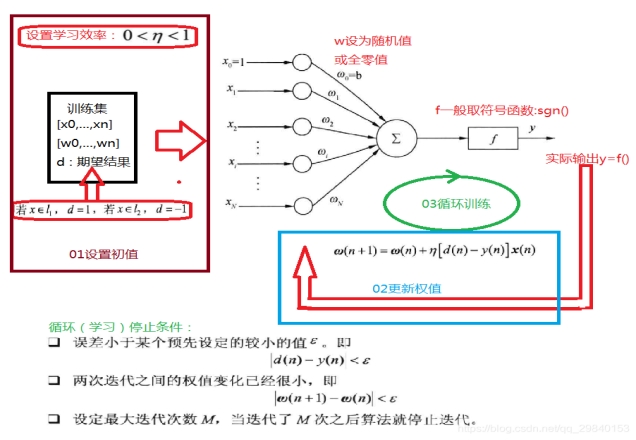
多层感知器
前言:Minsky批判单感知器无法解决异或(XOR)问题
---> 叠加多层感知器,用于解决异或这类非线性问题。
例子:多层感知器解决异或非(XNOR)问题
a XNOR b = NOT(a XOR b) = (a AND b) OR ((NOT a ) AND (NOT b))
已知单层感知器可实现 AND、NOT和 OR功能

单层感知器叠加之后实现了异或问题:



解决了单层感知器无法线性分隔异或问题的情况,用多层感知器实现了非线性分隔。
万有逼近定理
如果一个隐层包含足够多的神经元,三层前馈神经网络(输入-隐层-输出)能够以任意精度逼近任意连续函数。
当隐层足够宽时,双隐层感知器(输入-隐层1-隐层2-输出)可以逼近任意非连续性函数.
其中每一层公式都是 $ \mathbf{y}=a(w*\mathbf{x}+b)$ ,其中
$ w*\mathbf{x}$:实现数据的升/降维,放大/缩小,旋转。(线性变换)
$ +b$ :实现数据的平移。(线性变换)
\(a(.)\) : 实现数据的弯曲。 (非线性变换,激活函数实现)

综上:增加节点数 : 增加维数,增加线性转换能力 。增加层数:增加激活函数(在神经元处)次数,增加非线性转换能力。

反向传播
多层神经网络 ->看成复合的非线性多元函数: \(F(.) = X->Y\)
\(F_n(x)= f_{n}(f_{n-1}...f_3(f_2(f_1(x)*\theta_1+b_1)*\theta_2+b_2)...+b_{n-1})+b_n\)
给定训练数据\(\{X^i,Y^i\} _{i=1:N}\),希望损失\(\sum_{i=1}^mloss(F(x^i),y^i)\)尽可能小,需要在训练过程中对误差反向传播。误差信息回传重新调整神经元。
方法:利用梯度下降的方法,延负梯度方向使得函数值下降。

三层前馈神经网络反向传播的公式推导如下:

梯度消失
误差反向传播理论上可以达到训练目的,实现对参数的调节,但是随着深度的增加,如下图中的所示公式,在激活函数为sigmoid函数的时候,激活函数导数的值太小,在0到0.25之间,在反向传播时连乘求出的偏导数太小,导致误差无法传播到前面的层,从而容易陷入到局部极值的情形,难以进行训练。


为解决梯度消失问题->进行逐层预训练。
逐层预训练

神经网络不是凸问题,且局部极小值数量随神经网络层数成倍增长。但若找到一个很好的初始值,就可能找到一个全局的极小值
梯度消失若有一个不错的初始函数,也可得到一个不错的结果
权重初始化:逐层预训练每次训练一个三层的网络,将中间层累计到后面,再继续训练下一层网络。开始选的参数不太差,得到的结果更容易收敛

1.不同的初始值会收敛到不同的极小值
2.逐层预训练得到的极小值是相对收敛的,不容易得到更差的点
逐层预训练步骤

自编码器
传统的监督问题,给定输入,得到输出,可以与目标对比计算损失

流程图中间的编码code就是我们想得到的特征,是一种有监督的学习(将自己的输入当成输出)

三层:输入层、隐含层、输出解码层。
找到中间的编码就不需要输入层了,因为通过中间的编码就可以重构出相似的输入了(中间的隐含层就是对”输入“的表示,可以最大程度代表输入信号)
自编码器最初被用来降维

自编码器是一个编码和解码的框架

注意:自编码器也不一定是三层,但基本上是先编码再解码的过程
自编码器作为隐层串联,所有层预训练完成后进行基于监督学习的网络微调

受限玻尔兹曼机(RBM)
结构模型
- RBM是两层可见网络,包含隐藏层h和可见层v(也叫输入层),其结构是一个二分图。
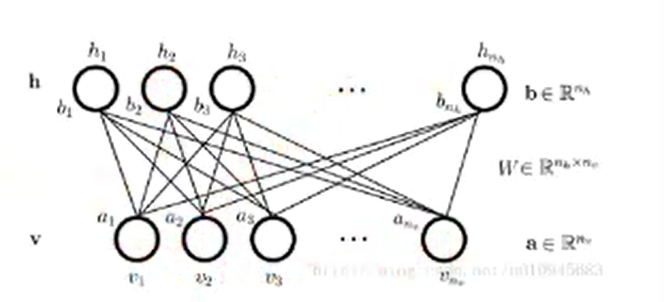
- RBM基于概率分布定义,高层表示为底层特征的条件概率,输出只有两种状态,用0/1表示。

两个方向权重w共享,但偏置不同。
条件概率建模
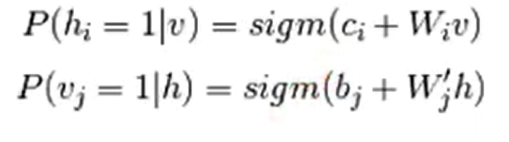
- sigm函数推导
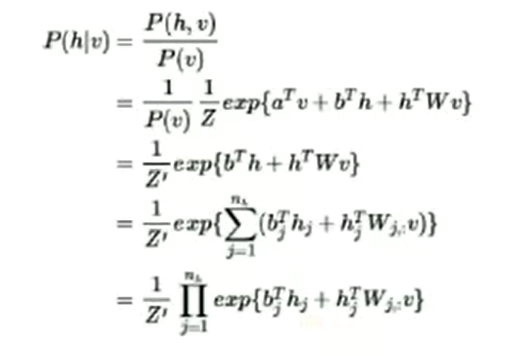
假设是标准波尔兹曼分布:所有节点是二进制变量(0,1)

训练优化
- RBM基于最大似然,能量函数偏导无法直接计算,基于采样方法进行估计。
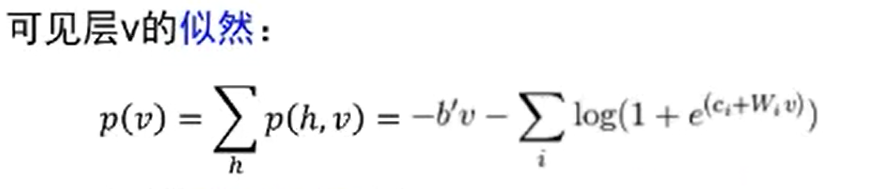
最大似然的梯度下降求解:
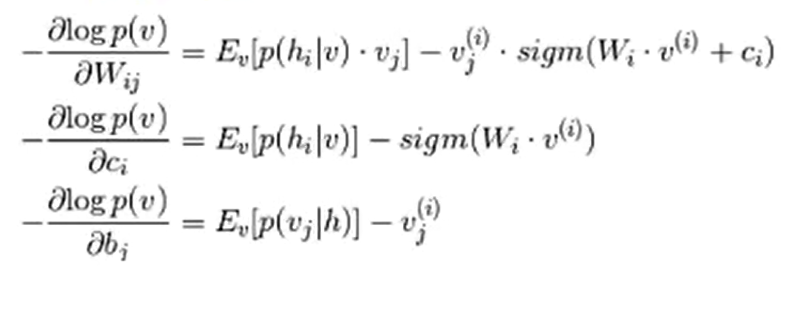
RBM到DBN(深度信念网络)
一个DBN模型由若干个RBM堆叠而成,最后加一个监督层。
训练过程由低到高逐层训练:
①最底部RBM以原始输入数据训练
②将底部RBM抽取的特征作为顶部RBM的输入继续训练
③重复这个过程训练尽可能多的RBM层
④基于监督信息通过全局优化算法对网络进行微调,使模型收敛
2、疑问
| 成员 | 问题 |
|---|---|
| 伍政谦 | 新的激活函数ReLu为什么在负无穷到0部分时函数值是0,有什么原因吗? |
| 朱笔锋 | 逐层预训练中若有多个相同的极小值,如何确定较好的初始值? |
| 邵骏飞 | 目前知识图谱和神经网络分别在那些方面占据了优势? |
| 任博达 | 单层感知器如何确定权值? |
| 习泽坤 | 万有逼近定律是怎么推导的? |
| 郭冉 | 受限玻尔兹曼机为什么现实中不实用? |




 浙公网安备 33010602011771号
浙公网安备 33010602011771号