第二次作业报告

代码练习总结

1. 什么是pytorch？

　　PyTorch是一个python库，它主要提供了两个高级功能：

• GPU加速的张量计算
• 构建在反向自动求导系统上的深度神经网络

2. pytorch基础练习

　1. 定义数据

　　一般定义数据使用torch.Tensor ， tensor的意思是张量，是数字各种形式的总称

　2.定义操作　 

　　凡是用Tensor进行各种运算的，都是Function

　　最终，还是需要用Tensor来进行计算的，计算无非是

• 基本运算，加减乘除，求幂求余
• 布尔运算，大于小于，最大最小
• 线性运算，矩阵乘法，求模，求行列式

x = torch.empty(5,3)
print(x)
x = torch.rand(5,3)
print(x)
x = torch.zeros(5,3,dtype=torch.long)
print(x)
y = x.new_ones(5,3)   #tensor new_* 方法，利用原来tensor的dtype，device
print(y)
z = torch.randn_like(x, dtype=torch.float)    # 利用原来的tensor的大小，但是重新定义了dtype
print(z)

 

3. 螺旋数据分类

　　1.线性数据分类

代码如下

learning_rate = 1e-3
lambda_l2 = 1e-5

# nn 包用来创建线性模型
# 每一个线性模型都包含 weight 和 bias
model = nn.Sequential(
    nn.Linear(D, H),  #D:每个样本的特征维度 H:神经网络里隐层单元的数量
    nn.Linear(H, C)   #C 样本的类别
)
model.to(device) # 把模型放到GPU上

# nn 包含多种不同的损失函数，这里使用的是交叉熵（cross entropy loss）损失函数
criterion = torch.nn.CrossEntropyLoss()

# 这里使用 optim 包进行随机梯度下降(stochastic gradient descent)优化
optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate, weight_decay=lambda_l2)

# 开始训练
for t in range(1000):
    # 把数据输入模型，得到预测结果
    y_pred = model(X)
    # 计算损失和准确率
    loss = criterion(y_pred, Y)         #沿着第二个方向（相当于二维列表横轴方向）提取最大值。最大的那个值存在 score 中
    score, predicted = torch.max(y_pred, 1)   #所在的位置（即第几列的最大）保存在 predicted 中。
    acc = (Y == predicted).sum().float() / len(Y)
    print('[EPOCH]: %i, [LOSS]: %.6f, [ACCURACY]: %.3f' % (t, loss.item(), acc))
    display.clear_output(wait=True)

    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

 

 

 

 

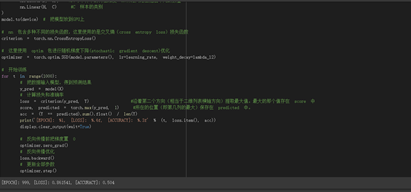
由运行结果我们可以看出，线性数据分类的准确率很低，只有 50%左右

　　2.构建两层神经网络分类

代码如下

learning_rate = 1e-3
lambda_l2 = 1e-5

# 这里可以看到，和上面模型不同的是，在两层之间加入了一个 ReLU 激活函数
model = nn.Sequential(
    nn.Linear(D, H),
    nn.ReLU(),
    nn.Linear(H, C)
)
model.to(device)

# 下面的代码和之前是完全一样的，这里不过多叙述
criterion = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate, weight_decay=lambda_l2) # built-in L2

# 训练模型，和之前的代码是完全一样的
for t in range(1000):
    y_pred = model(X)
    loss = criterion(y_pred, Y)
    score, predicted = torch.max(y_pred, 1)
    acc = ((Y == predicted).sum().float() / len(Y))
    print("[EPOCH]: %i, [LOSS]: %.6f, [ACCURACY]: %.3f" % (t, loss.item(), acc))
    display.clear_output(wait=True)
    
    # zero the gradients before running the backward pass.
    optimizer.zero_grad()
    # Backward pass to compute the gradient
    loss.backward()
    # Update params
    optimizer.step()

 

 

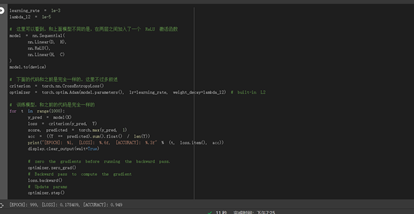
由此我们可以看出，经过优化之后，准确率大大提高了

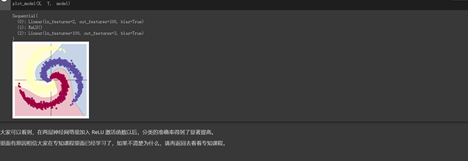
 运行结果可视化如图