数竞定理 & 结论大全

• 代数篇
  • 0x01. 方程
  • 0x02. 多项式
  • 0x03. 不等式
  • 0x04. 集合
• 函数篇
  • 0x01. 二次函数
  • 0x02. 一般函数
  • 0x03. 特殊函数
• 数论篇
  • 0x01. 定义
  • 0x02. 基本结论
  • 0x03. 整除分析
  • 0x04. 素数幂分析
  • 0x05. 不定方程
  • 0x06. 同余
  • 0x07. 进制
  • 0x08. 冷门结论 & 定理
• 组合数学篇
  • 0x01. 定义
  • 0x02. 定理 & 结论
• 几何篇
  • 0x00. 定义 & 概念
  • 0x01. 一般三角形
  • 0x02. 特殊三角形
  • 0x03. 圆
  • 0x04. 四边形
  • 0x05. 三角函数
  • 0x06. 向量
    • 定义
    • 定理

记号约定：

• \(\mathbb{P}\)：全体质数集合。
• \(a \perp b\)：直线 \(a\) 与 \(b\) 垂直；整数 \(a\) 和 \(b\) 互质。
• \(a \parallel b\)：直线 \(a\) 与 \(b\) 平行；（规定 \(\exist i \in \mathbb{N}, p \in \mathbb{P}, a = p^i\)）整数 \(p^i, b\) 满足 \(p^i \mid b, p^{i + 1} \nmid b\)。
• \(\nu_p(n)\)：质数 \(p\) 在整数 \(n\) 的质因数分解中的幂次。
• \([x^n] f(x)\)：多项式 \(f(x)\) 中 \(x^n\) 的系数。
• （Iverson 括号）\([\mathrm{P}]\)：命题 \(\mathrm{P}\) 为真时取 \(1\)，否则取 \(0\)。

有些地方还没有完工，甚至快烂尾了，在此道歉。

更新记录：

• 2025.8.11。
• 2025.8.21：
  • 增加了 Menelaus 定理。
  • 增加了 Simson 定理。
  • 增加了 Ptolemy 定理。
  • 增加了三弦共点定理。
  • 增加了广义 Ptolemy 定理。
• 2025.9.10：迁移解析几何相关内容到新的文章。

代数篇

0x01. 方程

1. 方程 \(|x - a| = b\) 的所有根的和为

\[\begin{cases} \begin{aligned} &2a, &b > 0 \\ &a, &b = 0 \\ &0 &b < 0 \end{aligned} \end{cases} \]

证明：分类讨论 \(b\) 的正负性：

• \(b > 0\)：其有 2 个解，分别为 \(x_{1, 2} = a \pm b\)，和为 \(2a\)。
• \(b = 0\)：其有 1 个解，为 \(x = a\)，和为 \(a\)。
• \(b < 0\)：其无解，和为 \(0\)。

故原命题得证。

思路：

Q1：方程 \(|x - 2| = 2.5\) 的所有根之和为多少？
A1：为 4。

Q2：方程 \(|x - m| = 2.5\) 的所有根之和为多少？
A2：为 \(2m\)。

Q3：方程 \(|x - m| = 0\) 的所有根之和为多少？
A3：为 \(m\)。

Q4：方程 \(|x - m| = n\) 的所有根之和为多少？
A4：为

\[\begin{cases} \begin{aligned} &2a, &b > 0 \\ &a, &b = 0 \\ &0 &b < 0 \end{aligned} \end{cases} \]

1.1. 对于两个向量 \(\vec{a}, \vec{b}\)，有 \(|\vec{a}| + |\vec{b}| \ge |\vec{a} + \vec{b}|\)。

证明：考虑向量 \(\vec{a}, \vec{b}, \vec{a} + \vec{b}\) 有没有组成三角形：

• 如果有，则 \(|\vec{a}| + |\vec{b}| > |\vec{a} + \vec{b}|\)（三角形的两边之和大于第三边）。
• 如果没有，则 \(|\vec{a}| + |\vec{b}| = |\vec{a} + \vec{b}|\)。

故 \(|\vec{a}| + |\vec{b}| \ge |\vec{a} + \vec{b}|\)。

2. 若二次式 \(f(x)\) 为完全平方式，那么其判别式 \(\Delta = 0\)。

证明：设 \(f(x) = a(x - r)^2\)，则其两根为 \(x_{1, 2} = r\)。故 \(\Delta = 0\)。

2.1. 若二次式 \(f(x)\) 的判别式 \(\Delta = 0\)，那么其为完全平方式。

证明：设其两根为 \(x_{1, 2} = r\)，则一定可以找到一个常数 \(a \not = 0\)，使得 \(f(x) = a(x - r)^2\) 为完全平方式。

3. 若二次式 \(f(x)\) 为完全平方式，那么其判别式 \(\Delta = 0\)。

证明：设 \(f(x) = a(x - r)^2\)，则其两根为 \(x_{1, 2} = r\)。故 \(\Delta = 0\)。

3.1. 若二次式 \(f(x)\) 的判别式 \(\Delta = 0\)，那么其为完全平方式。

证明：设其两根为 \(x_{1, 2} = r\)，则一定可以找到一个常数 \(a \not = 0\)，使得 \(f(x) = a(x - r)^2\) 为完全平方式。

4. \(\displaystyle x^{2^n} - 1 = (x - 1) \prod_{j = 0}^{n - 1} (x^{2^j} + 1)\)。

证明：等号右边为

\[\begin{aligned} & \ (x - 1)(x + 1)(x^2 + 1)(x^4 + 1) \cdots (x^{2^{n - 1}} + 1) \\ =& \ (x^2 - 1)(x^2 + 1)(x^4 + 1) \cdots (x^{2^{n - 1}} + 1) \\ =& \ (x^4 - 1)(x^4 + 1) \cdots (x^{2^{n - 1}} + 1) \\ \vdots \\ =& \ x^{2^n} - 1 \end{aligned} \]

等于左边，故原命题得证。

5. 方程 \(|x - a| = b\) 有 \(2[b > 0] + [b = 0]\) 个解。

证明：分类讨论 \(b\) 的正负性：

• \(b > 0\)：其有 2 个解，分别为 \(x_{1, 2} = a \pm b\)，与原命题吻合。
• \(b = 0\)：其有 1 个解，为 \(x = a\)，与原命题吻合。
• \(b < 0\)：其无解，与原命题吻合。

故原命题得证。

0x02. 多项式

1. 对于一个多项式 \(f(x)\)，若其分别能被两个一次多项式 \(x - k_1, x - k_2\) 整除（满足 \(k_1 \not = k_2\)），那么其就能被 \((x - k_1)(x - k_2)\) 整除。

证明（余数定理）：设 \(f(x) = (x - k_1) \cdot q_1(x)\)，则 \(f(k_2) = (k_2 - k_1) \cdot q_1(k_2) = 0\)（因为 \(f(x)\) 被 \((x - k_2)\) 整除）。因为 \(k_1 \not = k_2\)，所以 \(q_1(k_2) = 0\)。则 \(q_1(x) = (x - k_2) \cdot q_2(x), f(x) = (x - k_1)(x - k_2) \cdot q_2(x)\)。原命题得证。

2.（欧拉公式）\(x^3 + y^3 + z^3 - 3xyz = (x + y + z)(x^2 + y^2 + z^2 - xy - yz - zx)\)。

2.1. \(x^2 + y^2 + z^2 - xy - yz - zx = 0 \implies x = y = z\)。

证明：因为 \(x^2 + y^2 + z^2 - xy - yz - zx = \dfrac{(x - y)^2 + (y - z)^2 + (z - x)^2}{2} = 0\)，所以 \(x - y = y - z = z - x = 0 \implies x = y = z\)。证毕。

3. 设 \(f(x)\) 为整系数多项式，则 \(m - n \mid f(m) - f(n)\)。

证明：设 \(f(m) - f(n) = \sum \limits_{i = 1}^{\deg f} a_i (m^i - n^i)\)。

因为 \(\forall i \in \mathbb{N}, m - n \mid m^i - n^i\)，所以 \(f(m) - f(n)\) 的每一项都被 \(m - n\) 整除。

故证毕。

0x03. 不等式

1.（绝对值不等式）对于实数 \(a, b\)，有 \(|a| + |b| \ge |a + b| \ge ||a| - |b||\)。其中在 \(a, b\) 同号时第一个不等号取等，在 \(a, b\) 异号时第二个不等号取等。

证明：设 \(a > b\)，考虑 \(a, b\) 的符号：

• \(a, b\) 同号：\(|a| + |b| = |a + b|\)，\(|a + b| > ||a| - |b||\)。
• \(a, b\) 异号：\(|a| + |b| = b - a = |a - b| > |a + b|\)，\(|a + b| = |a| - |b| = ||a| - |b||\)。

原命题得证。

2.（均值不等式）\(H_n \le G_n \le A_n \le Q_n\)，其中：

• \(x_1, x_2, \cdots, x_n \in \R_{\ge 0}\)。
• \(H_n = \dfrac{n}{\sum_{i = 1}^n x_i^{-1}}\)，\(G_n = \sqrt[n]{\prod \limits_{i = 1}^n x_i}\)，\(A_n = \dfrac{\sum_{i = 1}^n x_i}{n}\)，\(Q_n = \sqrt{\dfrac{\sum_{i = 1}^n x_i^2}{n}}\)。

证明：考虑以下函数：

\[D(r) = \begin{cases} \left( \dfrac{x_1^r + x_2^r + \cdots + x_n^r}{n} \right)^{1/r}, &r \neq 0 \\ (x_1 x_2 \cdots x_n)^{1/n}, &r = 0 \\ \max(x_1, x_2, \cdots, x_n), &r = \infty \\ \min(x_1, x_2, \cdots, x_n) &r = -\infty \end{cases} \quad (\nexists x_i = 0) \]

可以发现，\(H_n = D(-1), G_n = D(0), A_n = D(1), Q_n = D(2)\)。

则只需证 \(D(-1) \le D(0) \le D(1) \le D(2)\)，下证该函数单调递增。

......

3.（Bernoulli 不等式）\((1 + a)^n \ge 1 + an \quad (n \ge 0)\)。

证明（归纳法）：当 \(n = 1\) 时，\((1 + a)^1 \ge 1 + a\) 显然成立。

下面证明当 \((1 + a)^n \ge 1 + na\) 成立时，\((1 + a)^{n + 1} \ge 1 + (n + 1)a\) 成立。

我们发现，只需证明 \((1 + a)^n \ge \dfrac{1 + (n + 1) a}{1 + a}\) 即可。

又因为 \((1 + a)^n \ge 1 + na\)，所以只需证明 \(\dfrac{1 + (n + 1) a}{1 + a} \le 1 + na\)。

则：

\[\begin{aligned} na^2 \ge 0 &\implies 1 + (n + 1) a + na^2 \ge 1 + (n + 1) a \\ &\implies (1 + a)(1 + na) \ge 1 + (n + 1) a \\ &\implies 1 + na \ge \dfrac{1 + (n + 1) a}{1 + a} \\ &\implies (1 + a)^n \ge 1 + na \ge \dfrac{1 + (n + 1) a}{1 + a} \\ &\implies (1 + a)^{n + 1} \ge 1 + (n + 1) a \end{aligned} \]

证毕。

4.（权方和不等式）对于任意的 \(2n\) 个正实数 \(a_1, a_2, \cdots, a_n, b_1, b_2, \cdots, b_n\) 以及常数 \(m \in (-\infty, -1) \cup (0, +\infty)\)，都有：

\[\sum_{i = 1}^n \dfrac{a_i^{m + 1}}{b_i^m} \ge \dfrac{\left( \sum_{i = 1}^n a_i \right)^{m + 1}}{\left( \sum_{i = 1}^n b_i \right)^m} \]

0x04. 集合

1.（De Morgan 定律）\(\complement_U (A \cup B) = \left( \complement_U A \right) \cap \left( \complement_U B \right), \complement_U (A \cap B) = \left( \complement_U A \right) \cup \left( \complement_U B \right)\)。

2. \(A \cup (B \cap C) = (A \cup B) \cap (A \cup C), A \cap (B \cup C) = (A \cap B) \cup (A \cap C)\)。

3.（容斥原理）\(\displaystyle \left| \bigcup_{i = 1}^n S_i \right| = \sum_{1 \le i \le n} |S_i| - \sum_{1 \le i < j \le n} |S_i \cap S_j| + \sum_{1 \le i < j < k \le n} |S_i \cap S_j \cap S_k| - \cdots + (-1)^{n - 1} \left| \bigcap_{i = 1}^n S_i \right| = \sum_{k = 1}^n (-1)^{k - 1} \left( \sum_{1 \le i_1 < i_2 < \cdots < i_k \le n} \left| \bigcap_{j = 1}^k S_{i_j} \right| \right)\)。

函数篇

0x01. 二次函数

1. 二次函数 \(f(x) = a(x - h)^2 + b\) 的顶点为 \((h, b)\)。

证明：该二次函数的顶点 \((u, v)\) 满足：

\[\begin{cases} f'(u) = 0 \\ f(u) = v \end{cases} \]

对其求导：

\[f'(x) = 2a(x - h) \]

则 \(f'(u) = 0 \implies u = h\)，代入 \(f(x)\) 得 \(v = f(h) = b\)。

故原命题得证。

1.1. 若二次函数 \(f(x)\) 的顶点为 \((h, b)\)，那么 \(f(x) = a(x - h)^2 + b \quad (a \neq 0)\)。

证明：设 \(f(x) = a(x - u)^2 + v\)，则其顶点为 \((u, v) = (h, b)\)，故 \(u = h, v = b, f(x) = a(x - h)^2 + b\)。

故原命题得证。

0x02. 一般函数

1. 设 \(g(x)\) 为函数 \(f(x)\) 向左平移 \(a\) 个单位长度，则 \(g(x) = f(x + a)\)。

证明 1：可以发现，点 \((x, f(x))\) 在 \(f\) 上，则其向左平移 \(a\) 个单位长度后，其坐标为 \((x - a, f(x))\) 在 \(g\) 上。

则 \(g(x - a) = f(x) \implies g(x) = f(x + a)\)。

证明 2：可以发现，点 \((x, g(x))\) 在 \(g\) 上，则其向右平移 \(a\) 个单位长度后，其坐标为 \((x + a, g(x))\) 在 \(f\) 上。

则 \(f(x + a) = g(x)\)，证毕。

2.（常用函数的单调区间）

原函数	单调区间
\(f(x) = kx + b, k > 0\)	\((-\infty, \infty) \uparrow\)
\(f(x) = kx + b, k < 0\)	\((-\infty, \infty) \downarrow\)
\(f(x) = ax^2 + bx + c, a > 0\)	\((-\infty, -\dfrac{b}{2a}) \downarrow, (-\dfrac{b}{2a}, \infty) \uparrow\)
\(f(x) = ax^2 + bx + c, a < 0\)	\((-\infty, -\dfrac{b}{2a}) \uparrow, (-\dfrac{b}{2a}, \infty) \downarrow\)
\(f(x) = \dfrac{k}{x}, k > 0\)	\((-\infty, 0) \downarrow, (0, \infty) \downarrow\)
\(f(x) = \dfrac{k}{x}, k < 0\)	\((-\infty, 0) \uparrow, (0, \infty) \uparrow\)
\(f(x) = x + \dfrac{a}{x}, a > 0\)	\((-\infty, -\sqrt{a}) \uparrow, (-\sqrt{a}, 0) \downarrow, (0, \sqrt{a}) \downarrow, (\sqrt{a}, \infty) \uparrow\)
\(f(x) = x + \dfrac{a}{x}, a < 0\)	\((-\infty, 0) \uparrow, (0, \infty) \uparrow\)

3.（奇偶函数的四则运算）

设 \(f(x)\) 与 \(g(x)\) 的定义域相同。

\(f(x)\)	\(g(x)\)	\(f(x) + g(x)\)	\(f(x) - g(x)\)	\(f(x)g(x)\)	\(\dfrac{f(x)}{g(x)}\)
偶函数	偶函数	偶函数	偶函数	偶函数	偶函数
偶函数	奇函数	-	-	奇函数	奇函数
奇函数	偶函数	-	-	奇函数	奇函数
奇函数	奇函数	奇函数	奇函数	偶函数	偶函数

4.（零点存在性定理）若连续函数 \(f(x)\) 满足 \(f(x_0) = 0\) 的充要条件是 \(\exists l < x_0 < r, f(l) \cdot f(r) < 0\)。

0x03. 特殊函数

1.（\(\log\) 的性质）

• \(\log_a(b) = \dfrac{\ln(b)}{\ln(a)}\)。
• \(\log(a) + \log(b) = \log(ab)\)。
• \(\log(a) - \log(b) = \log(a/b)\)。
• \(\log(a^x) = x \log(a)\)。
• \(\log_{a^b}(c) = \log_a(c^{1/b}) = \dfrac{1}{b} \log_a(c)\)。
• \(\log_a(b) \cdot \log_b(a) = 1\)。
• （换底公式）\(\log_a(b) = \dfrac{\log_c(b)}{\log_c(a)}\)。

数论篇

数学是科学的皇后，数论是数学的皇后。——约翰 · 卡尔 · 弗里德里希 · 高斯

0x01. 定义

1. 剩余类：对于模数 \(m\)，可以把 \(\mathbb{Z}\) 划分成 \(m\) 的集合 \(S_0, S_1, \cdots, S_{m - 1}\)（即模 \(m\) 的剩余类），其中 \(S_i = \{ x \mid x \bmod m = i \}\)。

2. 完全剩余系（完系）：从模 \(m\) 的剩余类 \(S_0, S_1, \cdots, S_{m - 1}\) 中各取一数 \(a_0, a_1, \cdots, a_{m - 1}\)，则它们构成模 \(m\) 的一个完全剩余系。

3. 缩剩余类：对于模 \(m\) 的剩余类 \(S_0, S_1, \cdots, S_{m - 1}\) 中有一些 \(S_i\)，其中 \(\forall x \in S_i, x \perp m\)。我们将这些 \(S_i\) 定义为模 \(m\) 的缩剩余类。

4. 循环节：在整数数列 \(a\) 中，设递推式为 \(a_n = f(a_{n - 1}, a_{n - 2}, \cdots, a_{n - k})\)。对于任意模数 \(m\)，记数列 \(a\) 模 \(m\) 的余数列为 \(b\)，则 \(b\) 有周期，且定义一个周期内 \(b_n\) 的值为循环节。容易发现，它的长度 \(\le m\)。

5. 逆元（模逆、乘法逆元）：若 \(a \perp m\)，则满足 \(ax \equiv 1 \pmod m\) 的 \(x\) 为 \(a\) 模 \(m\) 的逆元。记作 \(a^{-1} \pmod m\) 或 \(\dfrac{1}{a} \pmod m\)。

6. 缩剩余系（缩系）：从模 \(m\) 的缩剩余类 \(S_0, S_1, \cdots, S_{m - 1}\) 中各取一数 \(a_0, a_1, \cdots, a_{m - 1}\)，则它们构成模 \(m\) 的一个缩剩余系。

7. 幂数：形如 \(m^n\) 的数，其中 \(m, n \in \mathbb{Z}; n > 0\)。

8. 阶：对于 \(a \perp m\)，有最小的 \(k\) 使得 \(a^k \equiv 1 \pmod m\)，则定义此 \(k\) 为 \(a\) 模 \(m\) 的阶。

9. 费马数：第 \(n\) 个费马数 \(F_n = 2^{2^n} + 1\)。

10. 梅森数：梅森数 \(M_p = 2^p - 1 \quad (p \in \mathbb{P})\)。

0x02. 基本结论

1. 设正整数 \(n\) 的质因数分解为 \(n = \prod \limits_{i = 1}^k p_i^{\alpha_i}\)，\(\sigma(n)\) 表示 \(n\) 的正因数之和，则：

\[\begin{aligned} \sigma(n) &= (1 + p_1 + p_1^2 + \cdots + p_1^{\alpha_1})(1 + p_2 + p_2^2 + \cdots + p_2^{\alpha_2}) \cdots (1 + p_k + p_k^2 + \cdots + p_k^{\alpha_k}) \\ &= \prod_{i = 1}^k \dfrac{1 - p_i^{\alpha_i + 1}}{1 - p_i} \end{aligned} \]

证明：将 \(\sigma(n)\) 展开，则每一项都对应一个正因数。证毕。

2.（\(\gcd\) 的性质）设 \(d = \gcd(m, n), dm' = m, dn' = n\)，则：

• \(\gcd(m', n') = 1\)。
• \(\operatorname{lcm}(m, n) = dm'n'\)。
• \(mn = d \cdot \operatorname{lcm}(m, n) = \gcd(m, n) \cdot \operatorname{lcm}(m, n)\)。

3.（辗转相除法）\(\gcd(m, n) = \gcd(m - n, n)\)。

证明：设 \(d = \gcd(m, n)\)，则 \(d \mid m, d \mid n \implies d \mid m - n\)。下证其为最大的整数满足 \(d \mid m - n\) 且 \(d \mid n\)。

设 \(d' \mid m - n, d' \mid n, d' > d\)，则 \(d' \mid m\)，则 \(d'\) 为 \(m, n\) 的公因数，则 \(d' \le d\)，与假设矛盾！

故 \(d\) 为最大的整数满足 \(d \mid m - n\) 且 \(d \mid n\)，证毕。

4.（二项式定理）\((a + b)^n = \sum \limits_{i = 0}^n \dbinom{n}{i} a^i b^{n - i} \quad (n \in \mathbb{N})\)。

证明：对于 \(a^i b^{n - i}\) 这一项，我们需要在 \(n\) 个 \(a\) 中选 \(i\) 个，后让剩下 \(n - i\) 个用 \(b\) 补上，共有 \(\dbinom{n}{i}\) 种方案，故系数为 \(\dbinom{n}{i}\)。证毕。

5.（下取整的性质）

• \(\lfloor x \rfloor + \lfloor y \rfloor + 1 \ge \lfloor x + y \rfloor \ge \lfloor x \rfloor + \lfloor y \rfloor\)。
• \(\lfloor 2x \rfloor + \lfloor 2y \rfloor = \lfloor x \rfloor + \lfloor y \rfloor + \lfloor x + y \rfloor\)。
• \(x \ge \lfloor x \rfloor > x - 1\)。
• \(\lfloor n + x \rfloor = n + \lfloor x \rfloor \quad (n \in \mathbb{Z})\)。

6. 若数列 \(a\) 有最小周期 \(T\) 与周期 \(T'\)，则 \(T \mid T'\)。

7. 若数列 \(a\) 有周期 \(T_1, T_2\)，则它有周期 \(\gcd(T_1, T_2)\)。

证明：设 \(a\) 的最小周期为 \(T\)，则 \(T \mid T_1, T \mid T_2 \implies T \mid \gcd(T_1, T_2)\)，证毕。

0x03. 整除分析

1.（整除的性质）

• \(a \mid b \implies a \mid bc\)。（可以让右式乘某式）
• \(a \mid b, a \mid c \implies a \mid mb \pm nc\)。（可以在右式去掉左式的因数）
• \(a \mid bc, a \perp b \implies a \mid c\)。（可以在右式中去掉与左式互质的因数）
• \(ab \mid c \implies a \mid c, b \mid c\)。（可以拆左式）
• \(a \mid b \implies |a| \le |b|\)。（可以找大小矛盾）
• 更强的结论：\(a \mid b \implies |a| = |b| \ \text{or} \ |a| \le \dfrac{|b|}{2}\)。
• \(a \mid c, b \mid c, a \perp b \implies ab \mid c\)。

2. 设 \(d_1, d_2, \cdots, d_k\) 为整数 \(n\) 的所有正因数，则 \(\forall i, d_i \cdot d_{k + 1 - i} = n\)。

0x04. 素数幂分析

1.（Legendre 定理）\(\nu_p(n!) = \sum \limits_i \left \lfloor \dfrac{n}{p^i} \right \rfloor \quad (p \in \mathbb{P}, n \ge 1)\)。

证明：可以发现，\(p\) 的倍数在 \(1, 2, \cdots, n\) 中共有 \(\left \lfloor \dfrac{n}{p} \right \rfloor\) 个。

故对于 \(p^i\)，有 \(\left \lfloor \dfrac{n}{p^i} \right \rfloor\) 的贡献，对于每个 \(i\) 求和即可。

2.（Kummer 引理）定义 \(S_p(n)\) 表示 \(n\) 在 \(p\) 进制表示下的数码之和，则 \(\nu_p(n!) = \dfrac{n - S_p(n)}{p - 1} \quad (p \in \mathbb{P}, n \ge 1)\)。

证明：设 \(n = \sum \limits_{i = 0}^k a_i \cdot p^i\)。

我们可以发现，\(\dfrac{n}{p^i} = \sum \limits_{j = 0}^k a_j \cdot p^{j - i} = \sum \limits_{j = i}^{k} a_{j} \cdot p^{j - i} + \sum \limits_{j = 0}^{i - 1} a_j \cdot p^{j - i}\)。

故 \(\left \lfloor \dfrac{n}{p^i} \right \rfloor = \sum \limits_{j = i}^k a_{j} \cdot p^{j - i}\)，故：

\[\begin{aligned} \nu_p(n!) &= \sum_i \left \lfloor \dfrac{n}{p^i} \right \rfloor \\ &= \sum_{i = 0}^k \sum_{j = i}^k a_{j} \cdot p^{j - i} \\ &= \sum_{i = 0}^k \sum_{j = 0}^k [i \le j] \cdot a_j \cdot p^{j - i} \\ &= \sum_{j = 0}^k \sum_{i = 0}^k [i \le j] \cdot a_j \cdot p^{j - i} \\ &= \sum_{j = 0}^k a_j \cdot \left( \sum_{i = 0}^{j - 1} p^{j - i} \right) \\ &= \sum_{j = 0}^k a_j \cdot \dfrac{1 - p^j}{1 - p} \\ &= \dfrac{1}{1 - p} \sum_{j = 0}^k a_j - a_j \cdot p^j \\ &= \dfrac{1}{1 - p} \left( \sum_{j = 0}^k a_j - \sum_{j = 0}^k a_j \cdot p^j \right) \\ &= \dfrac{S_p(n) - n}{1 - p} \\ &= \dfrac{n - S_p(n)}{p - 1} \end{aligned} \]

证毕。

3.（Kummer 定理）定义 \(S_p(n)\) 表示 \(n\) 在 \(p\) 进制表示下的数码之和，则对于质数 \(p\) 与整数 \(m, n\)，\(\nu_p \left( \dbinom{m}{n} \right) = \dfrac{S_p(n) + S_p(m - n) - S_p(m)}{p - 1}\) 为 \(p\) 进制下 \(m - n\) 的借位次数。

4.（\(\nu\) 的性质）

设整数 \(a \ge b, k \ge 0\)，则：

• \(\nu_p(a) \pm \nu_p(b) = \nu_p(a \cdot b^{\pm 1})\)。
• \(k \cdot \nu_p(a) = \nu_p \left( a^k \right)\)。
• \(\nu_p(a \pm b) \ge \nu_p(a) \quad (\nu_p(a) = \nu_p(b))\)。
• \(\nu_p(a \pm b) = \min(\nu_p(a), \nu_p(b)) \quad (\nu_p(a) \neq \nu_p(b))\)。

5.（LTE 引理）对于正整数 \(p, x, y\) 满足 \(p \in \mathbb{P}, p \mid x - y, p \perp xy\)：

• \(n \perp p\)：\(\nu_p(x^n - y^n) = \nu_p(x - y)\)。

  证明：因式分解：\(x^n - y^n = (x - y) \sum \limits_{i = 0}^{n - 1} x^i y^{n - 1 - i}\)。

  因为 \(p \mid x - y \implies x \equiv y \pmod p\) 且 \(n \perp p\)，所以 \(\sum \limits_{i = 0}^{n - 1} x^i y^{n - 1 - i} \equiv nx^{n - 1} \not \equiv 0 \pmod p\)。

  故只有 \(x - y\) 对 \(x^n - y^n\) 产生贡献。证毕。

• \(p^2 \mid x - y\) 或 \(p \neq 2\)：\(\nu_p(x^n - y^n) = \nu_p(x - y) + \nu_p(n)\)。

证明：设 \(\alpha = \nu_p(x - y), n = p^{\beta} \gamma\)，则 \(p^{\alpha} \mid x - y \implies \exist q \perp p, x = p^{\alpha} q + y\)。

则：

\[\begin{aligned} x^n - y^n &= (p^{\alpha} q + y)^n - y^n \\ &= y^n + \binom{n}{1} p^{\alpha} qy^{n - 1} + \binom{n}{2} p^{2 \alpha} q^2 y^{n - 2} + \cdots + p^{n \alpha} q^n - y^n \\ &= \binom{n}{1} p^{\alpha} qy^{n - 1} + \binom{n}{2} p^{2 \alpha} q^2 y^{n - 2} + \cdots + p^{n \alpha} q^n \end{aligned} \]

设 \(f(i) = \dbinom{n}{i} p^{i \alpha} q^i y^{n - i}\)。

分类讨论：（想证明第一项有最少的 \(p\)，但难度过大，于是尝试加强条件，以分类讨论的方式叙述。）

• \(\beta = 1\)：容易发现，\(f(1) = \alpha + 1\)。
  • \(\alpha = 1, p = 2\)：\(f(2) = 2 \alpha = \alpha + 1 = f(1)\)。
  • 否则：\(f(1) < f(2) < f(3) < \cdots < f(n)\)，此时 \(\nu_p(x^n - y^n) = \alpha + 1 = \nu_p(x - y) + 1\)。

······

0x05. 不定方程

1.（Bezout 定理）不定方程 \(ax + by = \gcd(a, b)\) 一定有解。

2. 对于不定方程 \(ax + by = c\)，若 \((x_0, y_0)\) 为一组解且 \(d = \gcd(a, b)\)，则方程的所有解均为 \((x, y) = \left( x_0 + \dfrac{bt}{d}, y_0 - \dfrac{at}{d} \right) \quad (t \in \mathbb{Z})\)。

证明：代入可知，\(\left( x_0 + \dfrac{bt}{d}, y_0 - \dfrac{at}{d} \right)\) 为一组解。下证所有解都是这个形式。

考虑另一组解 \((x_1, y_1)\)，可得 \(a(x_1 - x_0) + b(y_1 - y_0) = 0 \implies a(x_1 - x_0) = b(y_0 - y_1)\)。

设 \(d = \gcd(a, b), a = da', b = db'\)，则 \(a'(x_1 - x_0) = b'(y_0 - y_1)\)。

······

3.（Frobenius 问题）给定正整数 \(a, b, c\) 满足 \(a \perp b\)。对于不定方程 \(ax + by = c\)，有：

• \(c > (a - 1)(b - 1) + 1 = ab - a - b\) 时，方程必有非负整数解。

• \(c = (a - 1)(b - 1) + 1 = ab - a - b\) 时，方程没有非负整数解。

  证明：容易发现，\((x, y) = (b - 1, -1)\) 为一组整数解，则 \((x, y) = ((b - 1) + bt, -1 - at)\) 也为一组解。

  因为 \((b - 1) + bt \ge 0\)，所以 \(t \ge 0\)。

  因为 \(-1 - at \ge 0\)，所以 \(t < 0\)。

  两者无交集，故无非负整数解。证毕。

• \(c < (a - 1)(b - 1) + 1 = ab - a - b\) 时，共有 \(\left \lfloor \dfrac{(a - 1)(b - 1)}{2} \right \rfloor\) 个 \(c\) 可以让方程有解。

0x06. 同余

1.（同余的性质）

• （自反性）\(a \equiv a \pmod m\)。
• （对称性）\(a \equiv b \pmod m \implies b \equiv a \pmod m\)。
• （传递性）\(a \equiv b \pmod m, b \equiv c \pmod m \implies a \equiv c \pmod m\)。
• \(a \equiv b \pmod m, c \equiv d \pmod m \implies a \pm c \equiv b \pm d \pmod m\)。
• \(a \equiv b \pmod m, c \equiv d \pmod m \implies ac \equiv bd \pmod m\)。
• \(a \equiv b \pmod m \implies ak \equiv bk \pmod{mk}\)。
• \(a \equiv b \pmod m, d \mid m \implies a \equiv b \pmod d\)。
• \(a \equiv b \pmod m, d \mid a, d \mid b \implies \dfrac{a}{d} \equiv \dfrac{b}{d} \pmod{\dfrac{m}{\gcd(d, m)}}\)。

2. 若 \(n \perp m\)，\(a_0, a_1, \cdots, a_{m - 1}\) 是模 \(m\) 意义下的一个完全剩余系，则对于任意整数 \(b\)，\(a_0 n + b, a_1 n + b, \cdots, a_{m - 1} n + b\) 也是模 \(m\) 意义下的一个完全剩余系。

证明：注意到，\(+b\) 操作没有任何影响，故我们忽略它。下证 \(a_0 n, a_1 n, \cdots, a_{m - 1} n\) 是模 \(m\) 的完系。

我们只需证明，\(a_0 n, a_1 n, \cdots, a_{m - 1} n\) 在模 \(m\) 意义下无重复即可。

我们假设存在 \(i, j\) 满足 \(i \neq j, a_i n \equiv a_j n \pmod m\)。

因为 \(n \perp m\)，所以 \(a_i \equiv a_j \pmod m\)。

又因为 \(a\) 为完系，所以 \(i = j\)，与假设矛盾！

故 \(a_0 n, a_1 n, \cdots, a_{m - 1} n\) 是模 \(m\) 的完系，证毕。

3. 对于模 \(m\) 的剩余类 \(S_i\)，\(\forall x, y \in S_i, \gcd(x, m) = \gcd(y, m)\)。

证明：设 \(y = x + km\)，则 \(\gcd(y, m) = \gcd(x + km, m) = \gcd(x, m)\)。

4. 对于模 \(m\) 的缩系 \(a_0, a_1, \cdots a_{\varphi(m)}\) 和 \(k \perp m\)，\(ka_0, ka_1, \cdots ka_{\varphi(m)}\) 也是缩系。

证明：对于任意的 \(0 \le i \le \varphi(m)\)，有 \(a_i \perp m, k \perp m\)，故 \(ka_i \perp m\)。

又容易发现，\(ka_0, ka_1, \cdots ka_{\varphi(m)}\) 两两不同。证毕。

5.（逆元的性质）

• \((a^{-1})^{-1} \equiv a \pmod m\)。
• \((ab)^{-1} \equiv a^{-1} b^{-1} \pmod m\)。
• \(\dfrac{1}{a} + \dfrac{1}{b} \equiv \dfrac{a + b}{ab} \pmod m\)。

6. 设 \(f(x)\) 为整系数多项式，则 \(\forall m \in \mathbb{N}^+, n \equiv n' \pmod m \implies f(n) \equiv f(n') \pmod m\)。

7.（Euler 定理）对于 \(a \perp m\)，\(a^{\varphi(m)} \equiv 1 \pmod m\)。

证明：考虑模 \(m\) 的缩系 \(\{ b_i \}\)，则 \(b_1 b_2 \cdots b_{\varphi(m)} \equiv (ab_1) (ab_2) \cdots (ab_{\varphi(m)}) = a^{\varphi(m)} b_1 b_2 \cdots b_{\varphi(m)} \pmod m\)。

因为 \(b_1 b_2 \cdots b_{\varphi(m)} \perp m\)，所以 \(a^{\varphi(m)} \equiv 1 \pmod m\)。证毕。

7.1.（费马小定理）对于 \(p \in \mathbb{P}\)，\(a^{p - 1} \equiv 1 \pmod p\)。

证明：因为 \(p \in \mathbb{P}\)，所以 \(\varphi(p) = p - 1\)，所以 \(a^{\varphi(p)} = a^{p - 1} \equiv 1 \pmod p\)。证毕。

8.（Wilson 定理）对于 \(p \in \mathbb{P}\)，有 \((p - 1)! \equiv -1 \pmod p\)。

9. 对于完全对称（指数、系数都对称）的 \(\varphi(m)\) 元整系数多项式 \(f(x_1, x_2, \cdots, x_{\varphi(m)})\)，和两个模 \(m\) 的缩系 \(\{ a_i \}, \{ b_i \}\)，有：

\[f(a_1, a_2, \cdots, a_{\varphi(m)}) \equiv f(b_1, b_2, \cdots, b_{\varphi(m)}) \pmod m \]

评注：做题时常用 \(f(x_1, x_2, \cdots, x_{\varphi(m)})\) 为 \(\sum x_i\)、\(\prod x_i\)、\(\sum x_i^k\) 进行分析。

10.（Lucas 定理）对于 \(n, m \in \mathbb{N}, p \in \mathbb{P}\)，有 \(\dbinom{n}{m} \equiv \dbinom{\lfloor n / p \rfloor}{\lfloor m / p \rfloor} \dbinom{n \bmod p}{m \bmod p} \pmod p\)。

证明：我们发现：

\[\begin{aligned} (1 + p)^n &= \sum_{i = 0}^n \dbinom{n}{i} p^i \\ &= 1 + p^n + \sum_{i = 1}^{n - 1} \dbinom{n}{i} p^i \\ &\equiv 1 + p^n \end{aligned} \pmod p \]

则：

\[\begin{aligned} \dbinom{n}{m} &\equiv [x^m] (1 + x)^n \\ &\equiv [x^m] \big( (1 + x)^{p \lfloor n / p \rfloor} (1 + x)^{n \bmod p} \big) \\ &\equiv [x^m] \big( (1 + x^p)^{\lfloor n / p \rfloor} (1 + x)^{n \bmod p} \big) \\ &\equiv [x^{m \bmod p}] (1 + x)^{n \bmod p} \cdot [x^{\lfloor m / p \rfloor}] (1 + x^p)^{\lfloor n / p \rfloor} \\ &\equiv \dbinom{n \bmod p}{m \bmod p} \dbinom{\lfloor n / p \rfloor}{\lfloor m / p \rfloor} \end{aligned} \pmod p \]

证毕。

11. 同余方程 \(ax \equiv b \pmod m\) 有解的充要条件为 \(\gcd(a, m) \mid b\)。

证明：\(ax \equiv b \pmod m\) 等价于 \(m \mid ax - b\)。

设 \(y = \dfrac{ax - b}{m}\)，则原方程等价于 \(ax - my = b\)。

根据裴蜀定理，该方程仅在 \(\gcd(a, m) \mid b\) 时有解。证毕。

12.（中国剩余定理）设 \(m_1, m_2, \cdots, m_k \in \mathbb{N}^+\) 两两互素，则对于任意 \(b_1, b_2, \cdots, b_k \in \mathbb{Z}\)，同余方程组：

\[\begin{cases} x \equiv b_1 \pmod{m_1} \\ x \equiv b_2 \pmod{m_2} \\ \cdots \\ x \equiv b_k \pmod{m_k} \end{cases} \]

必有解，且解在模 \(\prod \limits_{i = 1}^k m_i\) 意义下唯一。

存在性的证明（归纳法）：首先证明 \(k = 2\) 时必有解。

设 \(x_0 = km_1 + b_1\)，则只需证存在 \(k\)，使得 \(x_0 = km_1 + b_1\) 满足 \(x_0 \equiv b_2 \pmod{m_2}\)。

不妨令 \(0 \le k < m_2\)，则所有的 \(k\)（\(K = \{ 0, 1, \cdots, m_2 - 1 \}\)）构成模 \(m_2\) 的完系，故 \(X = \{ b_1, m_1 + b_1, 2m_1 + b_1 \cdots, (m_2 - 1)m_1 + b_1 \}\) 构成模 \(m_2\) 的完系（因为 \(m_1 \perp m_2\)），故 \(b_2 \in X\)，则 \(k = 2\) 时必有解。

现设 \(k = k_0\) 时有解，下证 \(k = k_0 + 1\) 时有解。

设 \(k = k_0\) 时的解为 \(x_0\)，则可得方程组：

\[\begin{cases} x \equiv b \pmod{\prod \limits_{i = 1}^{k_0} m_i} \\ x \equiv b_{k_0 + 1} \pmod{m_{k_0 + 1}} \end{cases} \]

注意到，\(m_{k_0 + 1} \perp \prod \limits_{i = 1}^{k_0} m_i\)，故上述方程组有解。证毕。

唯一性的证明：假设原方程组在模 \(\prod \limits_{i = 1}^k m_i\) 意义下有解 \(x_1, x_2\) 满足 \(x_1 \not \equiv x_2 \pmod{\prod \limits_{i = 1}^k m_i}\)。

则 \(x_1 \equiv b_1 \pmod{m_1}\) 且 \(x_2 \equiv b_1 \pmod{m_1}\)。

两式相减得 \(x_1 - x_2 \equiv 0 \pmod{m_1} \implies x_1 \equiv x_2 \pmod{m_1} \implies m_1 \mid x_1 - x_2\)。同理可得 \(\forall i, m_i \mid x_1 - x_2\)。

因为 \(m_1, m_2, \cdots, m_k\) 两两互素，所以 \(\prod \limits_{i = 1}^{k_0} m_i \mid x_1 - x_2 \implies x_1 \equiv x_2 \pmod{\prod \limits_{i = 1}^k m_i}\)，与假设矛盾！证毕。

13. 同余方程组：

\[\begin{cases} a_1 x \equiv b_1 \pmod{m_1} \\ a_2 x \equiv b_2 \pmod{m_2} \end{cases} \]

有解的充分条件为：\(\gcd(a_1, m_1) \mid b_1, \gcd(a_2, m_2) \mid b_2, m_1 \perp m_2\)。

14. \(a\) 模 \(m\) 的阶 \(k\) 满足 \(k \mid \varphi(m)\)。

证明：\(k\) 为数列 \(b_i = a^i\) 的最小正周期，而 \(\varphi(m)\) 也为该数列的最小正周期，故 \(k \mid \varphi(m)\)。证毕。

15. 对于 \(a^m \equiv a^n \pmod p\)，设 \(k\) 为 \(a\) 模 \(p\) 的阶，则 \(m \equiv n \pmod k\)。

证明：设 \(m = q_1 k + r_1, n = q_2 k + r_2\) 满足 \(0 \le r_1, r_2 < k\)。

则 \(a^{q_1 k} \cdot a^{r_1} \equiv a^{q_2 k} \cdot a^{r_2} \pmod p \implies (a^{k})^{q_1} \cdot a^{r_1} \equiv (a^{k})^{q_2} \cdot a^{r_2} \pmod p\)。

因为 \(k\) 为 \(a\) 模 \(p\) 的阶，所以 \(a^k \equiv 1 \pmod p\)，所以 \(\forall i, (a^k)^i \equiv 1 \pmod p\)。

则 \(a^{r_1} \equiv a^{r_2} \pmod p\)。

又因为 \(r_1, r_2 < k\)，所以 \(r_1 = r_2\)。证毕。

0x07. 进制

1.（进制数）对于非负整数 \(n, l\) 满足 \(l \ge 2\)，存在唯一 \(a_0, a_1, \cdots, a_k\) 满足 \(\forall i, 0 \le a_i < l, a_k > 0\)，且 \(n = \sum \limits_{i = 0}^k a_i \cdot l^i\)。

存在性的证明（归纳法）：容易发现，\(n \in [0, l - 1]\) 时只需令 \(a_0 = n\) 即可。

作归纳假设：原命题对于 \(n \in [0, l^i - 1]\) 成立。下证该命题对 \(n \in [l^i, l^{i + 1} - 1]\) 成立。

作带余除法，设 \(n = q \cdot l^i + r\)，则 \(r \in [0, l^i - 1]\)。

根据归纳假设，设 \(r = \sum \limits_{j = 0}^{i - 1} b_j \cdot l^j\)，则 \(a_j = [j < i] \cdot b_j + [j = i] \cdot q\) 即为合法构造。证毕。

唯一性的证明：注意到：（技巧：如此形式的恒等式在进制数问题上比较有用。）

\[l^i = 1 + \sum_{j < i} (i - 1) \cdot l^j = 1 + (i - 1) \sum_{j < i} l^j \tag{1} \]

假设存在 \(n = \sum \limits_{i = 0}^k a_i \cdot l^i = \sum \limits_{i = 0}^k b_i \cdot l^i\) 满足 \(\exist i, a_i \neq b_i\)。

设 \(c_i = a_i - b_i\)，则 \(0 = \sum \limits_{i = 0}^k c_i \cdot l_i\)。

若存在 \(c_i > 0\)，设 \(i'\) 为最大的 \(i\) 满足该条件。则根据 \((1)\) 式，无论如何，\(\sum \limits_{i = 0}^k c_i \cdot l_i > 0\)，矛盾！故不存在 \(c_i > 0\)。同理，不存在 \(c_i < 0\)。

故 \(\forall i, c_i = 0 \implies \forall i, a_i = b_i\)，与假设矛盾！证毕。

0x08. 冷门结论 & 定理

1.（Beatty 定理）对正无理数 \(\alpha, \beta\) 满足 \(\dfrac{1}{\alpha} + \dfrac{1}{\beta} = 1\)，设集合 \(S = \{ \lfloor \alpha \rfloor, \lfloor 2 \alpha \rfloor, \lfloor 3 \alpha \rfloor, \cdots \}, T = \{ \lfloor \beta \rfloor, \lfloor 2 \beta \rfloor, \lfloor 3 \beta \rfloor, \cdots \}\)，则 \(S, T\) 划分 \(\mathbb{N}^+\)。

2.（Hermite 恒等式）

\[\lfloor x \rfloor + \left \lfloor x + \dfrac{1}{n} \right \rfloor + \left \lfloor x + \dfrac{2}{n} \right \rfloor + \cdots + \left \lfloor x + \dfrac{n - 1}{n} \right \rfloor = \lfloor nx \rfloor \quad (n \in \mathbb{N}^+) \]

3. 若质数 \(q \mid M_p\)（其中 \(M_p\) 为梅森数），则 \(p \mid q - 1\)。

4. 设费马数 \(F_n\) 的质因子为 \(p\)，则 \(2^{n + 1} \mid p - 1\)。

组合数学篇

0x01. 定义

1. 下降幂：\(n^{\underline{k}} = \prod \limits_{i = 0}^{k - 1} (n - i)\)。

2. 组合数：

\[\binom{n}{k} = \begin{cases} \dfrac{n^{\underline{k}}}{k!}, &k \ge 0 \\ 0 &k < 0 \end{cases} \quad ({\color{red} n \in \mathbb{R}}, k \in \mathbb{N}) \]

0x02. 定理 & 结论

1.（常用恒等式）

• （吸收 / 提取恒等式）\(\dbinom{n}{k} = \dfrac{n}{k} \dbinom{n - 1}{k - 1}\)。

  证明：先移项：\(k \dbinom{n}{k} = n \dbinom{n - 1}{k - 1}\)。

  此时，\(\mathrm{LHS}\) 表示如下过程的方案数：先在 \(n\) 个人中选 \(k\) 个人，再在这 \(k\) 个人中选 1 个组长。

  而 \(\text{RHS}\) 表示如下过程的方案数：先在 \(n\) 个人中选 1 个组长，后在 \(n - 1\) 个人中选 \(k - 1\) 个人。

  这两种方式选出的组的方案完全相同，证毕。

• （对称恒等式）\(\dbinom{n}{k} = \dbinom{n}{n - k}\)。

• （杨辉三角）\(\dbinom{n}{k} = \dbinom{n - 1}{k - 1} + \dbinom{n - 1}{k}\)。

• （相伴恒等式）\((n - k) \dbinom{n}{k} = n \dbinom{n - 1}{k}\)。

  证明：\(\mathrm{LHS}\) 表示在 \(n\) 个人选 \(k\) 人当组员，再在剩下 \(n - k\) 人中选组长的方案数。

  \(\text{RHS}\) 表示在 \(n\) 个人中选 \(1\) 人当组长，再在剩下 \(n - 1\) 人中选 \(k\) 人当组员的方案数。

  故两者等价，证毕。

• （三项系数恒等式）\(\dbinom{n}{m} \dbinom{m}{k} = \dbinom{n}{k} \dbinom{n - k}{m - k}\)。

  证明 1：

  \[\begin{aligned} \dbinom{n}{m} \dbinom{m}{k} &= \dfrac{n!}{m! (n - m)!} \cdot \dfrac{m!}{k! (m - k)!} \\ &= \dfrac{n!}{k! (n - m)! (m - k)!} \\ &= \dfrac{n! (n - k)!}{k! (n - m)! (m - k)! (n - k)!} \\ &= \dfrac{n!}{k! (n - k)!} \cdot \dfrac{(n - k)!}{(m - k)! (n - m)!} \\ &= \dfrac{n!}{k! (n - k)!} \cdot \dfrac{(n - k)!}{(m - k)! ((n - k) - (m - k))!} \\ &= \dbinom{n}{k} \dbinom{n - k}{m - k} \end{aligned} \]

  证毕。

  证明 2（组合意义）：\(\mathrm{LHS}\) 表示在 \(n\) 个红球中选 \(m\) 个染白，再在这 \(m\) 个白球中选 \(k\) 个染黑的方案数。

  \(\mathrm{RHS}\) 表示在 \(n\) 个红球中选 \(k\) 个染黑，再在剩余 \(n - k\) 个红球中选 \(m - k\) 个染白的方案数。

  显然，这两个过程等价，故方案数相等。证毕。

• （上指标求和）\(\sum \limits_{i = k}^n \dbinom{i}{k} = \dbinom{n + 1}{k + 1}\)。

  证明（组合意义）：\(\mathrm{LHS}\) 表示钦定选择的最后一个物品前有 \(i\) 个物品（共有 \(n + 1\) 个物品），除最后一个物品外还要再选择 \(k\) 个物品的方案数。

  \(\mathrm{RHS}\) 表示在 \(n + 1\) 个物品中选 \(k + 1\) 个物品的方案数。

  注意到，这两个过程等价，故方案数相等。证毕。

• （Vandermorde 恒等式）\(\sum \limits_k \dbinom{a}{m + k} \dbinom{b}{n - k} = \dbinom{a + b}{m + n}\)。

• （上指标卷积）\(\sum \limits_{i = 0}^n \dbinom{i}{a} \dbinom{n - i}{b} = \dbinom{n + 1}{a + b + 1}\)。

• （上指标反转）\(\dbinom{n}{k} = (-1)^k \dbinom{k - n - 1}{k}\)。

• \(n! = \sum \limits_{i = 0}^n (-1)^i \dbinom{n}{i} (n - i)^n\)。

• \(\sum \limits_{i = 0}^n \dbinom{n - i}{i} = F_{n + 1}\)，其中 \(F\) 为 Fibonacci 数列。

• \(\dbinom{n + k}{k}^2 = \sum \limits_{j = 0}^k \dbinom{k}{j}^2 \dbinom{n + 2k - j}{2k}\)。

2.（多重集划分）给定 \(n\) 个元素和长度为 \(k\) 的数列 \(m\) 满足 \(\sum \limits_{i = 1}^k m_i = n\)，对于所有 \(1 \le i \le k\)，将这 \(n\) 个元素选 \(m_i\) 个放入多重集 \(A_i\) 中，则有 \(\dfrac{n!}{\prod m_i!}\) 种方案数。

证明：可以发现，方案数为：

\[\prod_{i = 1}^k \dbinom{n - \sum \limits_{1 \le j < i} m_j}{m_i} \]

代入组合数的定义后化简即证。

3.1.（圆排列）将 \(n\) 个元素不分首尾排成一圈的方案有 \((n - 1)!\) 种。

证明：若不排成一圈，则有 \(n!\) 种。注意到每种圆排列被重复算了 \(n\) 次，故除以 \(n\) 得 \((n - 1)!\) 种，证毕。

3.2. 在 \(n\) 个元素中选 \(k\) 个元素不分首尾排成一圈的方案有 \(\dfrac{1}{k} \dbinom{n}{k}\) 种。

4.1. 不定方程 \(\sum \limits_{i = 1}^k x_i = n\) 的正整数解有 \(\dbinom{n - 1}{k - 1}\) 种。

证明（插板法）：注意到每一组解都对应着一种把 \(n\) 个 \(1\) 分组的方法。如在 \(n = 10, k = 3\) 时，\((x_1, x_2, x_3) = (3, 3, 4)\) 等价于：

\[\underbrace{1 \ 1 \ 1}_{x_1} \mid \underbrace{1 \ 1 \ 1}_{x_2} \mid \underbrace{1 \ 1 \ 1 \ 1}_{x_3} \]

故原问题等价于：在 \(n\) 个 \(1\) 形成的 \(n - 1\) 的空隙中插入 \(k - 1\) 个板的方案数。

容易发现答案为 \(\dbinom{n - 1}{k - 1}\)，证毕。

4.2. 不定方程 \(\sum \limits_{i = 1}^k x_i = n\) 且 \(\forall i, x_i \ge a_i\) 的解有 \(\dbinom{n + k - \sum a_i - 1}{k - 1}\) 种。

证明：考虑将 \(x_i\) 减掉 \(a_i - 1\)，问题就变成了 4.1，则有 \(\dbinom{n - 1 - \sum \limits_{i = 1}^k (a_i - 1)}{k - 1} = \dbinom{n + k - \sum a_i - 1}{k - 1}\) 种，证毕。

4.3. 不等式 \(\sum \limits_{i = 1}^k x_i < n\) 的正整数解有 \(\dbinom{n - 1}{k}\) 种。

证明：考虑令 \(x_{k + 1} = n - \sum \limits_{i = 1}^k x_i\)，问题就变成了 4.1，则有 \(\dbinom{n - 1}{k}\) 种，证毕。

5. 见此。模板题为 P5824 十二重计数法。

6.（二项式反演）设 \(g_n = \sum \limits_{i = 0}^n \dbinom{n}{i} f_i\)，则 \(f_n = \sum \limits_{i = 0}^n \dbinom{n}{i} (-1)^i g_{n - i}\)。

证明（生成函数）：设 \(f, g\) 的 EGF 分别为 \(F(x), G(x)\)，数列 \((1, 1, 1, \cdots)\) 的 EGF 为：

\[1(x) = \sum \limits_{n \ge 0} \dfrac{x^n}{n!} = e^x \]

（技巧：见到组合数想 EGF。）

注意到 \(G(x) = F(x) \cdot 1(x) = e^x F(x)\)，则：

\[\begin{aligned} F(x) &= e^{-x} G(x) \\ &= \left( \sum_{n \ge 0} \dfrac{(-x)^n}{n!} \right) \left( \sum_{n \ge 0} g_n \dfrac{x^n}{n!} \right) \\ &= \left( \sum_{n \ge 0} (-1)^n \dfrac{x^n}{n!} \right) \left( \sum_{n \ge 0} g_n \dfrac{x^n}{n!} \right) \\ &= \sum_{n \ge 0} \left( \sum_{i = 0}^n \dbinom{n}{i} (-1)^i g_{n - i} \right) \dfrac{x^n}{n!} \end{aligned} \]

则：

\[f_n = \sum_{i = 0}^n \dbinom{n}{i} (-1)^i g_{n - i} \]

证毕。

7.（抽屉原理）将 \(n\) 个物品分成 \(k\) 组，则存在至少一组有 \(\ge \left \lceil \dfrac{n}{k} \right \rceil\) 个物品。

评注：常用 \(k = n - 1\)。

8.（Fibonacci 数列的性质）设 \(F\) 为 Fibonacci 数列，则有：

• \(F_n = \dfrac{\left( \frac{1 + \sqrt{5}}{2} \right)^n - \left( \frac{1 - \sqrt{5}}{2} \right)^n}{\sqrt{5}}\)。

• 设：

  \[P = \begin{bmatrix} 0 & 1 \\ 1 & 1 \end{bmatrix} \]

  则：

  \[\begin{bmatrix} F_{n - 1} & F_n \end{bmatrix} = \begin{bmatrix} F_{n - 2} & F_{n - 1} \end{bmatrix} P = \begin{bmatrix} F_0 & F_1 \end{bmatrix} P^n \]

• \(F_{2n} = F_n (2F_{n + 1} - F_n), F_{2n + 1} = F_n^2 + F_{n + 1}^2\)。

• （Cassini 恒等式）\(F_{n - 1} F_{n + 1} - F_n^2 = (-1)^n\)。

• （附加性质）\(F_{n + k} = F_{n} F_{k + 1} + F_{k - 1} F_n\)。

  • 特例：\(F_{2n} = F_n (F_{n + 1} + F_{n - 1})\)。

• \(a \mid b \iff F_a \mid F_b\)。

• \(\gcd(F_a, F_b) = F_{\gcd(a, b)}\)。

几何篇

0x00. 定义 & 概念

1. 命题：在一定范围内可以用语言、符号或式子表达的，可以判断真假的陈述句叫命题，其一般形式为“若 \(P\)，那么 \(Q\)”，即 \(P \implies Q\)。

2. 逆命题：一个命题的逆命题可以通过将条件与结论交换而得到。形式化的说，命题 \(P \implies Q\) 的逆命题为 \(Q \implies P\)。

3. 同一法：在证明一个命题时，先构造出同时符合条件与结论的情况，再说明这是唯一一种同时符合条件与结论的情况。

4. 圆幂：定义 \(\odot O\) 的圆幂为 \(p(E) = OE^2 - r^2\)，其中 \(r\) 为 \(\odot O\) 的半径。

5. 费马点：若在 \(\triangle ABC\) 内部的点 \(P\) 满足 \(AP + BP + CP\) 为最小值，则定义点 \(P\) 为 \(\triangle ABC\) 的费马点。

0x01. 一般三角形

1.（三角形全等的判定）判定两个三角形全等有 6 种方法：SAS^[1]、ASA、AAS、SSS、HL（SSA 的特例）、SSA（仅在等角的对边大于等角的邻边时可用）。

证明：SAS、ASA、HL 省略不证。对于剩下的，我们依次证明：

• AAS^[2]（反证法）：

  

  我们要证明 \(BC = EF\)。设：

  \[\begin{cases} \angle C = \angle F \\ \angle B = \angle E \\ AB = DE \end{cases} \]

  为导出矛盾，假设 \(BC > EF\)。选点 \(G\) 使得 \(BG = EF\)，连接 \(AG\)。此时可以发现：

  \[\begin{cases} AB = DE \\ \angle B = \angle E \\ BG = EF \end{cases} \]

  故 \(\triangle ABG \cong \triangle DEF\)，则 \(\angle AGB = \angle F\)。但是 \(\angle AGB > \angle C = \angle F\)，故矛盾，则 \(BC = EF\)。

  此时能够发现：

  \[\begin{cases} \angle B = \angle E \\ BC = EF \\ \angle C = \angle F \end{cases} \]

  故 \(\triangle ABC \cong \triangle DEF\)，原命题得证。

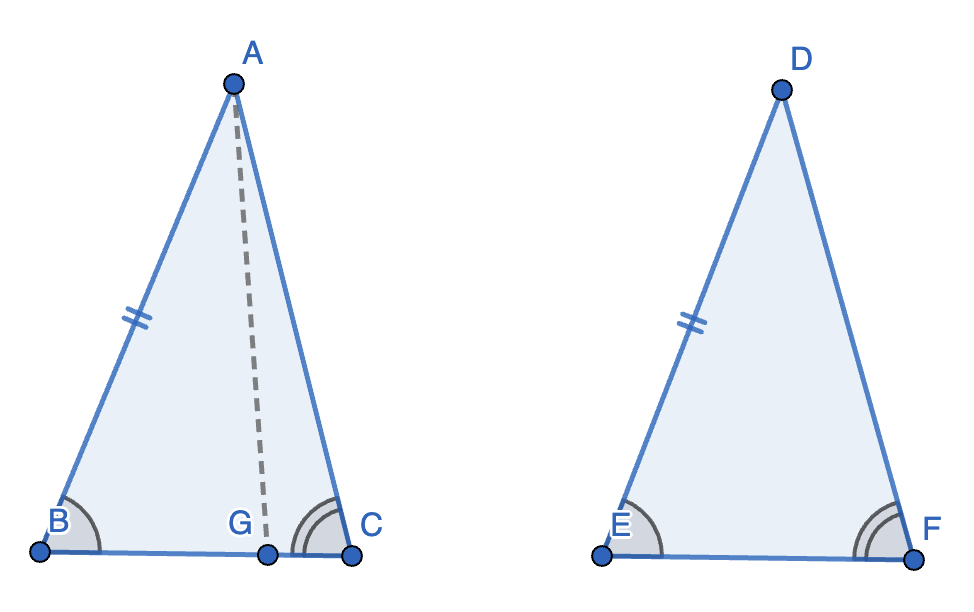
• SSS ^[3]：设两个三角形分别为 \(\triangle ABC\) 和 \(\triangle A'B'C'\)，且满足

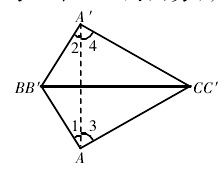
  \[\begin{cases} AB = A'B' \\ BC = B'C' \\ AC = A'C' \end{cases} \]

  将 \(\triangle ABC\) 经全等变换，使 \(BC\) 与 \(B'C'\) 重合，且 \(A\) 和 \(A'\) 分别在 \(BC\) 两侧。连接 \(AA'\)。

  

  因为 \(AB = A'B', AC = A'C'\)，所以 \(\angle 1 = \angle 2, \angle 3 = \angle 4\)，所以 \(\angle 1 + \angle 3 = \angle 2 + \angle 4\)，即 \(\angle A = \angle A'\)。

  此时可以发现：

  \[\begin{cases} AB = A'B' \\ \angle A = \angle A' \\ AC = A'C' \end{cases} \]

  故 \(\triangle ABC \cong \triangle A'B'C'\)，原命题得证。

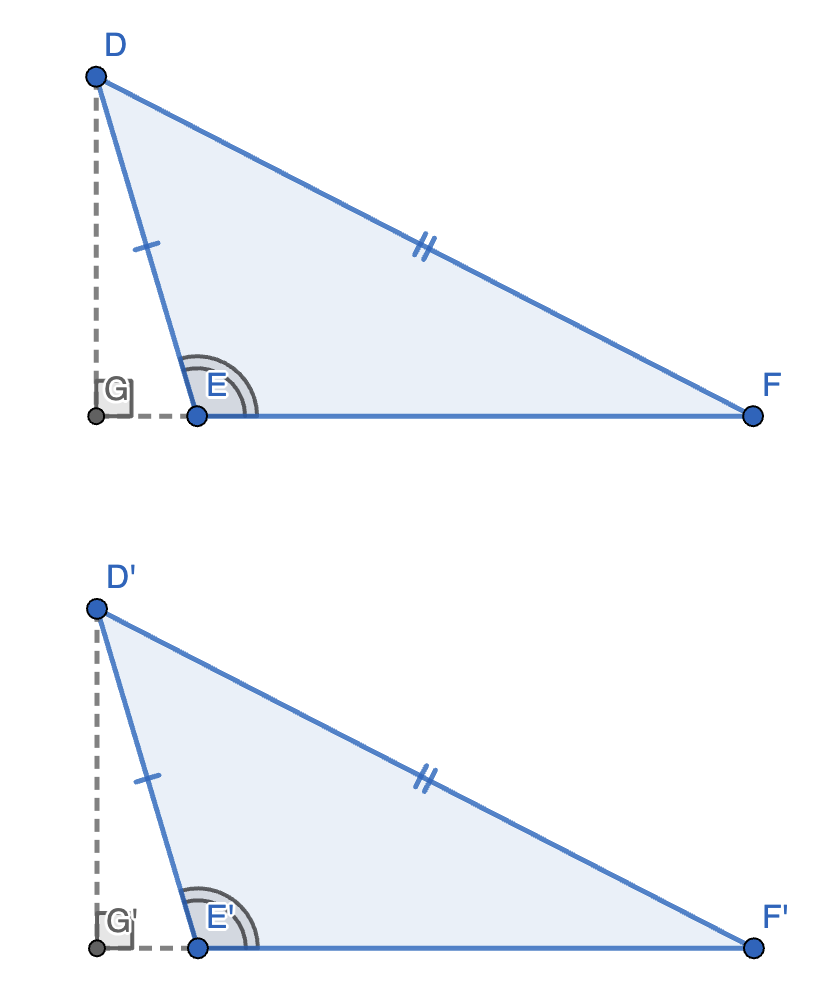
• SSA：我们先讨论其可用时的证明（第 1 部分），再讨论何时其不可用（第 2 部分）：

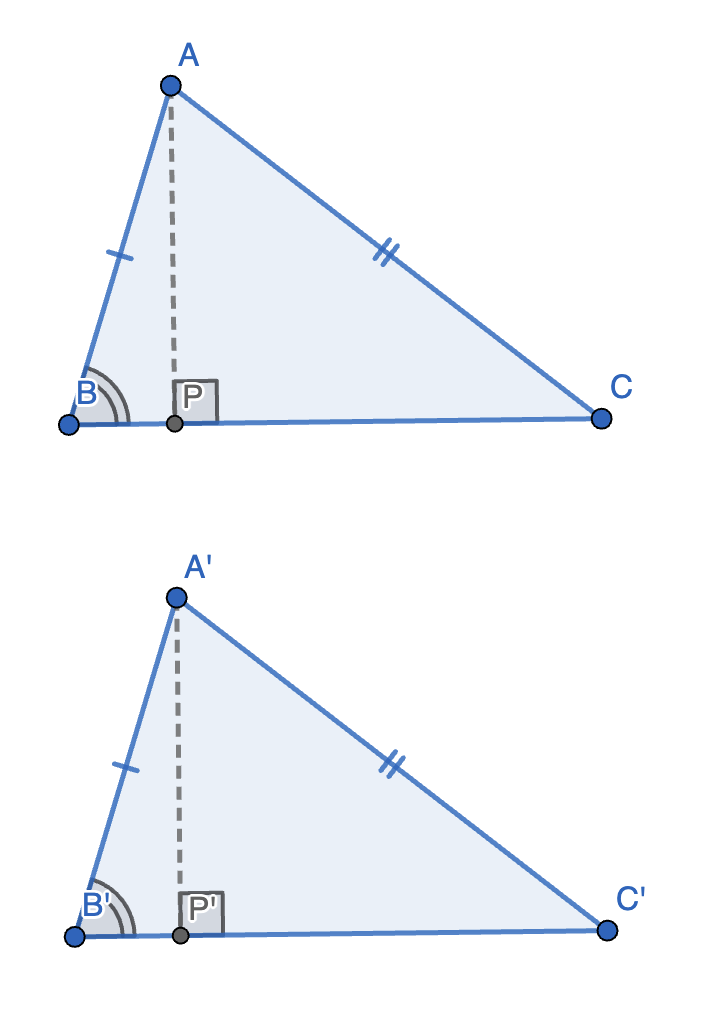
  • 第 1 部分：我们需要分类讨论其是否为钝角三角形：
  • 若不是：
    

  如图，已知：

  \[\begin{cases} \angle B = \angle B' \\ AB = A'B' \\ AC = A'C' \end{cases} \]

  作 \(\triangle ABC\) 在 \(BC\) 上的高交 \(BC\) 于点 \(P\)，以及 \(\triangle A‘B’C‘\) 在 \(B’C‘\) 上的高交 \(B‘C’\) 于点 \(P’\)。

  在 \(\triangle ABP\) 与 \(\triangle A'B'P'\) 中，

  \[\begin{cases} \angle APB = \angle A'P'B' = 90 \degree \\ \angle B = \angle B' \\ AB = A'B' \end{cases} \]

  故

  \[\triangle ABP \cong \triangle A'B'P' \tag{1} \]

  则 \(AP = A'P'\)。

  此时，在 \(\text{Rt} \triangle ACP\) 与 \(\text{Rt} \triangle A'C'P'\) 中，

  \[\begin{cases} AC = A'C' \\ AP = A'P' \end{cases} \]

  故

  \[\triangle ACP \cong \triangle A'C'P' \tag{2} \]

  由 \((1), (2)\) 知，\(\triangle ABC \cong \triangle A'B'C'\)。

  • 若是：
    

  如图，已知：

  \[\begin{cases} \angle E = \angle E' \\ DE = D'E' \\ DF = D'F' \end{cases} \]

  作 \(DG \perp EF\) 交 \(EF\) 于点 \(G\)，\(D'G' \perp E'F'\) 交 \(E'F'\) 于点 \(G'\)。

  因为 \(\angle E = \angle E'\)，所以 \(\angle DEG = \angle D'E'G'\)。

  在 \(\triangle DEG\) 与 \(\triangle D'E'G'\) 中，

  \[\begin{cases} \angle G = \angle G' \\ \angle DEG = \angle D'E'G' \\ DE = D'E' \end{cases} \]

  故

  \[\triangle DEG \cong \triangle D'E'G' \tag{1} \]

  则 \(DG = D'G'\)。

  此时，在 \(\text{Rt} \triangle DFG\) 与 \(\text{Rt} \triangle D'F'G'\) 中，

  \[\begin{cases} DG = D'G', \\ DF = D'F'。 \end{cases} \]

  故

  \[\triangle DFG \cong \triangle D'F'G' \tag{2} \]

  由 \((1), (2)\) 知，\(\triangle DEF \cong \triangle D'E'F'\)。

  故原命题得证。

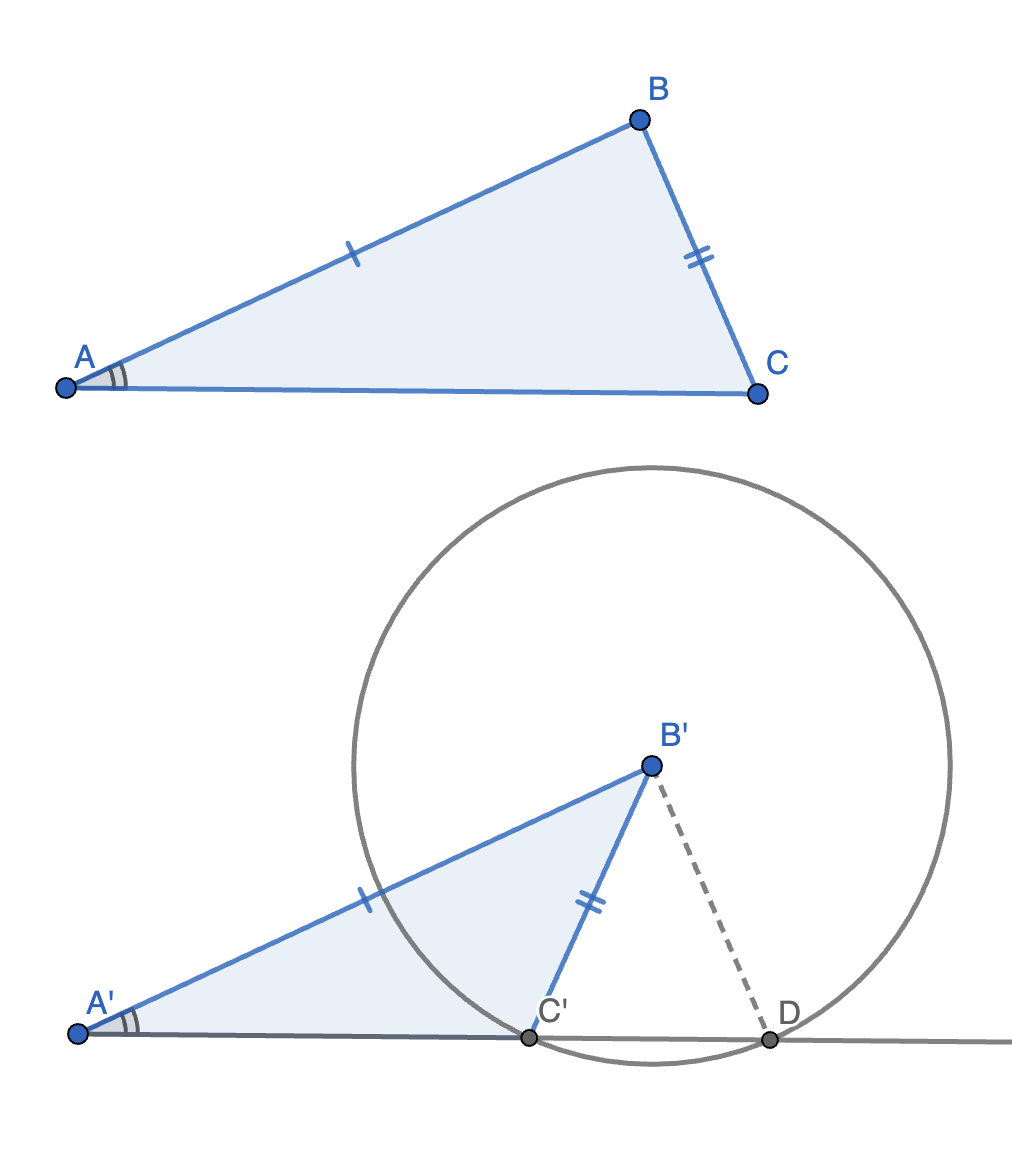
  • 第 2 部分：如图，已知
  \[\begin{cases} \angle A = \angle A' \\ AB = A'B' \\ BC = B'C' \end{cases} \]

  

  此时，按照 SSA 判定，两个三角形全等，但他们不全等。

  我们可以发现，原因为：图中的圆与射线 \(A'C'\) 有 2 个交点，故点 \(C'\) 的位置有 2 种可能，故不一定全等。

  于是，我们可以通过加长 \(BC\) 和 \(B'C'\)，使图中的圆与射线 \(A'C'\) 只有 1 个交点。此时满足 \(BC > AC, B'C' > A'C'\)。

证毕。

2.（共边定理）已知两个三角形 \(\triangle ABC, \triangle ABD\)，延长 \(AB\) 交 \(CD\) 于点 \(E\)，连接 \(CE, DE\). 设 \(S_{\triangle ABC} = S_1, S_{\triangle ABD} = S_2\)，则 \(\dfrac{S_1}{S_2} = \dfrac{CE}{DE}\).

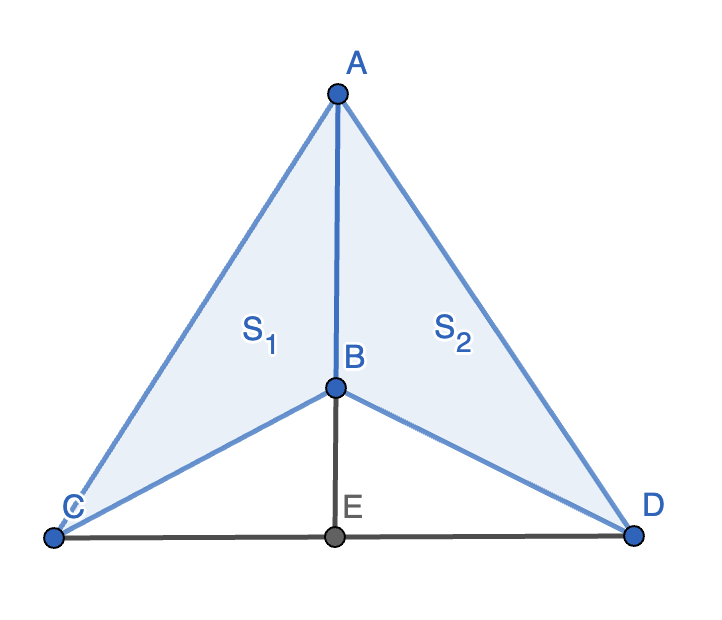
证明：容易发现，\(\dfrac{S_{\triangle ACE}}{S_{\triangle ADE}} = \dfrac{S_{\triangle BCE}}{S_{\triangle BDE}} = \dfrac{CE}{DE}\)，故 \(\dfrac{S_1}{S_2} = \dfrac{S_{\triangle ACE} - S_{\triangle BCE}}{S_{\triangle ADE} - S_{\triangle BDE}} = \dfrac{CE}{DE}\)。

故原命题得证。

3.（共角定理）已知 \(\triangle ABC\)，在 \(AB, AC\) 上分别任取一点 \(D, E\)，连接 \(DE\)。则 \(\dfrac{S_{\triangle ADE}}{S_{\triangle ABC}} = \dfrac{AD \cdot AE}{AB \cdot AC}\)。

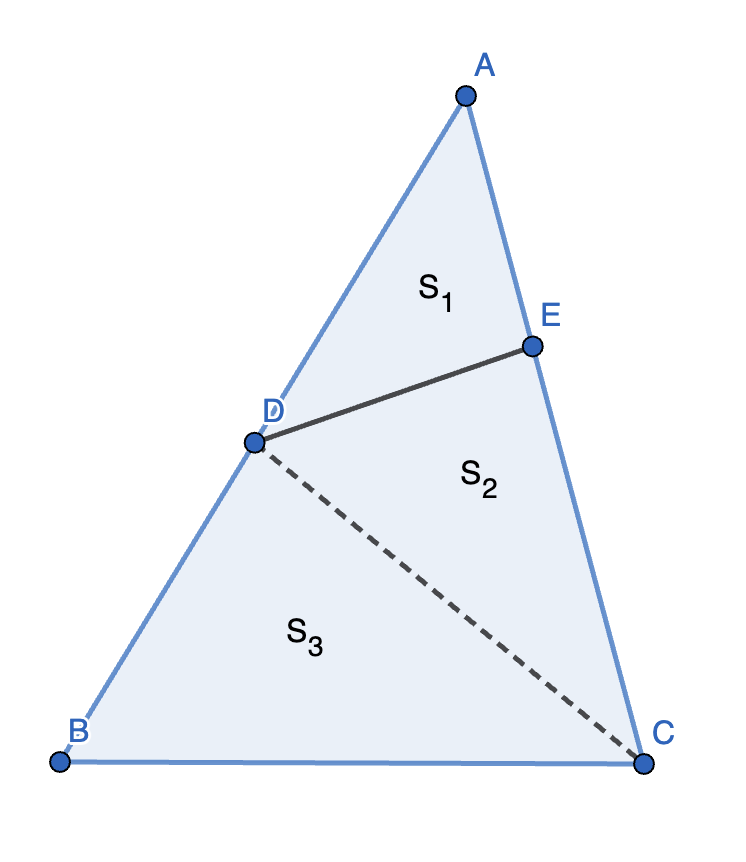
证明：连接 \(CD\)，设 \(S_1 = S_{\triangle ADE}, S_2 = S_{\triangle CDE}, S_3 = S_{\triangle BCD}, S = S_1 + S_2 + S_3\)。

则 \(\dfrac{S_1 + S_2}{S} = \dfrac{AD}{AB}, \dfrac{S_1}{S_1 + S_2} = \dfrac{AE}{AC}\)。

故 \(\dfrac{S_1}{S} = \dfrac{S_1 + S_2}{S} \cdot \dfrac{S_1}{S_1 + S_2} = \dfrac{AD}{AB} \cdot \dfrac{AE}{AC} = \dfrac{AD \cdot AE}{AB \cdot AC}\)。

故原命题得证。

4.（Ceva 定理）已知 \(\triangle ABC\)，在直线 \(AB, BC, CA\) 上分别任取一点 \(F, G, E\)，使得 \(AG, BE, CF\) 交于一点 \(D\)。则 \(\dfrac{AF}{FB} \cdot \dfrac{BG}{GC} \cdot \dfrac{CE}{EA} = 1\)。

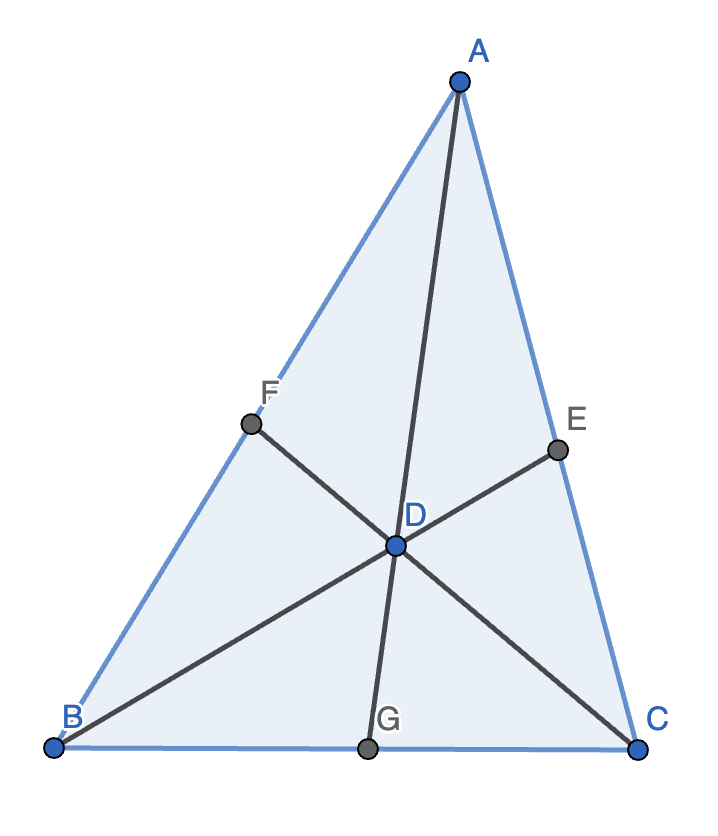
证明：如图，设 \(S_1 = S_{\triangle ACD}, S_2 = S_{\triangle BCD}, S_3 = S_{\triangle ABD}\)。

则 \(\dfrac{AF}{FB} = \dfrac{S_1}{S_2}, \dfrac{BG}{GC} = \dfrac{S_3}{S_1}, \dfrac{CE}{EA} = \dfrac{S_2}{S_3}\)。

故 \(\dfrac{AF}{FB} \cdot \dfrac{BG}{GC} \cdot \dfrac{CE}{EA} = \dfrac{S_1}{S_2} \cdot \dfrac{S_3}{S_1} \cdot \dfrac{S_2}{S_3} = 1\)。

在有点不在线段 \(AB, BC, AC\) 上的情形下，证明是类似的，证毕。

4.1.（Ceva 定理的逆定理）已知 \(\triangle ABC\)，在直线 \(AB, BC, CA\) 上分别任取一点 \(F, G, E\)，使得 \(\dfrac{AF}{FB} \cdot \dfrac{BG}{GC} \cdot \dfrac{CE}{EA} = 1\)。则 \(AG, BE, CF\) 交于同一点。

证明（同一法）：设 \(BE, CF\) 交于同一点 \(D\)，且 \(D\) 在 \(\triangle ABC\) 内，延长 \(AD\) 交 \(BC\) 于 \(G'\)。

此时可以发现：

\[\begin{cases} \frac{AF}{FB} \cdot \frac{BG}{GC} \cdot \frac{CE}{EA} = 1 \\ \frac{AF}{FB} \cdot \frac{BG'}{G'C} \cdot \frac{CE}{EA} = 1 \end{cases} \]

两式相除：

\[\dfrac{BG}{GC} = \dfrac{B'G}{G'C} \]

则：

\[\dfrac{BC - GC}{GC} = \dfrac{BC - G'C}{G'C} \]

于是：

\[\dfrac{BC}{GC} = \dfrac{BC}{G'C} \]

故 \(GC = G'C\)，\(G\) 与 \(G'\) 重合。

在有点不在线段 \(AB, BC, AC\) 上的情形下，证明是类似的，证毕。

4.2. 若 Ceva 定理成立，则在 \(E, F, G\) 中一定有偶数个点不在对应的线段上。

证明：我们引入有向线段，则 \(\dfrac{\overrightarrow{AF}}{\overrightarrow{FB}} \cdot \dfrac{\overrightarrow{BG}}{\overrightarrow{GC}} \cdot \dfrac{\overrightarrow{CE}}{\overrightarrow{EA}} = 1\)。

容易发现，对于三个点 \(A, B, C\)，若 \(\dfrac{\overrightarrow{AB}}{\overrightarrow{BC}} < 0\)，则 \(B\) 不在线段 \(AC\) 上。

因为 \(\dfrac{\overrightarrow{AF}}{\overrightarrow{FB}} \cdot \dfrac{\overrightarrow{BG}}{\overrightarrow{GC}} \cdot \dfrac{\overrightarrow{CE}}{\overrightarrow{EA}} > 0\)，则这三个分式中一定有偶数个负数，即在 \(E, F, G\) 中一定有偶数个点不在对应的线段上。

证毕。

5.（等差幂线定理）如图，已知 \(\triangle ABC\)，且 \(BE \perp AC\)，点 \(D\) 在直线 \(BE\) 上，连接 \(AD, CD\)。则 \(AB^2 - BC^2 = AD^2 - CD^2\)。

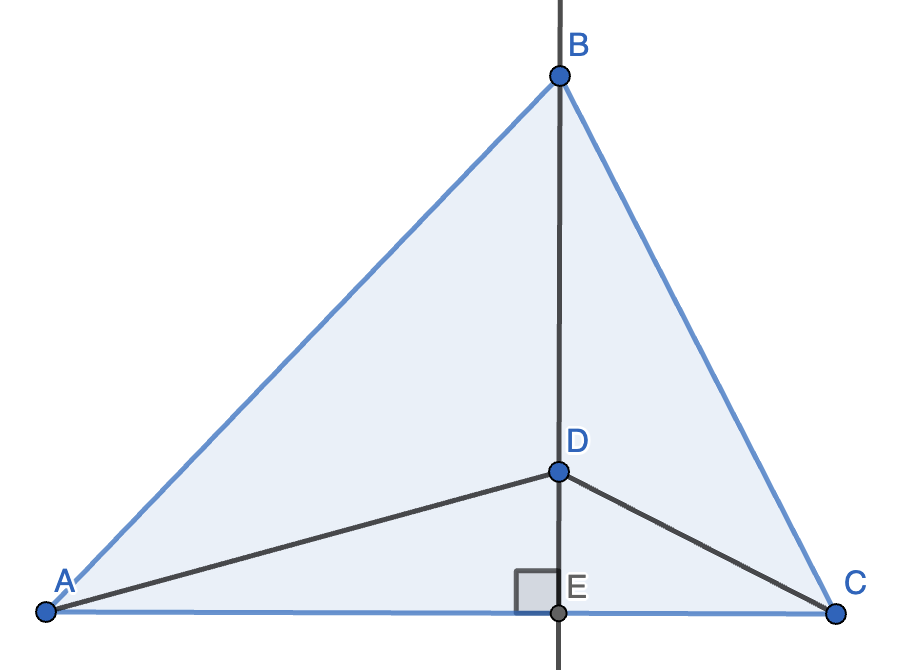
证明：根据勾股定理：

\[\begin{aligned} AB^2 = AE^2 + BE^2 \\ BC^2 = BE^2 + CE^2 \\ AD^2 = AE^2 + DE^2 \\ CD^2 = CE^2 + DE^2 \end{aligned} \]

则：

\[\begin{aligned} AB^2 - BC^2 &= AE^2 + BE^2 - BE^2 - CE^2 = AE^2 - CE^2 \\ AD^2 - CD^2 &= AE^2 + DE^2 - CE^2 - DE^2 = AE^2 - CE^2 \end{aligned} \]

故 \(AB^2 - BC^2 = AD^2 - CD^2\)，原命题成立。

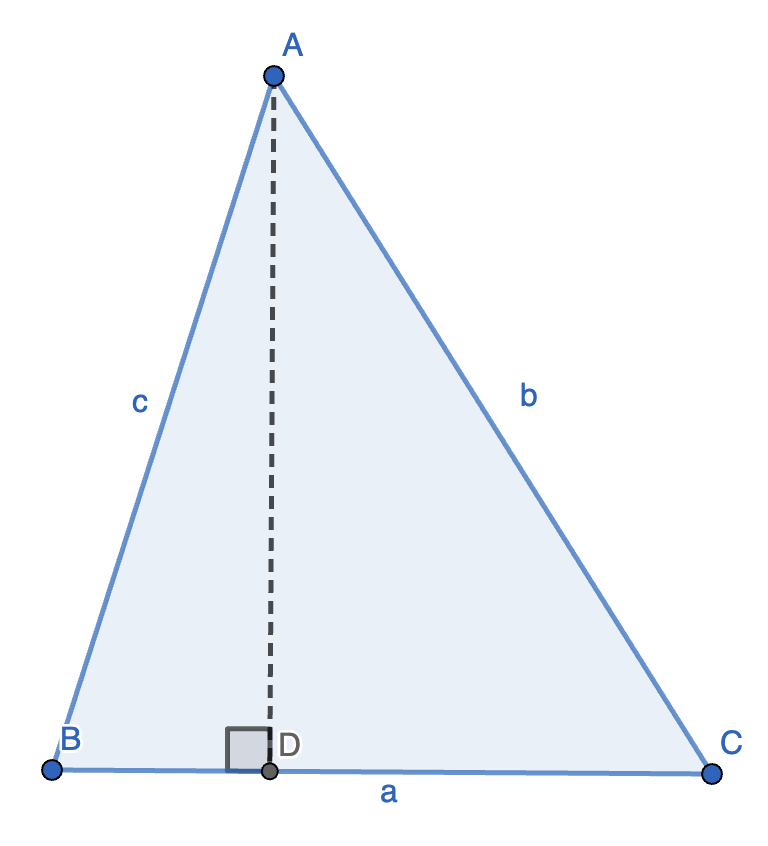
6.（Helen 公式）对于 \(\triangle ABC\)，设 \(p = \dfrac{a + b + c}{2}\)，则其面积为 \(S = \sqrt{p(p - a)(p - b)(p - c)}\)。

证明：根据余弦定理：

\[c^2 = a^2 + b^2 + 2ab \cos C \]

则：

\[\sin \angle CAD = \cos C = \dfrac{a^2 + b^2 - c^2}{2ab} \]

故 \(CD = \dfrac{a^2 + b^2 - c^2}{2a}\)。

又根据勾股定理：

\[\begin{aligned} AD &= \sqrt{b^2 - \left( \dfrac{a^2 + b^2 - c^2}{2a} \right)^2} \\ &= \sqrt{b^2 - \dfrac{(a^2 + b^2 - c^2)^2}{4a^2}} \\ &= \sqrt{\dfrac{4a^2 b^2 - (a^2 + b^2 - c^2)^2}{4a^2}} \\ &= \dfrac{1}{2a} \sqrt{(2ab + a^2 + b^2 - c^2)(2ab - a^2 - b^2 + c^2)} \\ &= \dfrac{1}{2a} \sqrt{(a + b + c)(a + b - c)(a - b + c)(c - a + b)} \end{aligned} \]

故面积为：

\[\begin{aligned} S &= \dfrac{a \cdot AD}{2} \\ &= \dfrac{1}{4} \sqrt{(a + b + c)(a + b - c)(a - b + c)(c - a + b)} \\ &= \sqrt{\dfrac{a + b + c}{2} \cdot \dfrac{a + b - c}{2} \cdot \dfrac{a - b + c}{2} \cdot \dfrac{c - a + b}{2}} \end{aligned} \]

设 \(p = \dfrac{a + b + c}{2}\)，则：

\[\begin{aligned} S &= \sqrt{p(p - c)(p - b)(p - a)} \end{aligned} \]

证毕。

7. 如图，已知 \(\triangle ABC\)，且 \(BD \perp AC\)，设 \(a = BC, b = AC, c = AB, d = AD\)，则 \(a^2 = b^2 + c^2 - 2bd\)。

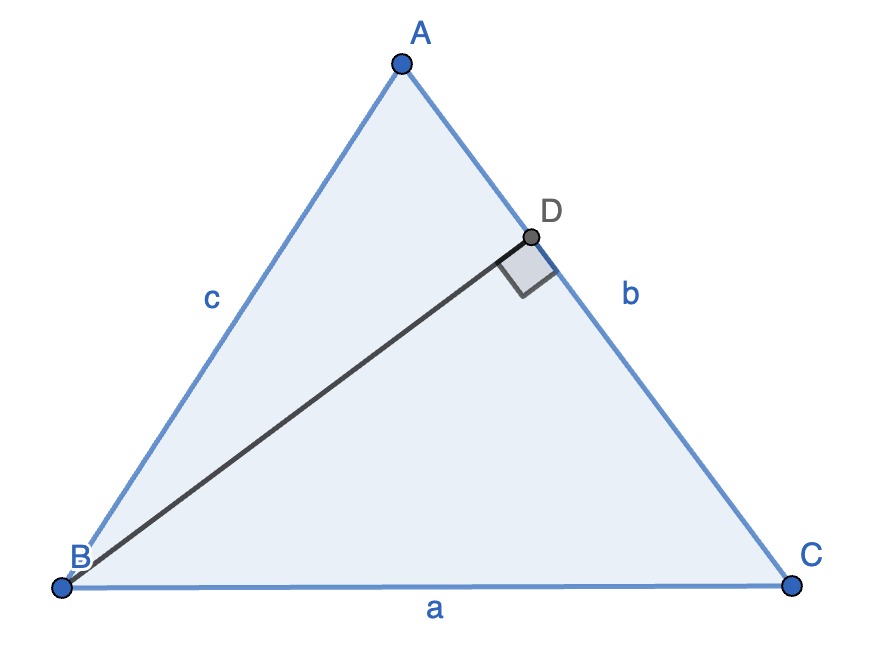
证明：由等差幂线定理：

\[a^2 - c^2 = (b - d)^2 - d^2 \]

则：

\[a^2 = b^2 + c^2 - 2bd \]

证毕。

8.（Stewart 定理）如图，在 \(\triangle ABC\) 中，设 \(BD = m, CD = n, AD = d\)，则 \(b^2 m + c^2 n = a(mn + d^2)\)。

另一种形式：\(AD^2 \cdot BC + AB^2 \cdot CD + AC^2 \cdot DB + BC \cdot CD \cdot DB = 0\)，其中：若线段 \(XY\) 与直线 \(XY\) 的方向相同，则其长度为正，否则长度为负。

记忆方法：将式子改写为 \(man + dad = bmb + cnc\)。

证明 1（余弦定理）：根据余弦定理：

\[\begin{aligned} n^2 + d^2 - 2nd \cos \angle ADC &= b^2 \\ m^2 + d^2 - 2md \cos \angle ADB &= c^2 \end{aligned} \]

则：

\[\begin{aligned} \dfrac{n^2 + d^2 - b^2}{2nd} &= \cos \angle ADC \\ \dfrac{c^2 - m^2 - d^2}{2md} &= \cos \angle ADC \end{aligned} \]

去分母得：

\[\begin{aligned} c^2 n + b^2 m &= (m^2 n + n^2 m) + (d^2 m + d^2 n) \\ &= mn(m + n) + d^2 (m + n) \\ &= (mn + d^2)(m + n) \\ &= a(mn + d^2) \end{aligned} \]

证毕。

证明 2：在直角坐标系上，设点 \(B(a, 0), D(b, 0), C(c, 0), A(x, y)\)。

可以发现：

\[\begin{aligned} & \, (x-a)^2(c-b) + (x-b)^2(a-c) + (x-c)^2(b-a) + (c-b)(a-c)(b-a) \\ =& \, (a-b)(c-b)(a-c) + (c-b)(a-c)(b-a) \\ =& \, 0 \end{aligned} \tag{1} \]

又知：

\[y^2(c-b) + y^2(a-c) + y^2(b-a) = 0 \tag{2} \]

\((1) + (2)\) 得：

\[((x-a)^2+y^2)(c-b) + ((x-b)^2+y^2)(a-c) + ((x-c)^2+y^2)(b-a) + (c-b)(b-a)(a-c) = 0 \]

即 \(AD^2 \cdot BC + AB^2 \cdot CD + AC^2 \cdot DB + BC \cdot CD \cdot DB = 0\)，证毕。

9.（Euler 线）三角形中，外心 \(O\)，重心 \(G\)，垂心 \(H\) 三点共线，且 \(OH = 2OG\)。

10.（Fermat 点）对于 \(\triangle ABC\)：

• 若有内角大于 \(120 \degree\)：设其为 \(\angle A\)，则点 \(A\) 为费马点。

  证明：如图，将 \(\triangle APC\) 逆时针旋转 \(180 \degree - \angle BAC\)，得 \(\triangle AP'C'\)，连接 \(PP'\)。

  

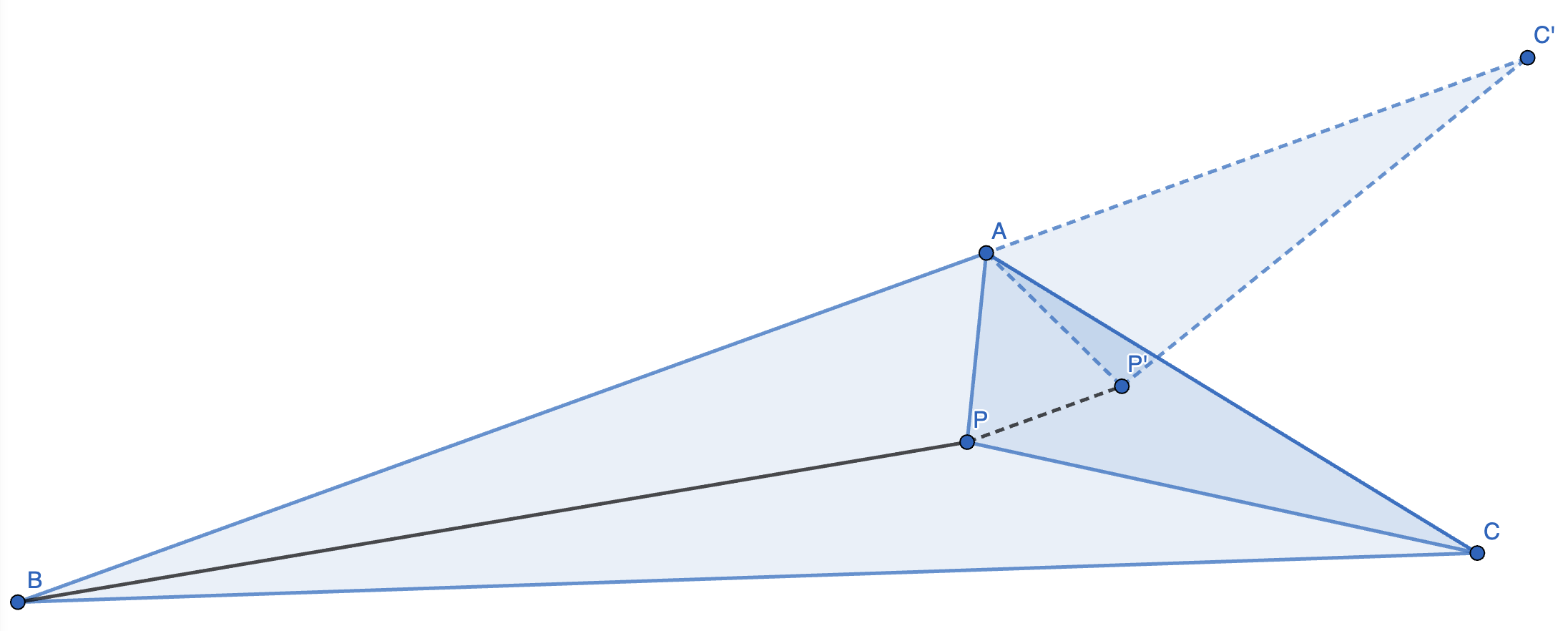
  因为 \(\angle BAC > 120 \degree\)，所以 \(AP > PP'\)。

  则 \(AP + BP + CP \ge BP + PP' + C'P' \ge BC' = AB + AC\)，在 \(A, P, P'\) 重合时取等。

  证毕。

• 否则：对于点 \(P\)，若 \(\angle APB = \angle BPC = \angle CPA = 120 \degree\)，则其为费马点。

  证明 1：如图，将 \(\triangle APC\) 逆时针旋转 \(60 \degree\)，得 \(\triangle AP'C'\)，连接 \(PP'\)。

  

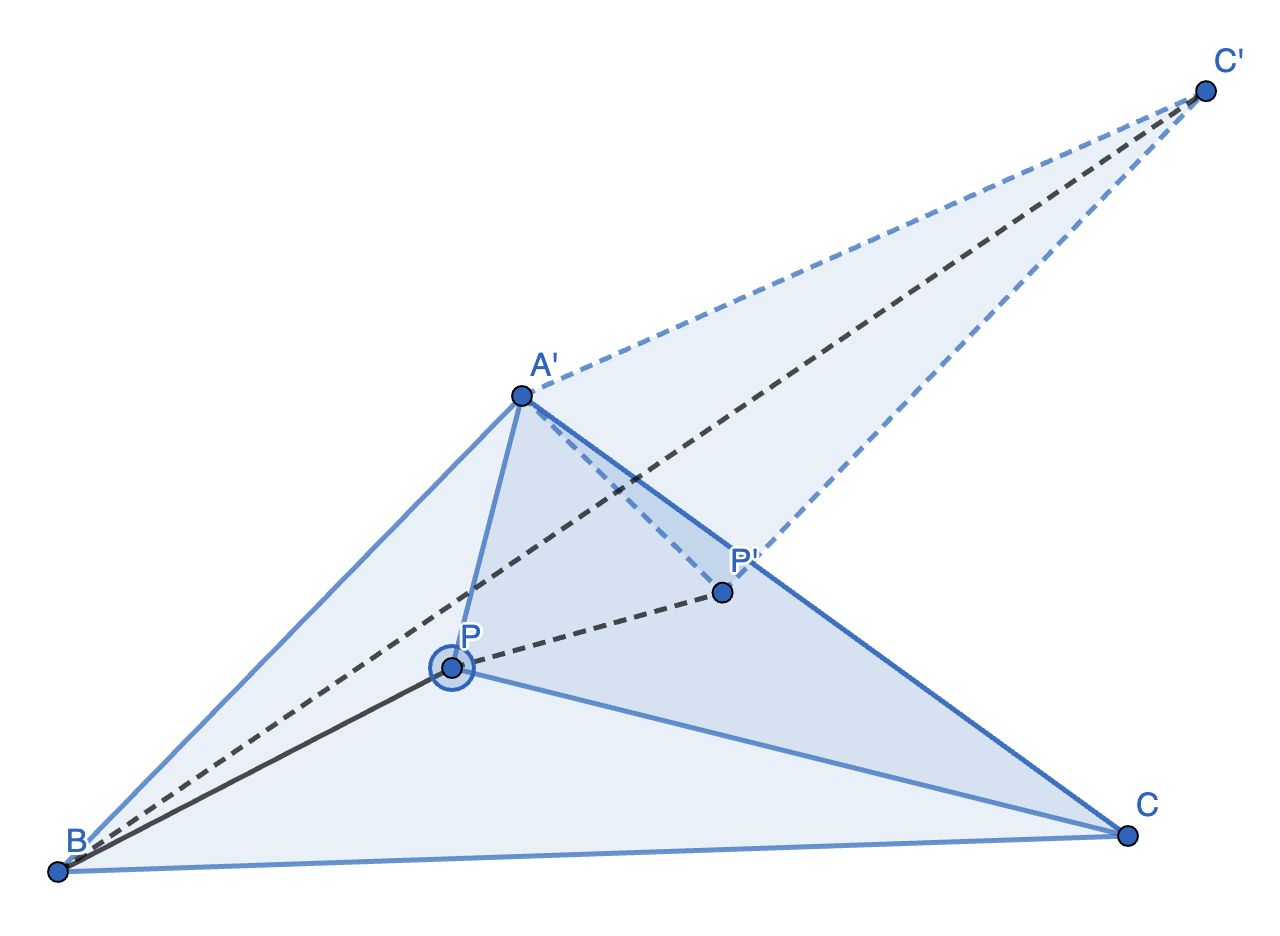
  则 \(AP + BP + CP = BP + PP' + C'P' \ge BC'\)。

  注意到，当 \(B, P, P', C'\) 共线时取等，此时 \(\angle APB = \angle AP'C' = \angle APC = 120 \degree\)，故 \(\angle BPC = 120 \degree\)。

  证毕。

  证明 2：在 \(A, B, C\) 三点分别绑一个绳子，连到一个共同的质点 \(P\) 上。在这三个点上分别挂一个相同重量的重物。

  在平衡状态下，根据最小作用量原理，此时 \(P\) 一定是费马点。

  此时还有三力平衡，则 \(PA\) 一定在 \(\angle BPC\) 的角平分线上，\(PB, PC\) 同理。

  则 \(\angle APB = \angle BPC = \angle CPA = 120 \degree\)，证毕。

11.（Menelaus 定理）在 \(\triangle ABC\) 中，设 \(D, E, F\) 分别在直线 \(AB, AC, BC\) 上。若 \(D, E, F\) 共线，则 \(\dfrac{AD}{BD} \cdot \dfrac{BF}{CF} \cdot \dfrac{CE}{AE} = 1\)。

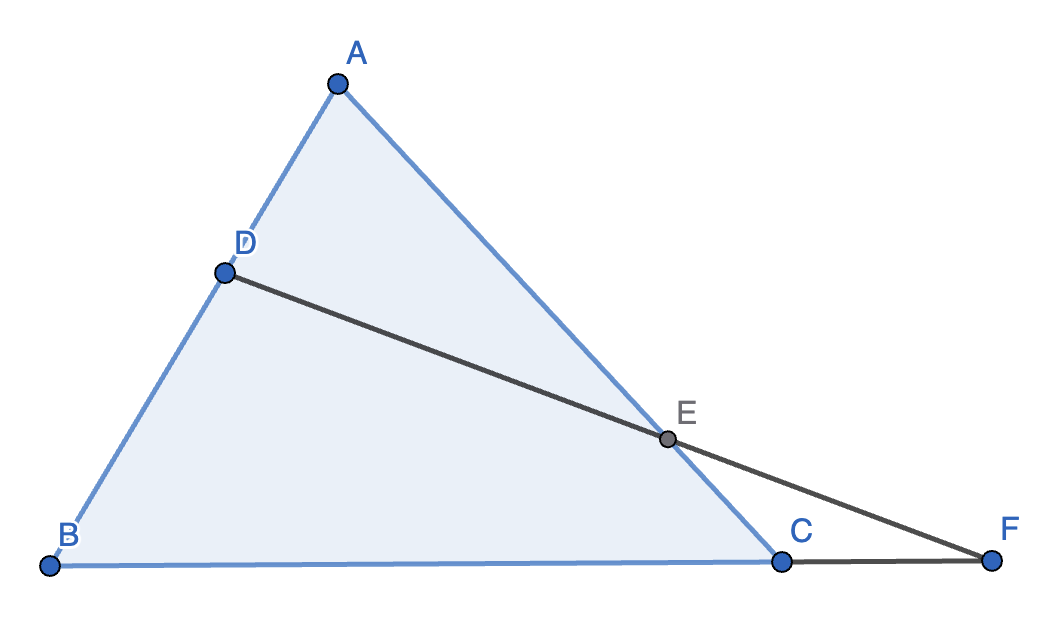
12.（Simson 定理）在 \(\triangle ABC\) 中，设 \(DE \perp AC, DF \perp AB, DG \perp BC\)，则 \(E, F, G\) 共线的充要条件是 \(D\) 在 \(\triangle ABC\) 的外接圆上。

12.（三角形的五心）见此。

0x02. 特殊三角形

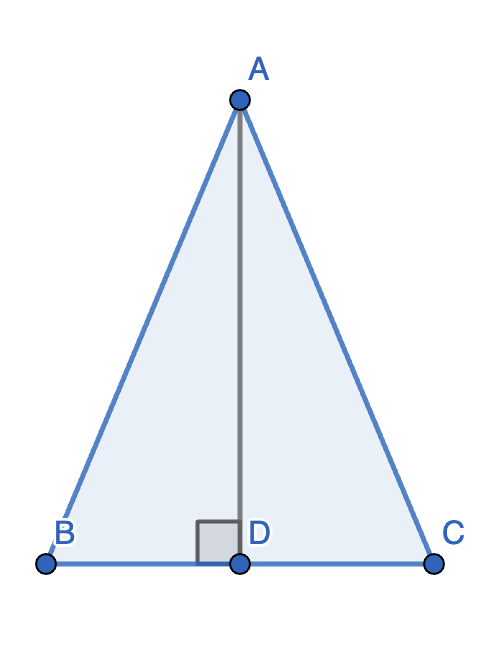
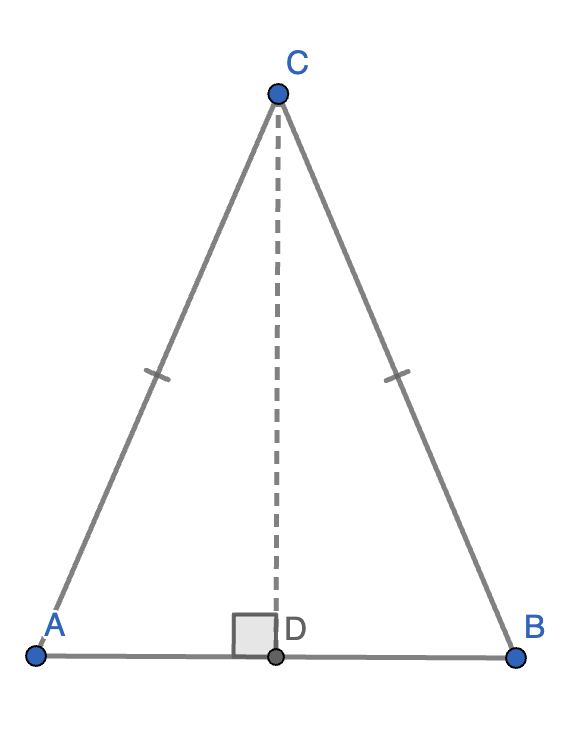
1.（三线合一定理）等腰三角形的顶角平分线、底边中线、底边高线重合。

证明：

如图，\(\triangle ABC\) 为等腰三角形，\(AD\) 为 \(BC\) 上的高。

在 \(\text{Rt} \triangle ABD\) 与 \(\text{Rt} \triangle ACD\) 中，

\[\begin{cases} AD = AD \\ AB = AC \end{cases} \]

故 \(\triangle ABD \cong \triangle ACD\)，则 \(\angle BAD = \angle CAD, BD = CD\)。

这说明 \(AD\) 也是顶角平分线和底边中线，故原命题得证。

1.1.（三线合一定理的逆定理）若三角形的角平分线、对边中线、对边高线三线中有两条重合，那么该三角形为等腰三角形。

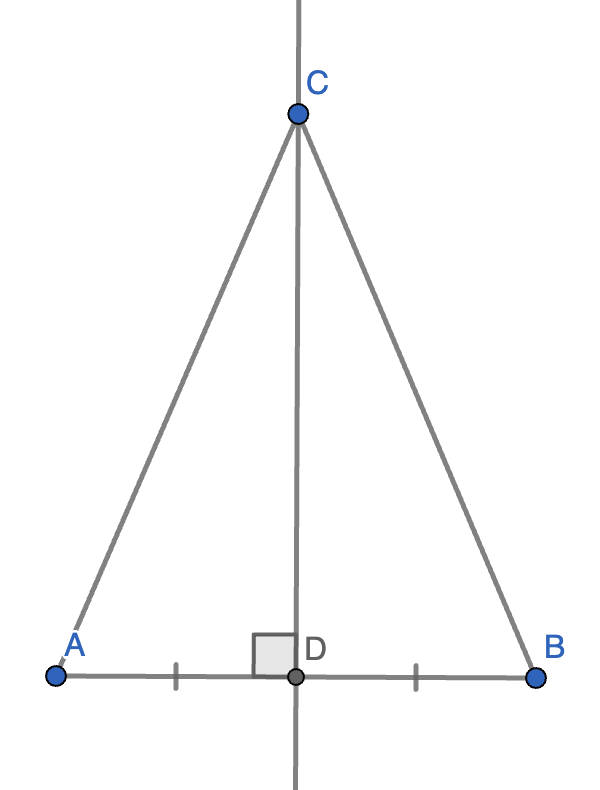
2.（中垂线定理）线段的中垂线上的点和这条线段的两端距离相等，反之亦然。

证明：我们先证明原命题（第 1 部分），再证明它的逆命题（第 2 部分）。

• 第 1 部分：

  如图，已知线段 \(AB\) 以及它的中垂线 \(CD\)。

  因为在 \(\triangle ABC\) 中，\(AB\) 上的高与中线重合，故该三角形为等腰三角形。

  故 \(AC = BC\)，原命题得证。

• 第 2 部分：

  如图，已知线段 \(AB\) 和点 \(C\) 满足 \(AC = BC\)，作 \(CD \perp AB\)。

  容易发现，\(\triangle ABC\) 为等腰三角形，则其底边高线与底边中线重合，则 \(CD\) 也为底边中线。

  这说明 \(CD\) 为 \(AB\) 的中垂线，故原命题得证。

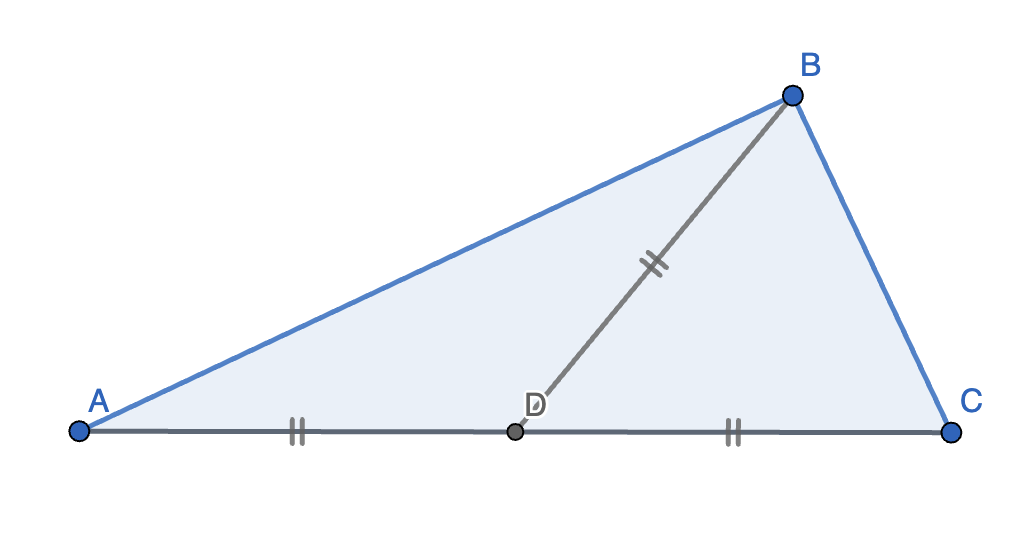
3. 三角形中，若一边上的中线等于该边的一半，则此边所对角为 \(90 \degree\)，反之亦然。

证明：我们先证明原命题（第 1 部分），再证明它的逆命题（第 2 部分）。

• 第 1 部分：

  如图，已知 \(\triangle ABC\) 以及它的中线 \(BD\)。

  容易发现，\(AD = BD = CD\)。

  则 \(\angle B = \angle BAD, \angle C = \angle CAD\)。

  则 \(\angle B + \angle C + \angle BAC = 2(\angle B + \angle C) = 180 \degree\)。

  则 \(\angle BAC = 180 \degree - (\angle B + \angle C) = 90 \degree\)。

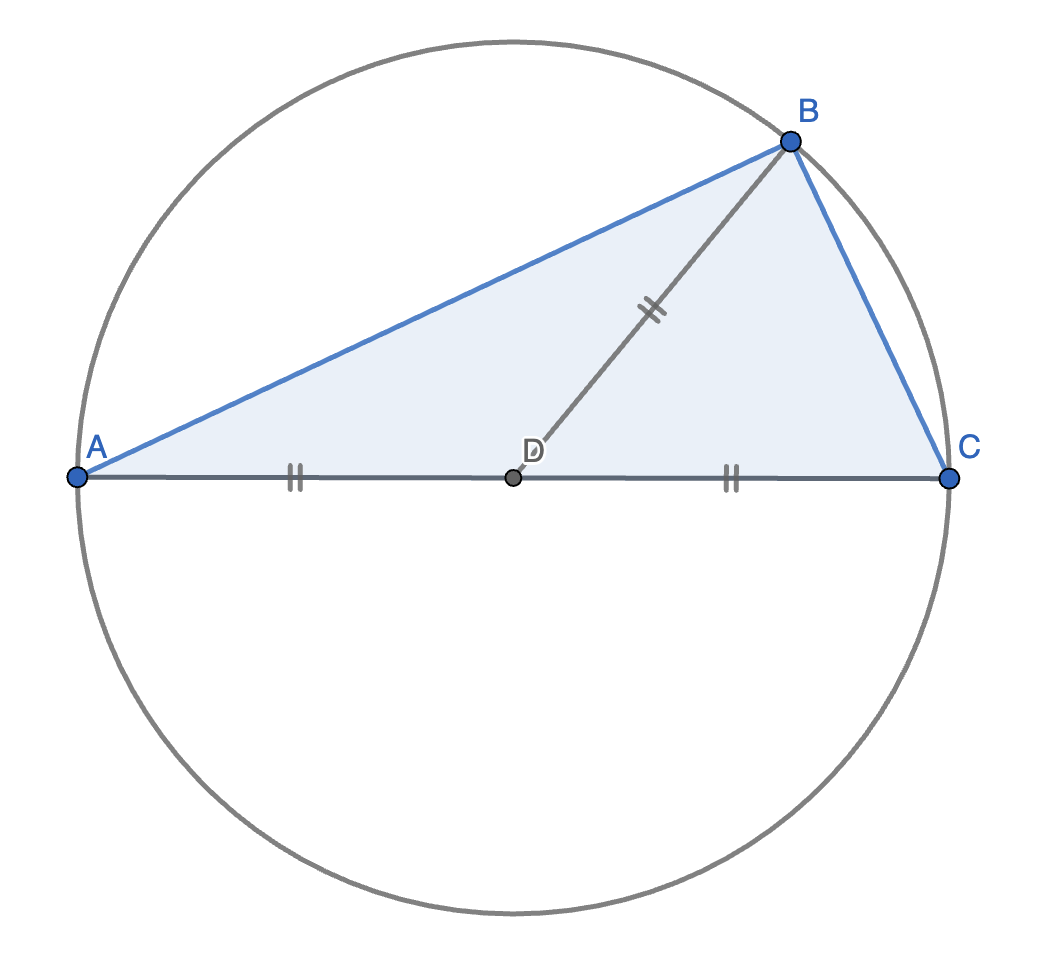
• 第 2 部分：

  如图，已知 \(\text{Rt} \triangle ABC\)、它的中线 \(BD\)、以及它的外接圆 \(\odot D\)。容易发现，\(\angle ABC = 90 \degree\)。

  此时，\(AD, BD, CD\) 均为半径，故原命题得证。

4.（勾股定理）已知 \(\text{Rt} \triangle ABC\)，且 \(a, b < c\)，则 \(a^2 + b^2 = c^2\)。

证明 1：

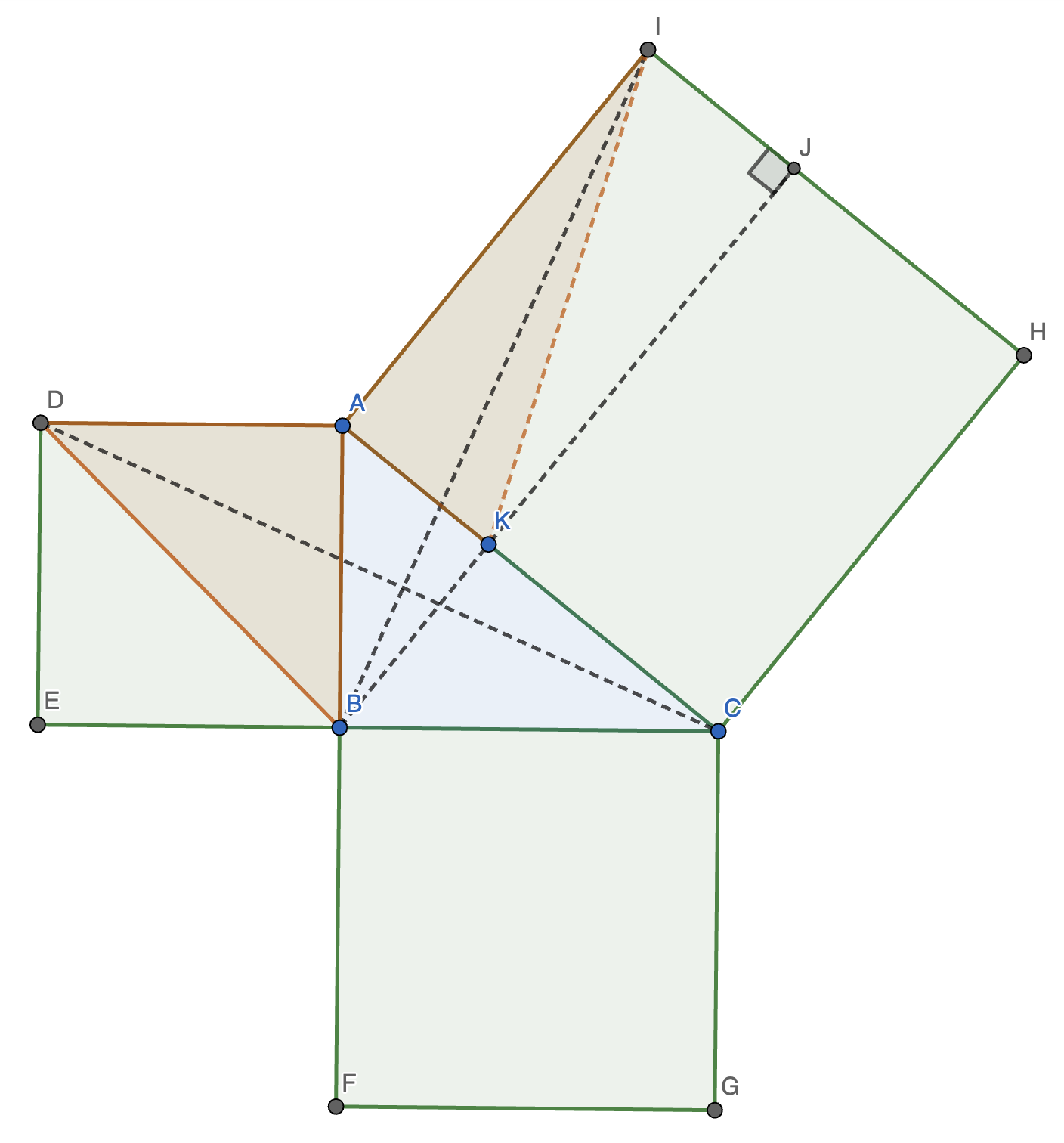
已知 \(\text{Rt} \triangle ABC\)，且 \(\angle ABC = 90 \degree\)。沿 \(AB, BC, AC\) 分别向外作正方形 \(ADEB, BFGC, AIHC\)。连接 \(CD, BI\)，作 \(BJ \perp HI\) 交 \(AC\) 于点 \(K\)。

设 \(a = AB, b = BC, c = AC\)。

此时：

\[\begin{cases} AD = AB \\ \angle CAD = \angle BAI = 90 \degree + \angle BAC \\ AC = AI \end{cases} \]

故 \(\triangle ACD \cong \triangle AIB\)。

又发现 \(S_{\triangle ACD} = \dfrac{1}{2} S_{ABDE}, S_{\triangle AIB} = \dfrac{1}{2} S_{AIJK}\)，则 \(\dfrac{1}{2} S_{ABDE} = \dfrac{1}{2} S_{AIJK} \implies S_{ABDE} = S_{AIJK}\)。

用类似的方法可得 \(S_{BCGF} = S_{CHJK}\)。

故 \(c^2 = S_{AIHC} = S_{AIJK} + S_{CHJK} = S_{ABDE} + S_{BCGF} = a^2 + b^2\)，证毕。

证明 2：

已知正方形 \(BFHG, ACDE\)，且 \(A\) 在 \(BG\) 上，\(C\) 在 \(BF\) 上，\(D\) 在 \(FH\) 上，\(E\) 在 \(GH\) 上。

容易发现：

\[\begin{cases} \angle DEH = \angle CDF \\ DE = CD \\ \angle EDH = \angle DCF \end{cases} \]

则 \(\triangle DEH \cong \triangle DCF\)。同理可得 \(\triangle DEH \cong \triangle DCF \cong \triangle CAB \cong \triangle AEG\)。

设 \(a = AG = EH = DF = BC, b = EG = DH = CF = AB, c = AE = DE = CD = AC\)。

则：

\[S_{BFHG} = S_{ACDE} + S_{\triangle DEH} + S_{\triangle DCF} + S_{\triangle CAB} + S_{\triangle AEG} \]

即：

\[(a + b)^2 = c^2 + 2ab \]

则 \(a^2 + b^2 = c^2\)，原命题成立。

5. 设 \(D\) 是等腰 \(\triangle ABC\) 的底边 \(BC\) 上任意一点，则 \(AD^2 = AB^2 - BD \cdot CD\)。

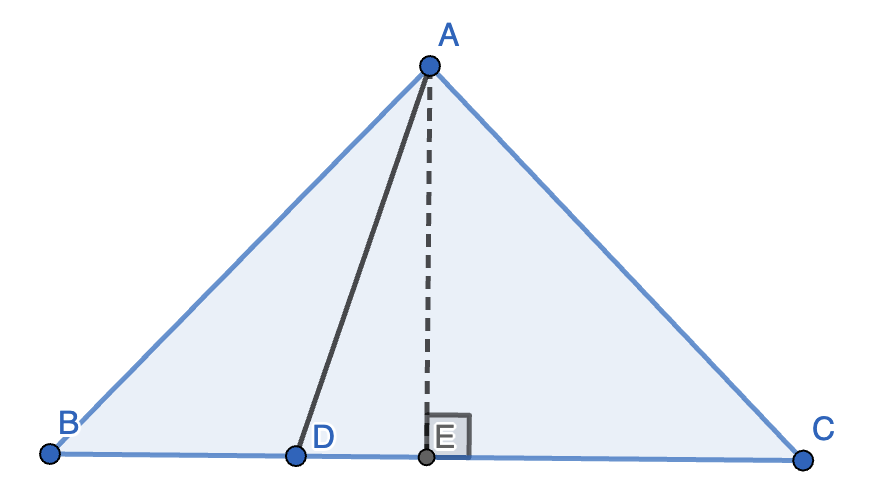
证明：

\[\begin{aligned} DE^2 = DE^2 &\implies DE^2 = BE^2 - BE^2 + DE^2 \\ &\implies AE^2 + DE^2 = AE^2 + BE^2 - BE^2 + DE^2 \\ &\implies AD^2 = AB^2 - (BE - DE)(BE + DE) \\ &\implies AD^2 = AB^2 - BD(CE + DE) \\ &\implies AD^2 = AB^2 - BD \cdot CD \end{aligned} \]

证毕。

5.1.（圆幂定理）设 \(D\) 是等腰 \(\triangle ABC\) 的底边 \(BC\)（直线）上任意一点，则 \(|AD^2 - AB^2| = BD \cdot CD\)。

6. 边长为 \(l\) 的等边三角形的面积为 \(S = \dfrac{\sqrt{3}}{4} l^2\)。

0x03. 圆

1. 已知 \(\triangle ABC\) 的边长 \(a, b, c\) 满足 \(a^2 + b^2 = c^2\)，则其内切圆的半径为 \(r = \dfrac{ab}{a + b + c}\)。

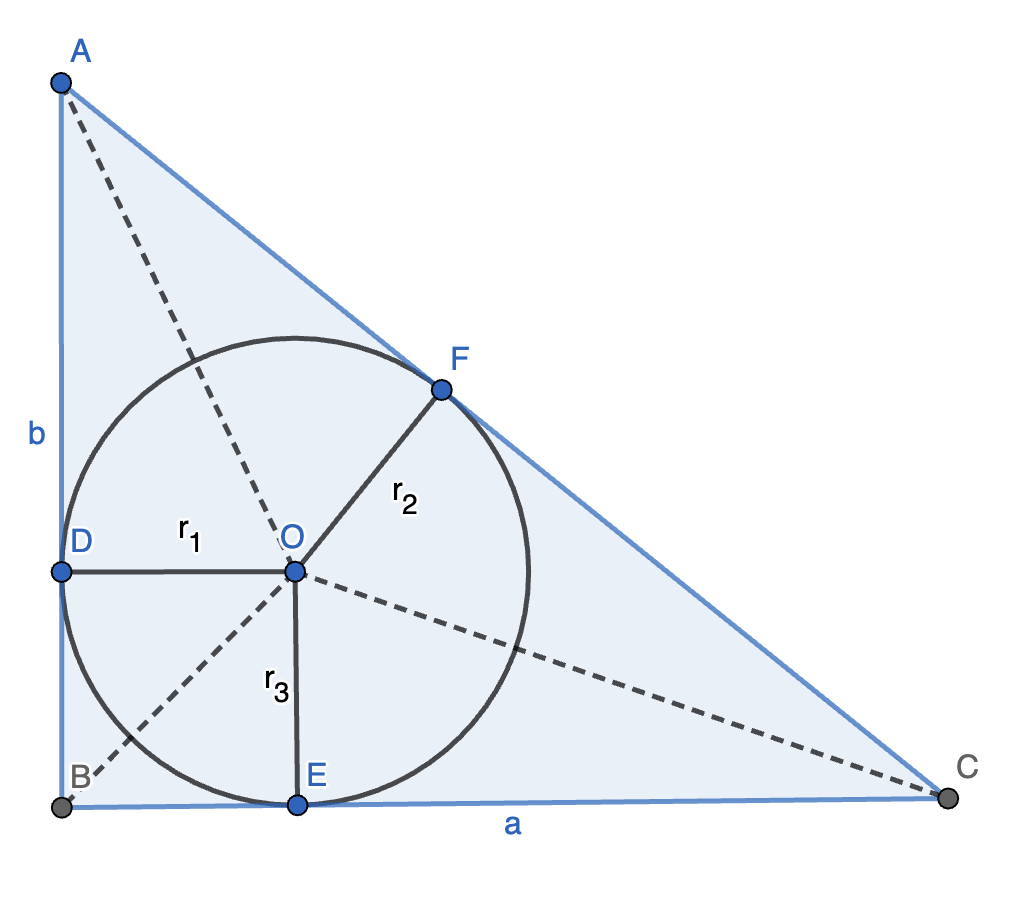
证明（面积法）：容易发现，\(AB \perp OD, BC \perp OE, AC \perp OF\)。则

\[\begin{aligned} 2S_{\triangle AOB} + 2S_{\triangle BOC} + 2S_{\triangle AOC} &= (AB \cdot OD + BC \cdot OE + AC \cdot OF) \\ &= (a + b + c) r \\ &= ab \\ &= 2S_{\triangle ABC} \end{aligned} \]

则 \(r = \dfrac{ab}{a + b + c}\)，原命题得证。

1.1. \(\triangle ABC\) 的内切圆的半径为 \(r = \dfrac{2S_{\triangle ABC}}{a + b + c}\)。

2.（圆周角定理）在圆 \(O\) 上有 \(A, B, C\) 三点，满足三点互不重合，且 \(C\) 不在弧 \(AB\) 上。连接 \(AC, BC, AO, BO\)。证明：\(\angle AOB = 2 \angle ACB\)。

证明 ^[4]：作 \(CO\) 及其延长线交圆 \(O\) 于点 \(D\)。此时有两种情况：

• \(O\) 在 \(\triangle ABC\) 内部：容易发现，\(AC = AO, \angle ACO = \angle CAO\)，则外角 \(\angle AOD = \angle ACO + \angle CAO = 2 \angle ACO\)。

  同理，\(\angle BOD = 2 \angle BCO\)，则 \(\angle AOB = \angle AOD + \angle BOD = 2 (\angle ACO + \angle BCO) = 2 \angle ACB\)。

• \(O\) 在 \(\triangle ABC\) 外部：容易发现，\(AO = BO = CO, \angle ACO = \angle CAO, \angle BCO = \angle CBO\)。

  则外角 \(\angle AOD = \angle ACO + \angle CAO = 2 \angle ACO, \angle BOD = \angle BCO + \angle CBO = 2 \angle BCO\)。

  则 \(\angle AOB = \angle BOD - \angle AOD = 2 (\angle BCO - \angle ACO) = 2 \angle ACB\)。

故原命题得证。

2.1. 在圆中，直径所对圆周角为 \(90 \degree\)。

证明：

可以发现，\(\angle ABC = \dfrac{1}{2} \angle ADC = 90 \degree\)，故原命题得证。

3.（垂径定理）已知圆的弦 \(AB\) 与一条直线 \(CD\)。则下方结论知二推三：

• \(CD\) 过圆心。
• \(CD \perp AB\)。
• \(CD\) 平分 \(\overparen{AB}\)。
• \(CD\) 平分 \(AB\)。
• \(CD\) 平分 \(\overparen{AB}\) 所对的弧。

4.（切线长定理）设 \(AP, BP\) 为圆外一点 \(P\) 向圆作的切线，且圆心为 \(O\)，则 \(AP = BP, \angle APO = \angle BPO\)。

证明：因为 \(\angle OAP = \angle OBP = 90 \degree, OP = OP, OA = OB\)，所以 \(\triangle AOP \cong \triangle BOP\)。证毕。

5.（弦切角定理）在 \(B\) 上作 \(\odot A\) 的切线 \(l\)，在 \(\odot A\) 上任取一点 \(C\)，连接 \(BC\)，则 \(l\) 与 \(BC\) 的夹角为 \(\dfrac{1}{2} \angle BAC\)。

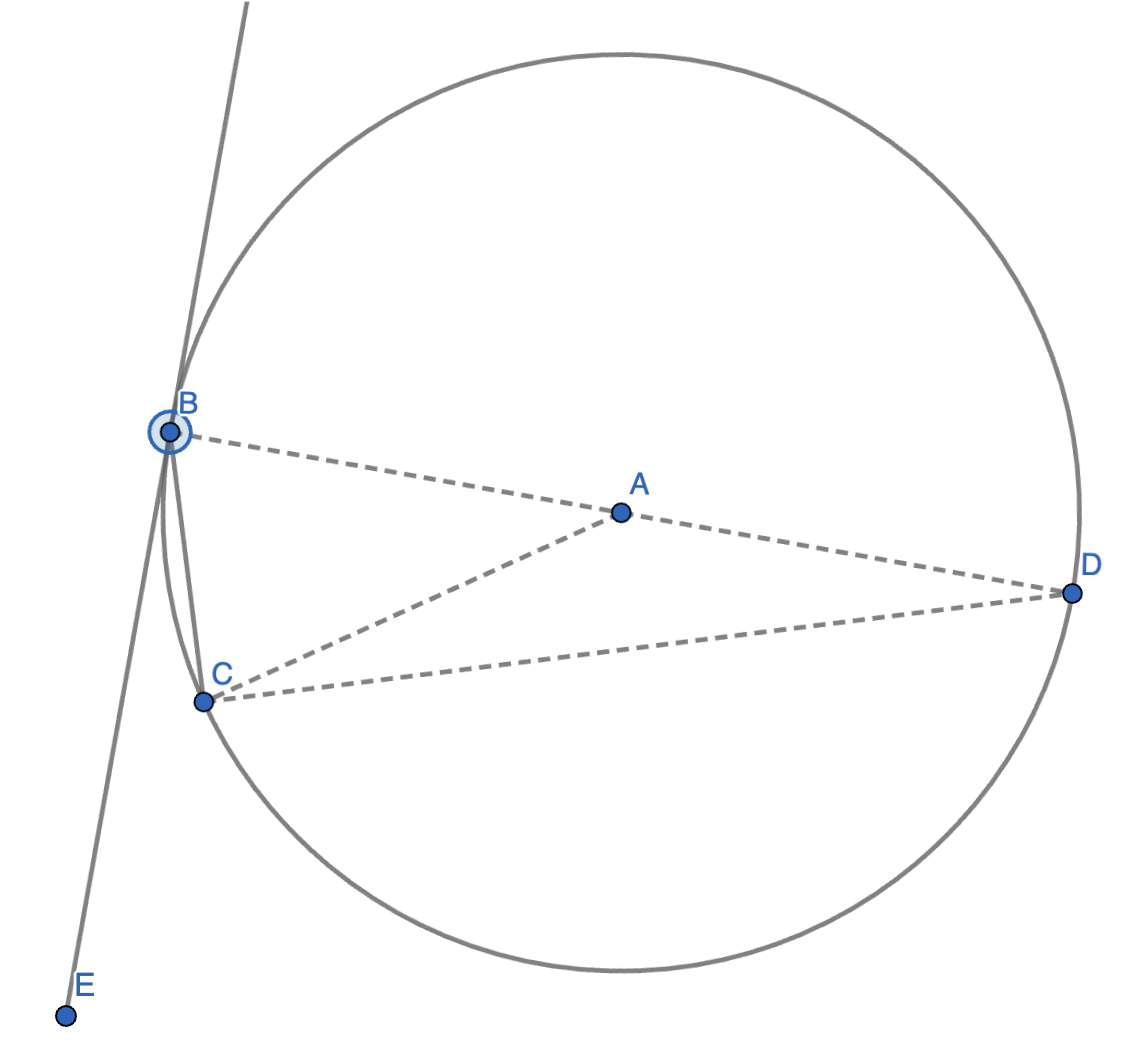
证明：作 \(CD \perp BC\) 交 \(\odot A\) 于 \(D\)，则 \(BD\) 过点 \(A\)。连接 \(AC, BD\)。

设 \(l\) 与 \(BC\) 的夹角为 \(\alpha\)。

则 \(\alpha + \angle ABC = \angle BDC + \angle ABC = \dfrac{1}{2} \angle BAC + \angle ABC = 90 \degree\)，故 \(\alpha = \dfrac{1}{2} \angle BAC\)。

证毕。

6.（相交弦定理）给定 \(\odot O\)，\(AB, CD\) 为 \(\odot O\) 的两条弦，\(AB, CD\) 交于点 \(P\)。则 \(PA \cdot PB = PC \cdot PD\)。

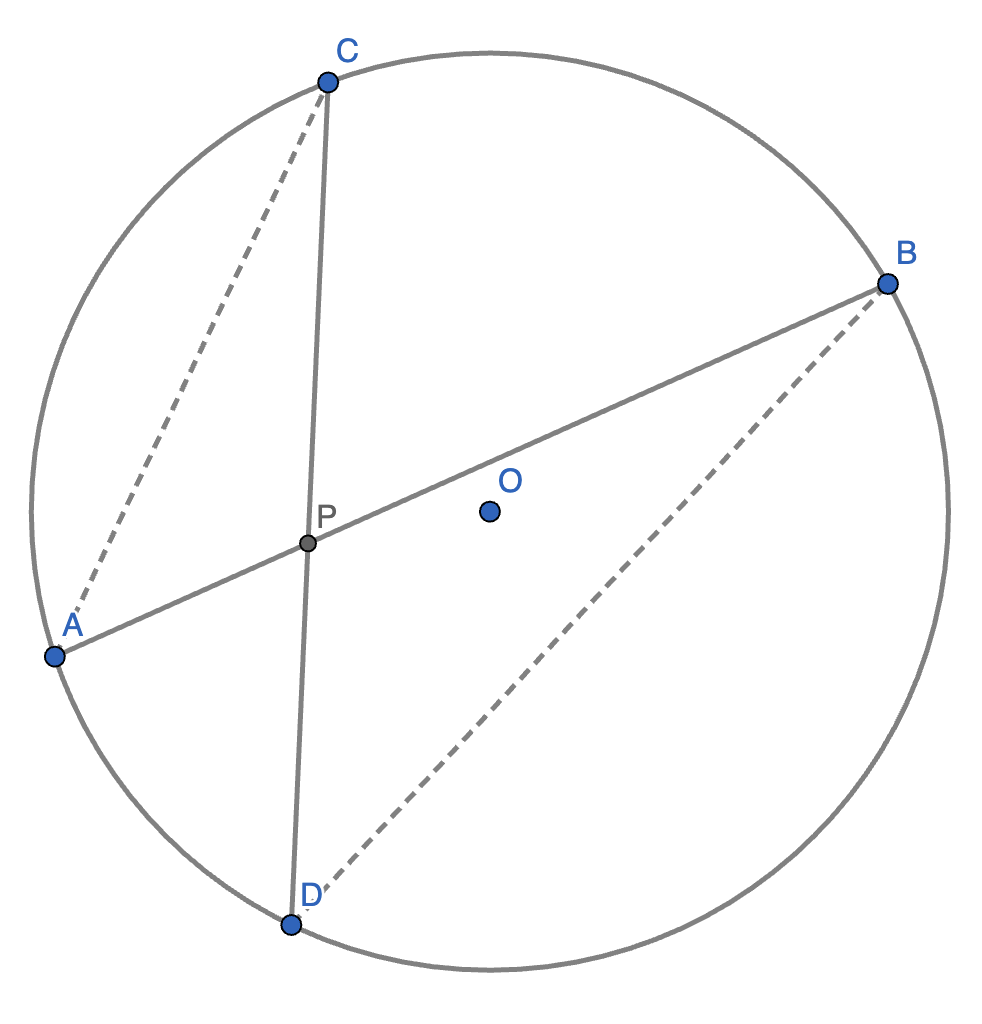
证明：容易发现，\(\angle APC = \angle BPD\)，则 \(\triangle APC \sim \triangle BPD\)，则 \(\dfrac{PA}{PC} = \dfrac{PD}{PB}\)，故 \(PA \cdot PB = PC \cdot PD\)。

证毕。

7.（切割线定理）设 \(PA, PB\) 为 \(\odot O\) 的割线，\(PT\) 为 \(\odot O\) 的切线，且 \(P, A, B\) 三点共线，则 \(PT^2 = PA \cdot PB\)。

8.（四点共圆的判定）

• 若四边形 \(ABCD\) 满足对角之和为 \(180 \degree\)，则 \(A, B, C, D\) 四点共圆。

• （圆周角定理的逆定理）若三角形 \(\triangle ABC\) 与 \(\triangle ABD\) 有公共边 \(AB\)，且 \(\angle C = \angle D\)，且 \(C\) 与 \(D\) 在 \(AB\) 的同侧，则 \(A, B, C, D\) 四点共圆。

• （相交弦定理的逆定理）若线段 \(AB, CD\) 交于点 \(P\)，且 \(AP \cdot BP = CP \cdot DP\)，那么 \(A, B, C, D\) 四点共圆。

  证明：

  

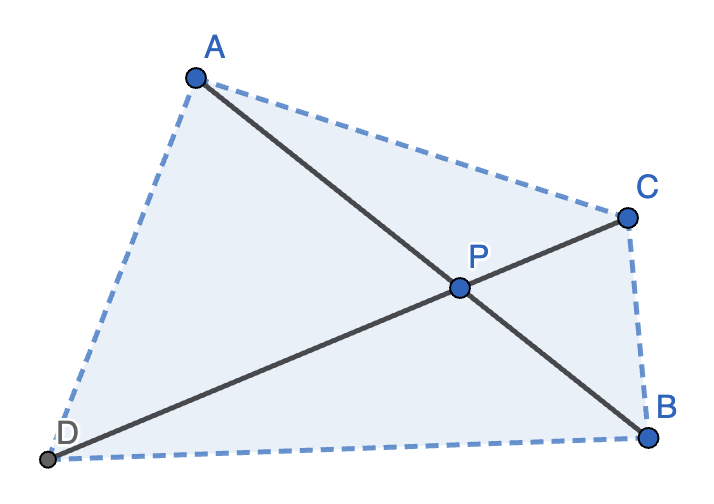
  注意到 \(\dfrac{AP}{DP} = \dfrac{CP}{BP}\)，则 \(\triangle APD \sim \triangle CPB \implies \angle DAP = \angle BCP\)。

  又知 \(A, C\) 皆在 \(BD\) 同侧，故证毕。

9. 设 \(\odot O\) 的半径为 \(r\)，其上有一弧 \(AB\)，长度为 \(l\)，角度为 \(\theta\)，则 \(AB = 2r \sin(\theta / 2) = \dfrac{2l \sin(\theta / 2)}{\theta}\)。

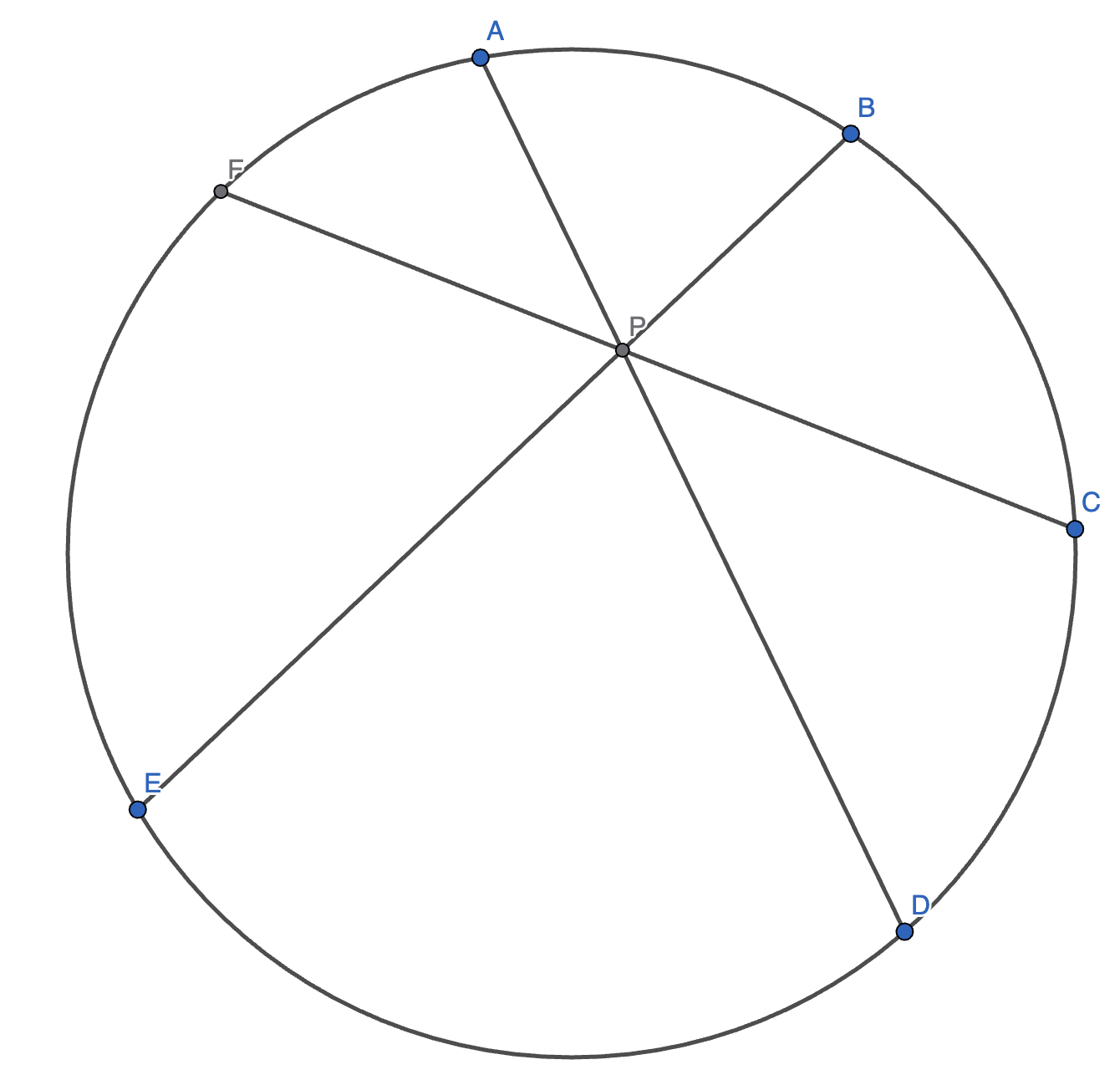
10.（三弦共点定理 / 圆中 Ceva 定理）如图，设弧 \(AB, BC, CD, DE, EF, FA\) 所对的圆周角分别为 \(\alpha_1, \alpha_2, \cdots, \alpha_6\)，则 \(AD, BE, CF\) 共点的充要条件为：

\[\dfrac{\sin(\alpha_1)}{\sin(\alpha_2)} \cdot \dfrac{\sin(\alpha_3)}{\sin(\alpha_4)} \cdot \dfrac{\sin(\alpha_5)}{\sin(\alpha_6)} = 1 \]

即：

\[\dfrac{AB}{BC} \cdot \dfrac{CD}{DE} \cdot \dfrac{EF}{FA} = 1 \]

0x04. 四边形

1. 已知长方形 \(ABCD\)，点 \(E\) 在直线 \(AD, BC\) 之间，连接 \(AE, BE, CE, DE\)。则 \(AE^2 + CE^2 = BE^2 + DE^2\)。

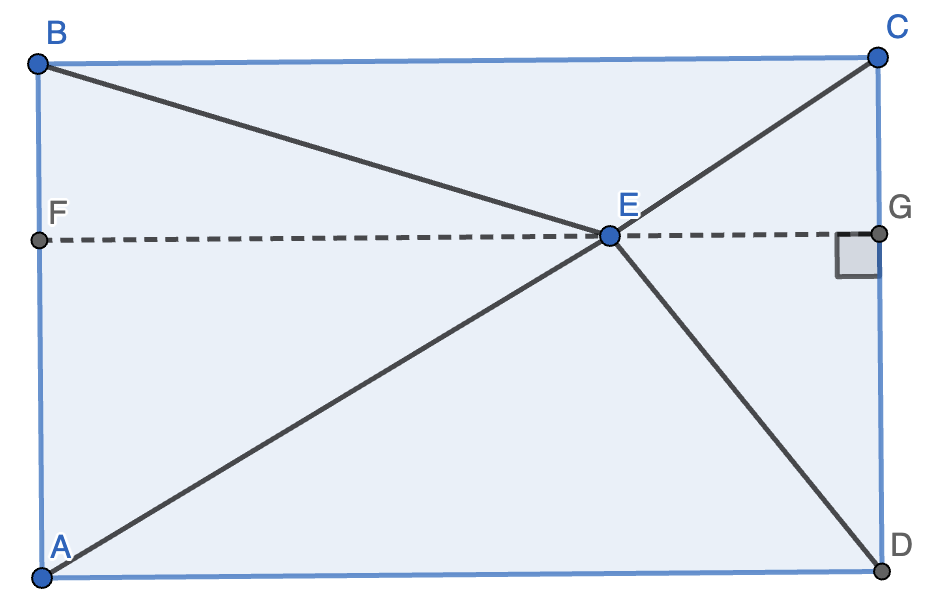
证明：我们只需证明 \(AE^2 - BE^2 = DE^2 - CE^2\)。

容易发现，\(AE^2 - BE^2 = AF^2 - BF^2 = DG^2 - CG^2 = DE^2 - CE^2\)。

证毕。

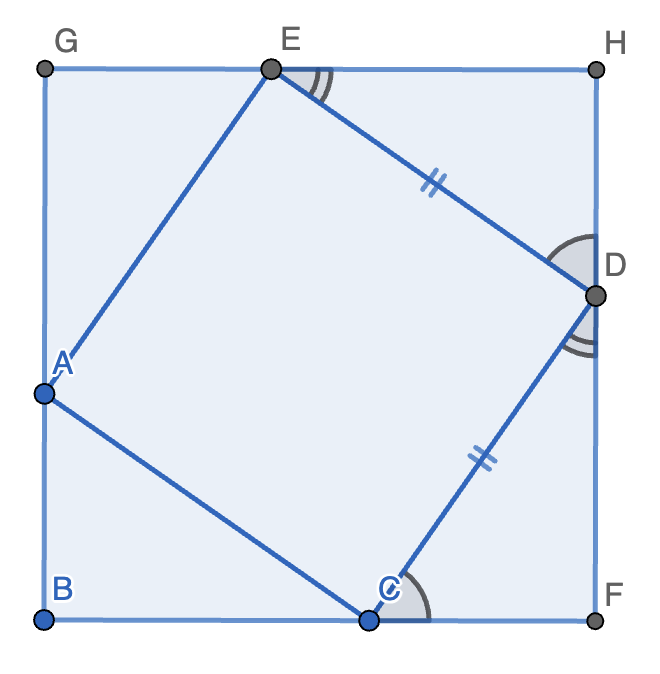
2.（Ptolemy 定理）设 \(\angle BAC = \alpha, \angle DAC = \beta\)，则 \(A, B, C, D\) 共圆的充要条件是 \(AB \cdot CD + AD \cdot BC = AC \cdot BD\)，即 \(AC \sin(\alpha + \beta) = AD \sin(\alpha) + AB \sin(\beta)\)。

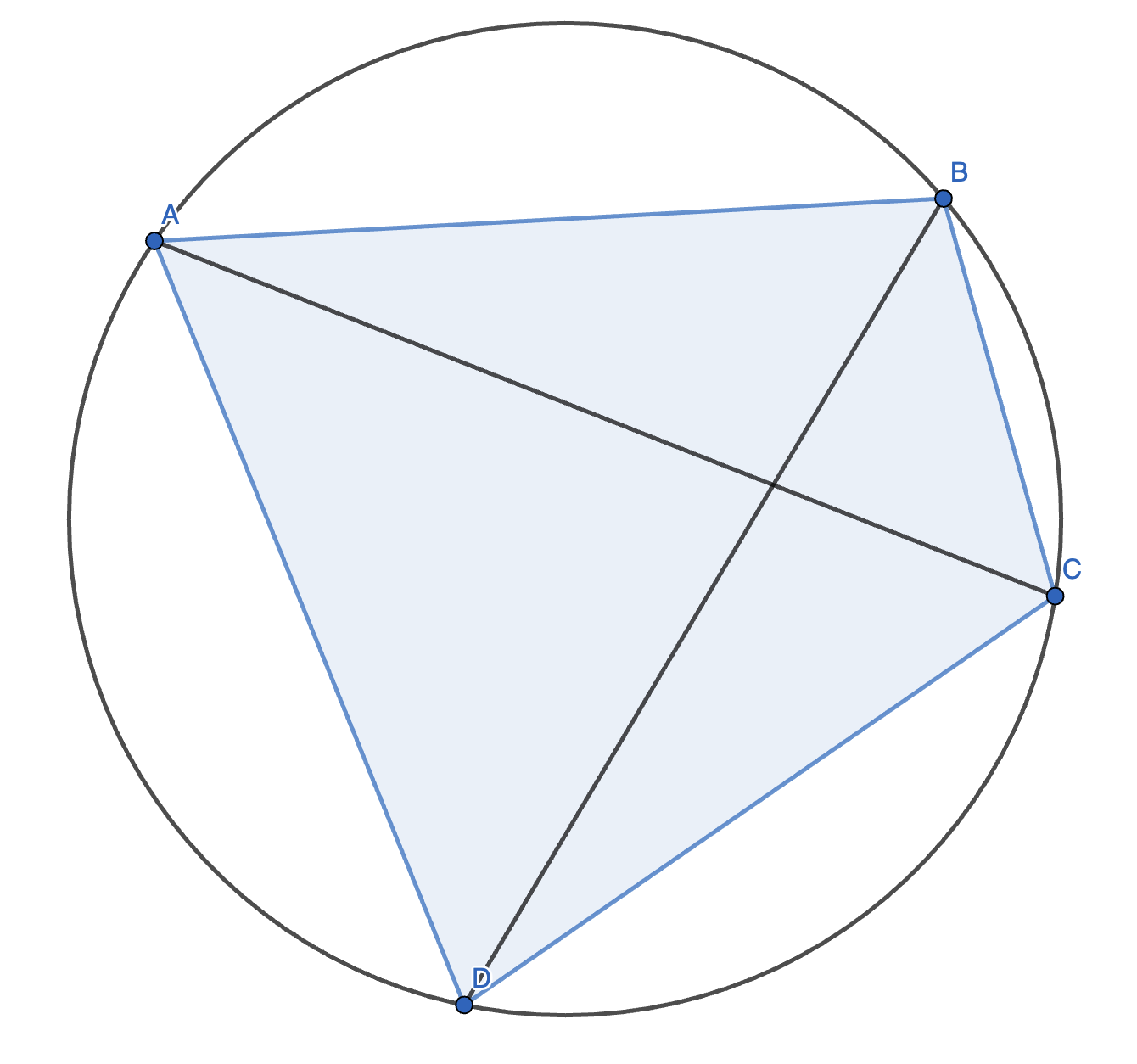
2.1.（广义 Ptolemy 定理）任意四边形 \(ABCD\) 一定满足 \(AD \cdot BC + AB \cdot CD \ge AC \cdot BD\)。

0x05. 三角函数

1. 在平面直角坐标系中给定单位圆（圆心在原点，半径为 \(1\)），则以 \((1, 0)\) 为一端点，对应角度为 \(\theta\) 的弧（逆时针）的另一端点为 \((\cos \theta, \sin \theta)\)。

2.（三角形的面积公式）三角形 \(\triangle ABC\) 的面积为 \(S = \dfrac{1}{2} ab \sin C = \dfrac{1}{2} bc \sin A = \dfrac{1}{2} ac \sin B\)。

证明：

如图，作 \(AD \perp BC\)，设 \(h = AD\)，则 \(\sin C = \dfrac{h}{b}, S = \dfrac{1}{2} ah = \dfrac{1}{2} ab \sin C\)。

同理可得 \(S = \dfrac{1}{2} bc \sin A, S = \dfrac{1}{2} ac \sin B\)。

证毕。

3.（正弦定理）如图，已知三角形 \(\triangle ABC\)，则 \(\dfrac{a}{\sin A} = \dfrac{b}{\sin B} = \dfrac{c}{\sin C}\)。

证明：容易发现：

\[S_{\triangle ABC} = \dfrac{1}{2} bc \sin A = \dfrac{1}{2} ac \sin B \]

则：

\[b \sin A = a \sin B \]

即：

\[\dfrac{a}{\sin A} = \dfrac{b}{\sin B} \]

同理可证 \(\dfrac{a}{\sin A} = \dfrac{c}{\sin C}\)，证毕。

4.（分角定理）已知 \(\triangle ABD\)，\(C\) 在 \(BD\) 上，连接 \(AC\)，则 \(\dfrac{BD}{CD} = \dfrac{AB \sin \angle BAD}{AC \sin \angle CAD}\)。

证明：从面积入手：

\[\begin{aligned} S_{\triangle CAD} = \dfrac{1}{2} AC \cdot AD \sin \angle CAD \\ S_{\triangle ABD} = \dfrac{1}{2} AB \cdot AD \sin \angle BAD \\ \end{aligned} \]

故：

\[\dfrac{S_{\triangle CAD}}{S_{\triangle ABD}} = \dfrac{AC \sin \angle CAD}{AB \sin \angle BAD} = \dfrac{BD}{CD} \]

证毕。

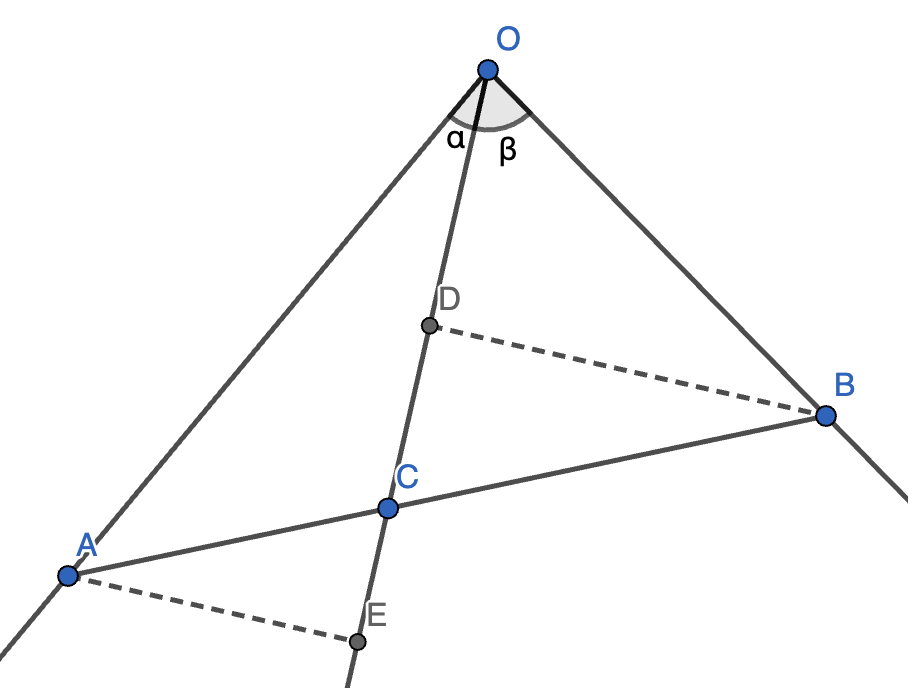
5.（张角定理）已知射线 \(OA, OB, OC\)，\(C\) 在 \(\angle AOB\) 内，设 \(\alpha = \angle AOC, \beta = \angle BOC\)，则 \(A, B, C\) 共线的充要条件为 \(\dfrac{\sin \beta}{OA} + \dfrac{\sin \alpha}{OB} = \dfrac{\sin(\alpha + \beta)}{OC}\)。

证明：作 \(AE \perp OC, BD \perp OC\)。

根据条件可得 \(\dfrac{OB \sin \beta + OA \sin \alpha}{OA \cdot OB} = \dfrac{\sin(\alpha + \beta)}{OC}\)，即 \(OB \cdot OC \sin \beta + OA \cdot OC \sin \alpha = OA \cdot OB \sin(\alpha + \beta)\)。

此式告诉我们：\(S_{\triangle BOC} + S_{\triangle AOC} = S_{\triangle AOB}\)，故 \(A, B, C\) 三点共线，原命题成立。

6.（余弦定理）已知 \(\triangle ABC\)，则 \(a^2 = b^2 + c^2 - 2bc \cos A, b^2 = a^2 + c^2 - 2ac \cos B, c^2 = a^2 + b^2 - 2ab \cos C\)。

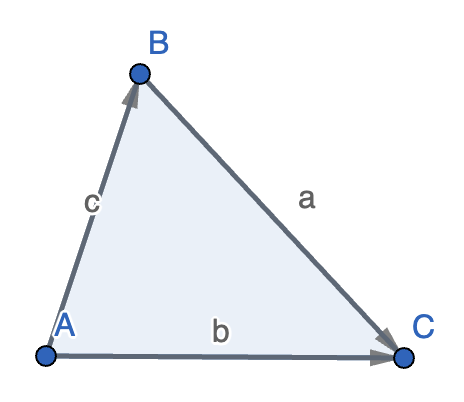
证明（向量法）：

我们只证明 \(c^2 = a^2 + b^2 - 2ab \cos C\)，其它的证明类似。

容易发现：

\[\begin{aligned} \vec{c}^2 &= (\vec{a} - \vec{b})^2 \\ &= \vec{a}^2 + \vec{b}^2 - 2\vec{a} \cdot \vec{b} \\ &= \vec{a}^2 + \vec{b}^2 - 2 |\vec{a}| |\vec{b}| \cos C \\ \end{aligned} \]

则 \(|\vec{c}|^2 = |\vec{a}|^2 + |\vec{b}|^2 - 2 |\vec{a}| |\vec{b}| \cos C\)，即 \(c^2 = a^2 + b^2 - 2ab \cos C\)。

7.（常用恒等式）

• （勾股定理）\(\sin^2(x) + \cos^2(x) = 1, \tan^2(x) + 1 = \sec^2(x)\)。
• \((\sin(x) \pm \cos(x))^2 = 1 \pm 2 \sin(x) \cos(x) = 1 \pm \sin(2x)\)。
• \((\sin(x) + \cos(x))^2 + (\sin(x) - \cos(x))^2 = 2\)。
• （诱导公式）

  \(x\)	\(\sin(x)\)	\(\cos(x)\)	\(\tan(x)\)
  \(-x\)	\(-\sin(x)\)	\(\cos(x)\)	\(-\tan(x)\)
  \(\pi / 2 - x\)	\(\cos(x)\)	\(\sin(x)\)	\(\cot(x)\)
  \(\pi / 2 + x\)	\(-\cos(x)\)	\(\sin(x)\)	\(-\cot(x)\)
  \(\pi + x\)	\(-\sin(x)\)	\(-\cos(x)\)	\(\tan(x)\)
  \(\pi - x\)	\(\sin(x)\)	\(-\cos(x)\)	\(-\tan(x)\)

• （特殊角）

  \(x\)	\(\sin(x)\)	\(\cos(x)\)	\(\tan(x)\)
  \(0\)	\(0\)	\(1\)	\(0\)
  \(\pi / 6\)	\(1 / 2\)	\(\sqrt{3} / 2\)	\(\sqrt{3} / 3\)
  \(\pi / 4\)	\(\sqrt{2} / 2\)	\(\sqrt{2} / 2\)	\(1\)
  \(\pi / 3\)	\(\sqrt{3} / 2\)	\(1 / 2\)	\(\sqrt{3}\)
  \(\pi / 2\)	\(1\)	\(0\)	\(-\)

• （两角和差）
  • \(\cos(x \pm y) = \cos(x) \cos(y) \mp \sin(x) \sin(y)\)。
  • \(\sin(x \pm y) = \sin(x) \cos(y) \pm \cos(x) \sin(y)\)。

  证明：

  \[\begin{aligned} e^{i(x + y)} &= \cos(x + y) + i \sin(x + y) \\ e^{i(x + y)} &= e^{ix} \cdot e^{iy} \\ &= (\cos(x) + i \sin(x))(\cos(y) + i \sin(y)) \\ &= (\cos(x) \cos(y) - \sin(x) \sin(y)) + i \cdot (\sin(x) \cos(y) + \cos(x) \sin(y)) \end{aligned} \]

  比较各系数得 \(\cos(x + y) = \cos(x) \cos(y) - \sin(x) \sin(y), \sin(x + y) = \sin(x) \cos(y) + \cos(x) \sin(y)\)。

  \(x - y\) 时的证明类似，证毕。

  • \(\tan(x \pm y) = \dfrac{\tan(x) \pm \tan(y)}{1 \mp \tan(x) \tan(y)}\)。
• （\(n\) 倍角公式）
  • \(\cos(nx) = 2^{n - 1} \prod \limits_{k = 0}^{n - 1} \sin \left(x + \dfrac{(2k + 1) \pi}{2n} \right) \quad (n \in \mathbb{N}^+)\)。
  • \(\sin(nx) = 2^{n - 1} \prod \limits_{k = 0}^{n - 1} \sin \left(x + \dfrac{k \pi}{n} \right) \quad (n \in \mathbb{N}^+)\)。
  • （常用特例）\(\sin(2x) = 2 \sin(x) \cos(x), \cos(2x) = \cos^2(x) - \sin^2(x) = 1 - 2 \sin^2(x) = 2 \cos^2(x) - 1\)。
• （辅助角公式）\(a \sin(x) + b \cos(x) = \sqrt{a^2 + b^2} \sin(x + y)\)，其中 \(y\) 满足 \(\cos(y) = \dfrac{a}{\sqrt{a^2 + b^2}}, \sin(y) = \dfrac{b}{\sqrt{a^2 + b^2}}\)。
• （降幂公式）
  • \(\cos^2(x) = \dfrac{1 + \cos(2x)}{2}\)。
  • \(\sin^2(x) = \dfrac{1 - \cos(2x)}{2}\)。
  • \(\sin(x) \cos(x) = \dfrac{\sin(2x)}{2}\)。
• （积化和差）
  • \(\cos(x) \cos(y) = \dfrac{\cos(x + y) + \cos(x - y)}{2}\)。
  • \(\sin(x) \cos(y) = \dfrac{\sin(x + y) + \sin(x - y)}{2}\)。
  • \(\sin(x) \sin(y) = \dfrac{\cos(x - y) - \cos(x + y)}{2}\)。
• （和差化积）
  • \(\sin(x) + \sin(y) = 2 \sin \left( \dfrac{x + y}{2} \right) \cos \left( \dfrac{x - y}{2} \right)\)。
  • \(\cos(x) + \cos(y) = 2 \cos \left( \dfrac{x + y}{2} \right) \cos \left( \dfrac{x - y}{2} \right)\)。
  • \(\sin(x) + \cos(y) = 2 \sin \left( \dfrac{2x - 2y + \pi}{4} \right) \cos \left( \dfrac{2x + 2y - \pi}{4} \right)\)。

0x06. 向量

定义

1. 模长：向量的长度，\(\vec{a}\) 的模长记作 \(|\vec{a}|\)。

2. 单位向量：模长为 \(1\) 的向量，一般记为 \(\vec{e}\)。

3. 零向量：模长为 \(0\) 的向量，一般记为 \(\vec{0}\)。

定理

1.（共线定理）

• \(\vec{a} \parallel \vec{b}, \vec{b} \neq \vec{0} \iff \exist \lambda, \vec{a} = \lambda \vec{b}\)。
• 点 \(C\) 在直线 \(AB\) 上的充要条件为 \(\forall P, \exist \lambda, \vec{PC} = \lambda \cdot \vec{PA} + (1 - \lambda) \cdot \vec{PB}\)。
  • 若 \(C\) 在线段 \(AB\) 上，则 \(\lambda = \dfrac{BC}{AB}\)。

  证明：点 \(C\) 在直线 \(AB\) 上等价于 \(\exist \lambda, \vec{AC} = \lambda \cdot \vec{AB}\)。

  因为 \(\vec{AC} = \vec{AP} + \vec{PC}, \vec{AB} = \vec{AP} + \vec{PB}\)，所以有：

  \[\begin{aligned} \vec{AP} + \vec{PC} = \lambda \cdot (\vec{AP} + \vec{PB}) &\iff \vec{PC} = \lambda \cdot (\vec{AP} + \vec{PB}) - \vec{AP} \\ &\iff \vec{PC} = (\lambda - 1) \cdot \vec{AP} + \lambda \cdot \vec{PB} \\ &\iff \vec{PC} = (1 - \lambda) \cdot \vec{PA} + \lambda \cdot \vec{PB} \end{aligned} \]

  设 \(\lambda' = 1 - \lambda\)，则 \(\vec{PC} = \lambda' \cdot \vec{PA} + (1 - \lambda') \cdot \vec{PB}\)。证毕。

2.（点乘的几何意义）\(\vec{a} \cdot \vec{b}\) 是 \(\vec{a}\) 在 \(\vec{b}\) 上投影的数量。

3.（夹角公式）设 \(\vec{a}\) 和 \(\vec{b}\) 的夹角为 \(\theta\)，则 \(\cos(\theta) = \dfrac{\vec{a} \cdot \vec{b}}{|\vec{a}| |\vec{b}|}\)。

3.1. 设 \(\vec{a}\) 与 \(\vec{b}\) 的夹角为 \(\theta \in [0, \pi]\)，则有：

• \(\theta < \pi / 2 \iff \vec{a} \cdot \vec{b} > 0\)。
• \(\theta = \pi / 2 \iff \vec{a} \cdot \vec{b} = 0\)。
• \(\theta > \pi / 2 \iff \vec{a} \cdot \vec{b} < 0\)。

4.（点乘的性质）

• （交换律）\(\vec{a} \cdot \vec{b} = \vec{b} \cdot \vec{a}\)。
• （分配律）\(\vec{a} \cdot (\vec{b} + \vec{c}) = \vec{a} \cdot \vec{b} + \vec{a} \cdot \vec{c}\)，\((\vec{a} + \vec{b}) \cdot \vec{c} = \vec{a} \cdot \vec{c} + \vec{b} \cdot \vec{c}\)。

5. \(|\vec{a}| = \sqrt{\vec{a}^2}\)。

6. 设 \(\vec{a} = (x_1, y_1), \vec{b} = (x_2, y_2)\)，则 \(\vec{a} \cdot \vec{b} = x_1 x_2 + y_1 y_2\)。

证明 1 ^[5]：考虑将 \(\vec{a}\) 投影到 \(\vec{b}\) 上。

• \(|\vec{b}| = 1\)：此时 \(\vec{a} \cdot \vec{b}\) 就是投影的数量。

  注意到投影是线性变换，所以考虑求出矩阵 \(M\)，使得 \(M \vec{a}\) 为投影的数量。

  因为 \(\vec{i}\) 在 \(\vec{b}\) 上投影的数量为 \(x_2\)，\(\vec{j}\) 在 \(\vec{b}\) 上投影的数量为 \(y_2\)，所以：

  \[M = \begin{bmatrix} x_2 & y_2 \end{bmatrix} \]

  所以此时 \(\vec{a} \cdot \vec{b} = M \vec{a} = x_1 x_2 + y_1 y_2\)。

• \(|\vec{b}| \neq 1\)：设 \(\vec{b} = \lambda \vec{e} = (\lambda x_2', \lambda y_2')\)，此时 \(\vec{a} \cdot \vec{b}\) 是投影的数量乘 \(\lambda\)。

  则 \(\vec{a} \cdot \vec{b} = \lambda x_1 x_2' + \lambda y_1 y_2' = x_1 x_2 + y_1 y_2\)。

证明 2：

\[\begin{aligned} \vec{a} \cdot \vec{b} &= \left( x_1 \vec{i} + y_1 \vec{j} \right) \left( x_2 \vec{i} + y_2 \vec{j} \right) \\ &= x_1 x_2 \vec{i}^2 + x_1 y_2 \vec{i} \cdot \vec{j} + y_1 x_2 \vec{j} \cdot \vec{i} + y_1 y_2 \vec{j}^2 \\ &\xlongequal{\vec{i} \cdot \vec{j} = 0} x_1 x_2 + y_1 y_2 \end{aligned} \]

7.（三角形的面积公式）设 \(\vec{AB} = (x_1, y_1), \vec{AC} = (x_2, y_2)\)，则 \(S_{\triangle ABC} = \dfrac{1}{2} |x_1 y_2 - x_2 y_1|\)。

---

1. S 指边相等（Side），A 指角相等（Angle）；一般我们按顺时针或逆时针依次寻找三个字母所表示的相等关系。 ↩︎

2. 来自 ProofWiki。 ↩︎

3. 来自百度百科。 ↩︎

4. 来自 ProofWiki。 ↩︎

5. 来自 3Blue1Brown。 ↩︎