三角形的五心

内容暂时不齐，但是笔者也没多少时间，见谅。

记号约定：

• 若角前面没加 \(\angle\) 且无特殊说明，则表示该点上最大的 \(\le 180 \degree\) 的角。
• 对于三角形，使用小写字母表示对应大写字母的顶点所对的边的长度。
  • 例：在 \(\triangle ABC\) 中，\(a\) 表示点 \(A\) 所对的边的边长，即 \(BC\)。
• \(\square\)：证毕。
• \(C_{\omega}\)：\(\omega\) 的周长。

1. 外心（\(O\)）

1.1 基础性质

\(O\) 是三角形 \(\triangle ABC\) 的外接圆的圆心，故有 \(OA = OB = OC\)。

因为 \(OA = OB\)，所以 \(O\) 在 \(AB\) 的中垂线上。同理，\(O\) 也在 \(BC, CA\) 的中垂线上。

把外接圆画出来，可以发现：

\[\begin{aligned} \angle AOB &= 2C \\ \angle BOC &= 2A \\ \angle COA &= 2B \\ \end{aligned} \]

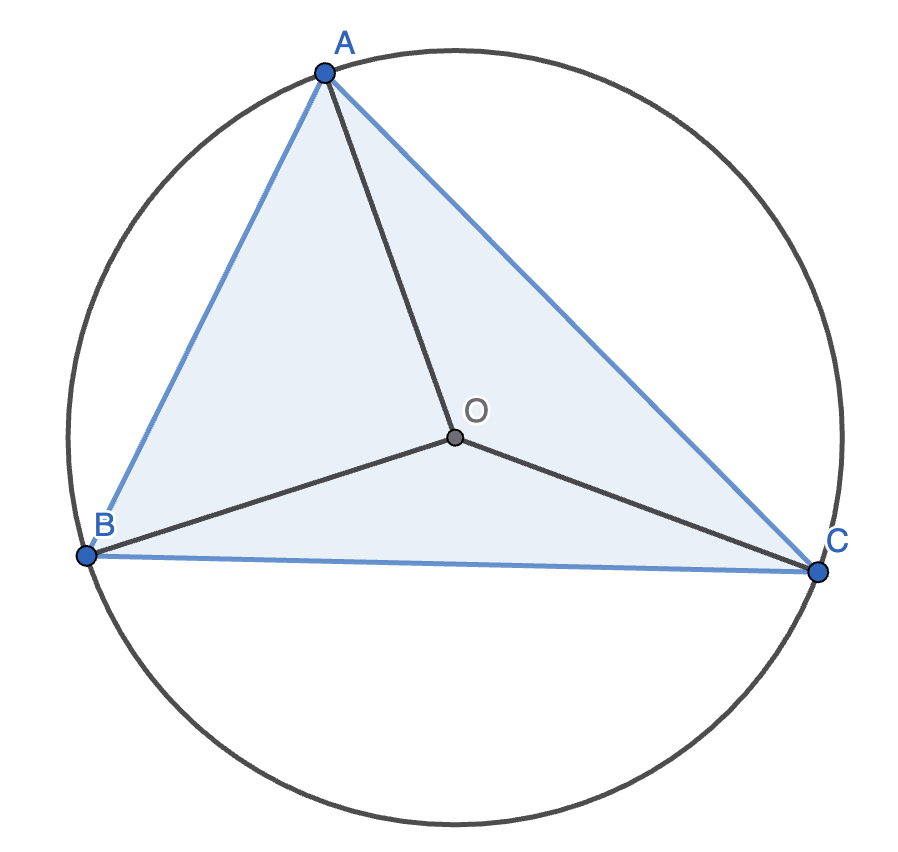
1.2 外接圆的半径

我们考虑求外接圆的半径 \(R\)。从面积入手：

\[2S_{\triangle ABC} = 4R^2 \sin(A) \sin(B) \sin(C) \]

如果再乘一个 \(2R\) 就凑齐 \(abc\) 了！所以：

\[4R \cdot S_{\triangle ABC} = abc \]

即：

\[R = \dfrac{abc}{4S_{\triangle ABC}} \]

2. 重心（\(G\)）

2.1 基础性质

由 Ceva 定理知，\(\triangle ABC\) 三条中线一定交于点 \(G\)。

如图，把 \(\triangle ABC\) 分成 \(6\) 块小三角形，面积分别为 \(S_1, S_2, \cdots, S_6\)。

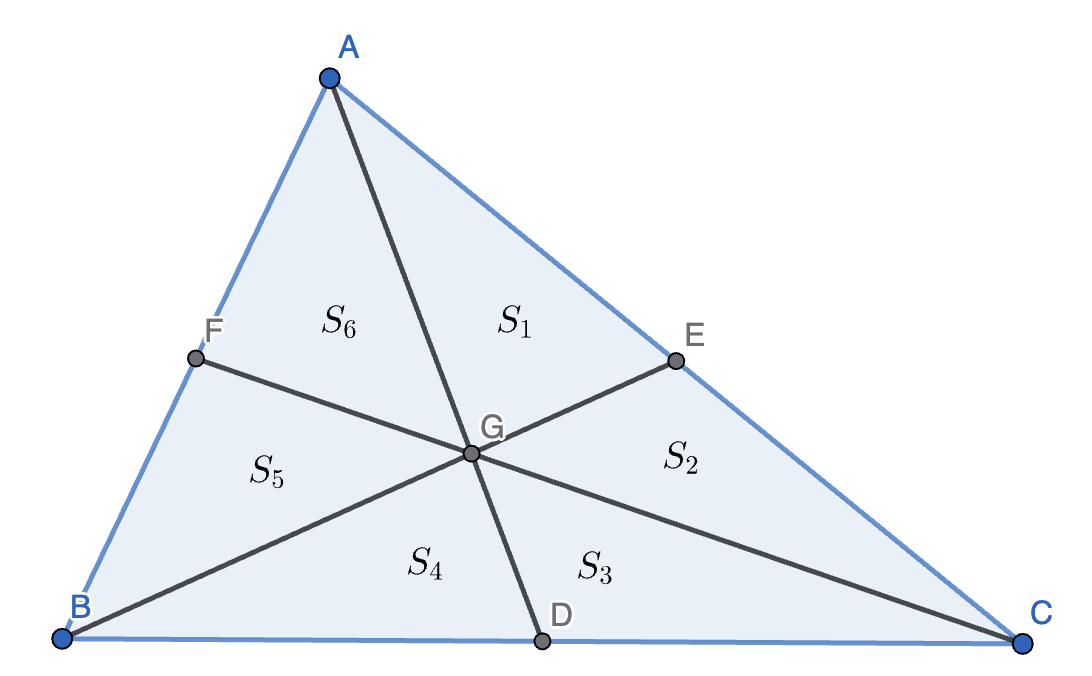
因为 \(BD = CD\)，所以：

\[\begin{align} S_1 + S_2 + S_3 &= S_4 + S_5 + S_6 \\ S_3 &= S_4 \end{align} \]

\((1) - (2)\) 得 \(S_1 + S_2 = S_5 + S_6\)。又因为 \(AE = CE, AF = BF\)，所以 \(S_1 = S_2, S_5 = S_6\)，则 \(S_1 = S_2 = S_5 = S_6\)。

同理得 \(S_1 = S_2 = S_3 = S_4\)，则 \(S_1 = S_2 = S_3 = S_4 = S_5 = S_6\)，则 \(\dfrac{AG}{DG} = \dfrac{BG}{EG} = \dfrac{CG}{FG} = 2\)。

根据上述结论，我们发现这张图有点像三力平衡，于是猜测 \(\overrightarrow{AG} + \overrightarrow{BG} + \overrightarrow{CG} = \mathbf{0}\)。证明不困难，把二力合成的平行四边形画出来，结合中点的条件即可。

于是在平面直角坐标系中，\(G = \left( \dfrac{x_A + x_B + x_C}{3}, \dfrac{y_A + y_B + y_C}{3} \right)\)。

2.2 中线长定理

考虑求中线的长度，以 \(AD\) 为例。我们尝试利用 \(\angle ADB + \angle ADC = 180 \degree\) 的条件：\(\cos(\angle ADC) = \cos(180 \degree - \angle ADB) = -\cos(\angle ADB)\)。

由余弦定理：

\[\begin{align} \cos(\angle ADC) &= \dfrac{AD^2 + CD^2 - AC^2}{2AD \cdot CD} \\ \cos(\angle ADB) &= \dfrac{AD^2 + BD^2 - AB^2}{2AD \cdot BD} \end{align} \]

\((3) + (4)\) 得：

\[\dfrac{AD^2 + BD^2 - AB^2}{2AD \cdot BD} + \dfrac{AD^2 + CD^2 - AC^2}{2AD \cdot CD} = 0 \]

代入 \(BD = CD = \dfrac{BC}{2}\)：

\[\dfrac{AD^2 + \frac{1}{4} BC^2 - AB^2}{AD \cdot BC} + \dfrac{AD^2 + \frac{1}{4} BC^2 - AC^2}{AD \cdot BC} = 0 \]

即：

\[2AD^2 + \dfrac{1}{2} BC^2 - AB^2 - AC^2 = 0 \]

移项得：

\[AD^2 = \dfrac{2(AB^2 + AC^2) - BC^2}{4} = \dfrac{2(b^2 + c^2) - a^2}{4} \]

其它中线同理。

2.3 最值

Fermat 求出了当 \(AP + BP + CP\) 最小时 \(P\) 的位置，我们更进一步，考虑求出当 \(AP^2 + BP^2 + CP^2\) 最小时 \(P\) 的位置。

首先我们求 \(AP^2 + BP^2 + CP^2\) 的表达式。我们知道：

\[\begin{aligned} \overrightarrow{AP} &= \overrightarrow{GP} - \overrightarrow{GA} \\ \overrightarrow{BP} &= \overrightarrow{GP} - \overrightarrow{GB} \\ \overrightarrow{CP} &= \overrightarrow{GP} - \overrightarrow{GC} \end{aligned} \]

于是：

\[\begin{aligned} AP^2 + BP^2 + CP^2 &= \left( \overrightarrow{AP} \right)^2 + \left( \overrightarrow{BP} \right)^2 + \left( \overrightarrow{CP} \right)^2 \\ &= \left( \overrightarrow{GP} - \overrightarrow{GA} \right)^2 + \left( \overrightarrow{GP} - \overrightarrow{GB} \right)^2 + \left( \overrightarrow{GP} - \overrightarrow{GC} \right)^2 \\ &= \left( \overrightarrow{GA} \right)^2 + \left( \overrightarrow{GB} \right)^2 + \left( \overrightarrow{GC} \right)^2 + 3 \left( \overrightarrow{GP} \right)^2 + 2 \overrightarrow{GP} \left( \overrightarrow{GA} + \overrightarrow{GB} + \overrightarrow{GC} \right) \\ &= \left( \overrightarrow{GA} \right)^2 + \left( \overrightarrow{GB} \right)^2 + \left( \overrightarrow{GC} \right)^2 + 3 \left( \overrightarrow{GP} \right)^2 \\ &= AG^2 + BG^2 + CG^2 + 3PG^2 \end{aligned} \]

注意到 \(AG^2 + BG^2 + CG^2\) 为定值，则当 \(P = G\) 时 \(AP^2 + BP^2 + CP^2\) 最小。

2.4 等量关系

\(\overrightarrow{GA} + \overrightarrow{GB} + \overrightarrow{GC} = \mathbf{0}\) 是很好用的等量关系。从这里入手，我们知道：

\[\begin{aligned} \overrightarrow{AB} &= \overrightarrow{GB} - \overrightarrow{GA} \\ \overrightarrow{BC} &= \overrightarrow{GC} - \overrightarrow{GB} \\ \overrightarrow{CA} &= \overrightarrow{GA} - \overrightarrow{GC} \end{aligned} \]

则：

\[\begin{aligned} \left( \overrightarrow{AB} \right)^2 + \left( \overrightarrow{BC} \right)^2 + \left( \overrightarrow{CA} \right)^2 &= \left( \overrightarrow{GB} - \overrightarrow{GA} \right)^2 + \left( \overrightarrow{GC} - \overrightarrow{GB} \right)^2 + \left( \overrightarrow{GA} - \overrightarrow{GC} \right)^2 \\ &= 2 \left( \overrightarrow{GA} \right)^2 + 2 \left( \overrightarrow{GB} \right)^2 + 2 \left( \overrightarrow{GC} \right)^2 - 2 \overrightarrow{GA} \cdot \overrightarrow{GB} - 2 \overrightarrow{GB} \cdot \overrightarrow{GC} - 2 \overrightarrow{GC} \cdot \overrightarrow{GA} \\ &= -\left( \overrightarrow{GA} + \overrightarrow{GB} + \overrightarrow{GC} \right)^2 - 3 \left( \overrightarrow{GA} \right)^2 - 3 \left( \overrightarrow{GB} \right)^2 - 3 \left( \overrightarrow{GC} \right)^2 \\ &= - 3 \left( \overrightarrow{GA} \right)^2 - 3 \left( \overrightarrow{GB} \right)^2 - 3 \left( \overrightarrow{GC} \right)^2 \end{aligned} \]

整理得：

\[\left( \overrightarrow{GA} \right)^2 + \left( \overrightarrow{GB} \right)^2 + \left( \overrightarrow{GC} \right)^2 = \dfrac{\left( \overrightarrow{AB} \right)^2 + \left( \overrightarrow{BC} \right)^2 + \left( \overrightarrow{CA} \right)^2}{3} \]

即：

\[GA^2 + GB^2 + GC^2 = \dfrac{AB^2 + BC^2 + CA^2}{3} \]

3. 垂心（\(H\)）

3.1 基础性质

由定义，\(\triangle ABC\) 的三条高交于 \(H\)。

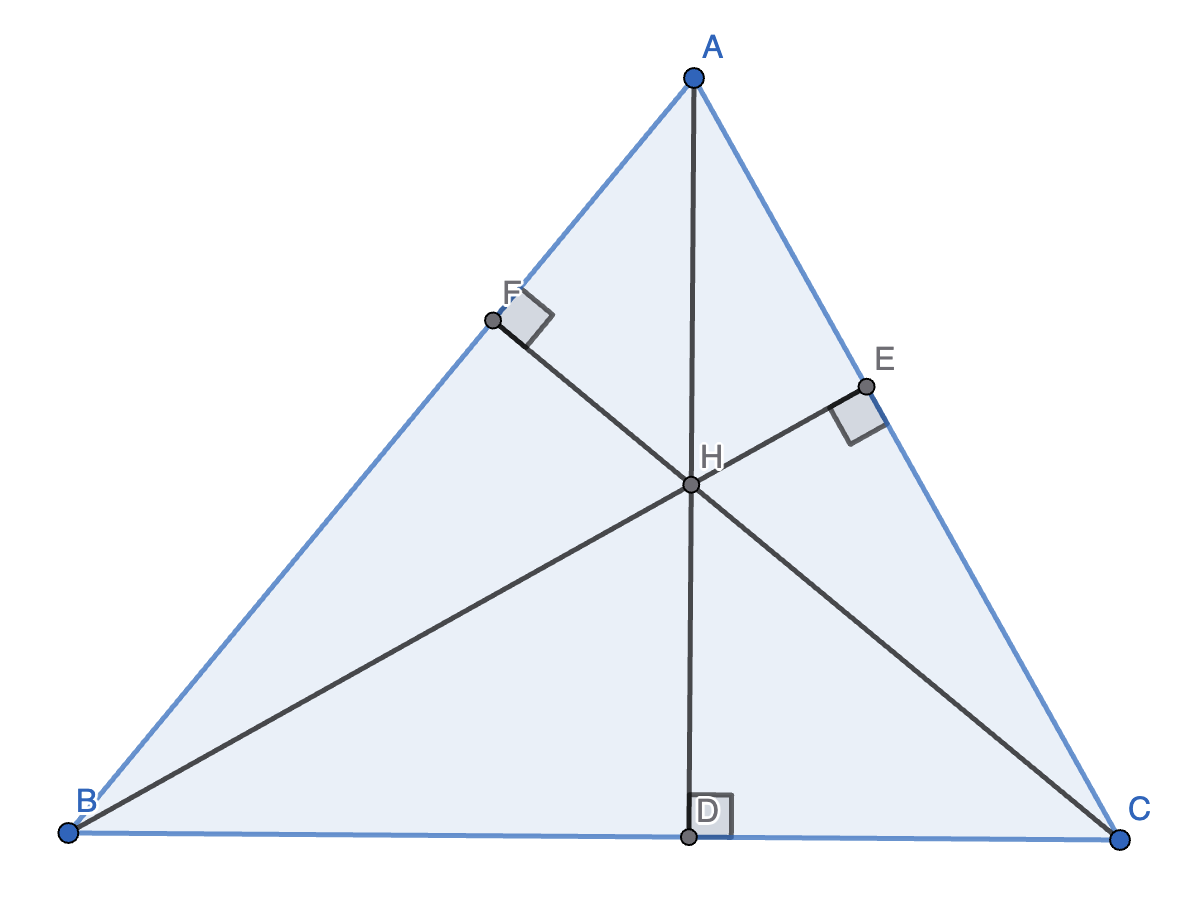
看到相对的直角，要想到四点共圆。容易发现：\((A, E, F, H)\)、\((B, D, F, H)\)、\((C, D, E, H)\)、\((A, B, D, E)\)、\((A, C, D, F)\)、\((B, C, E, F)\) 四点共圆，证明显然。

因为有如此多的四点共圆，所以有关于 \(H\) 的边、角关系很多，导致它很常考。

把 \(6\) 个圆画出来，然后使用圆幂定理可得：

\[\begin{aligned} AH \cdot DH &= BH \cdot EH = CH \cdot FH \\ AF \cdot AB &= AE \cdot AC \\ BD \cdot BC &= BF \cdot BA \\ CE \cdot CA &= CD \cdot CB \\ \end{aligned} \]

3.2 外接圆相关

把外接圆画出来。如果你注意力足够惊人，就可以发现 \(H\) 关于 \(BC\) 的对称点 \(H'\) 在外接圆上。

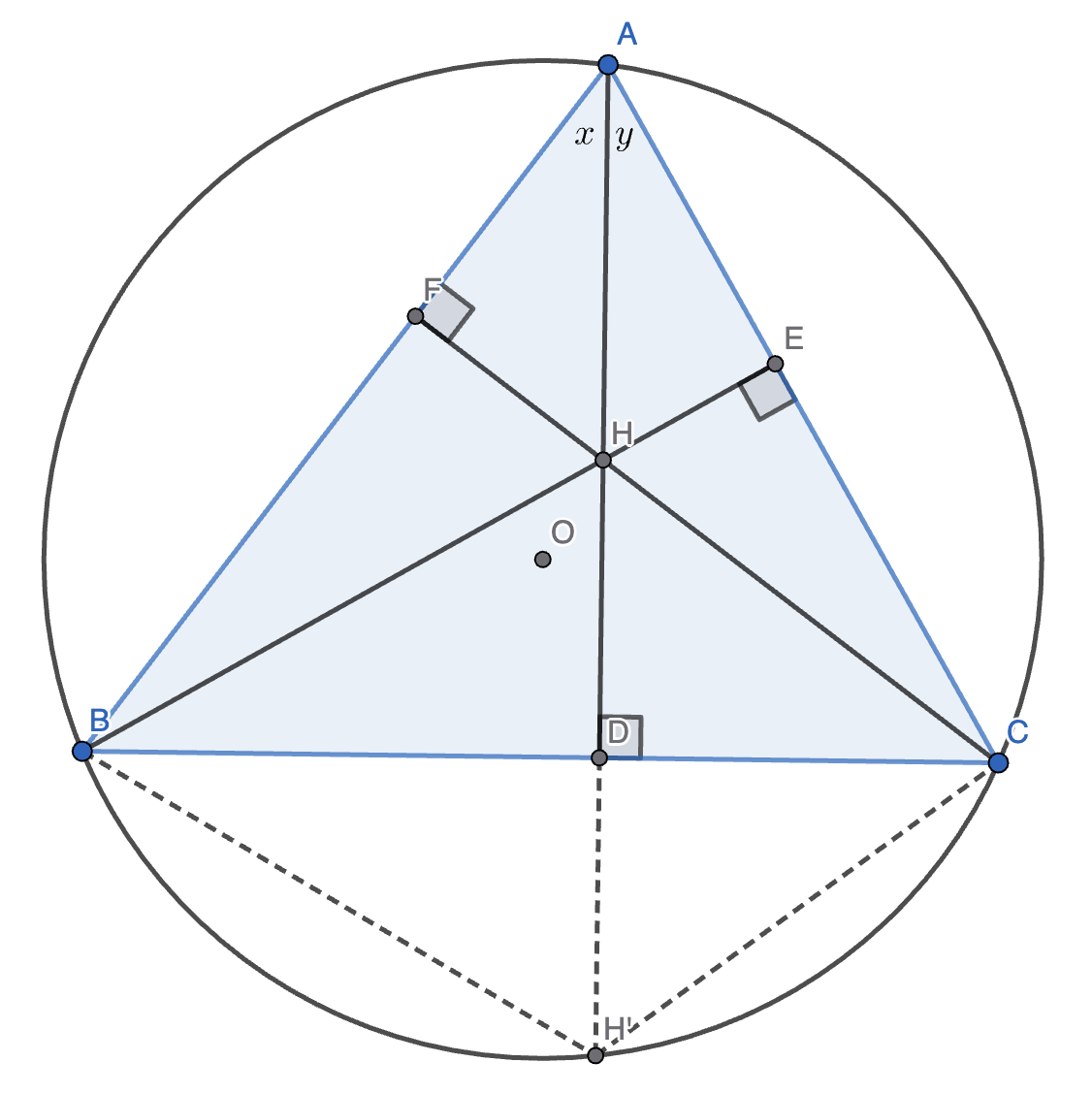
证明：设 \(\angle BAD = x, \angle CAD = y\)，则 \(\angle CHH' = \angle AHF = 90 \degree - x, \angle BHH' = \angle AHE = 90 \degree - y\)。

则 \(\angle BHC = \angle BHH' + \angle CHH' = 180 \degree - x - y = 180 \degree - A\)，所以 \(A, B, C, H'\) 四点共圆。\(\square\)

上图中 \(O\) 没有连边，我们连接 \(AO\) 交外接圆于 \(G\)。

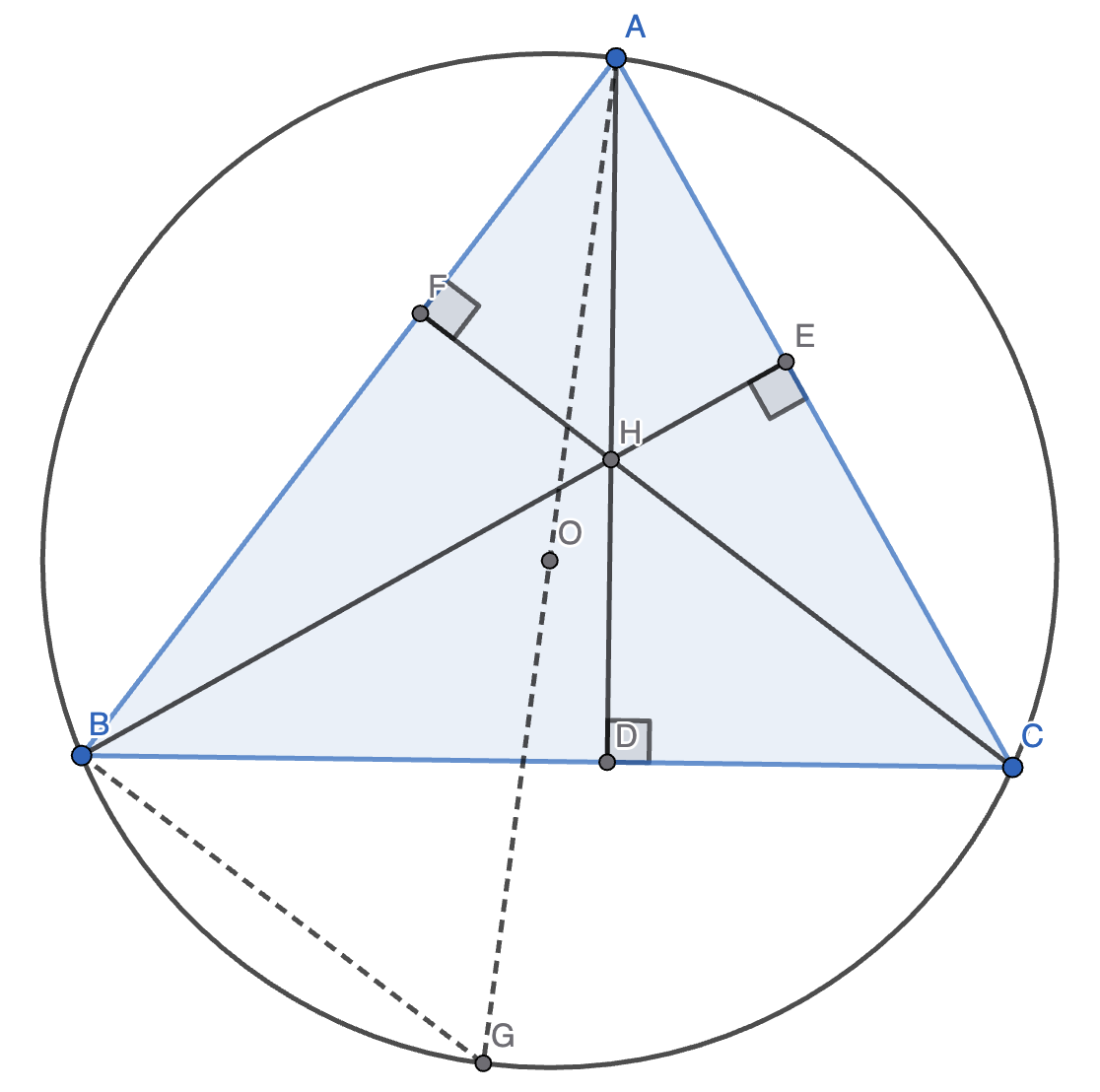
由圆周角定理，\(C = G\)。又因为 \(AG\) 是直径，所以 \(\angle ABG = 90 \degree = \angle ADC\)，所以 \(\triangle ABG \sim \triangle ADC\)，则 \(\angle BAO = \angle CAD\)。

同理有 \(\angle CAO = \angle BAH, \angle BCO = \angle ACH\)。

3.3 欧拉线

\(\triangle ABC\) 的 \(H, O, G\) 共线，且有 \(OH = 3OG\)。

证明：设 \(\mathbf{a} = \overrightarrow{OA}, \mathbf{b} = \overrightarrow{OB}, \mathbf{c} = \overrightarrow{OC}\)，则 \(\overrightarrow{OG} = \mathbf{g} = \dfrac{\mathbf{a} + \mathbf{b} + \mathbf{c}}{3}\)。

现在搞 \(H\)。\(H\) 的性质是 \(AH \perp BC, BH \perp AC, CH \perp AB\)，即：

\[\begin{align} \overrightarrow{AH} \cdot \overrightarrow{BC} = \overrightarrow{BH} \cdot \overrightarrow{AC} = \overrightarrow{CH} \cdot \overrightarrow{AB} = 0 \end{align} \]

设 \(\overrightarrow{OH} = \mathbf{h}\)，则 \(\overrightarrow{AH} = \mathbf{h} - \mathbf{a}, \overrightarrow{BH} = \mathbf{h} - \mathbf{b}, \overrightarrow{CH} = \mathbf{h} - \mathbf{c}\)。代入 \((5)\) 式：

\[\begin{align} (\mathbf{h} - \mathbf{a})(\mathbf{c} - \mathbf{b}) = (\mathbf{h} - \mathbf{b})(\mathbf{a} - \mathbf{c}) = (\mathbf{h} - \mathbf{c})(\mathbf{b} - \mathbf{a}) = 0 \end{align} \]

发现 \(\mathbf{h} = \mathbf{a} + \mathbf{b} + \mathbf{c}\) 是一个解。而 \(H\) 只有一个，所以它是唯一解。

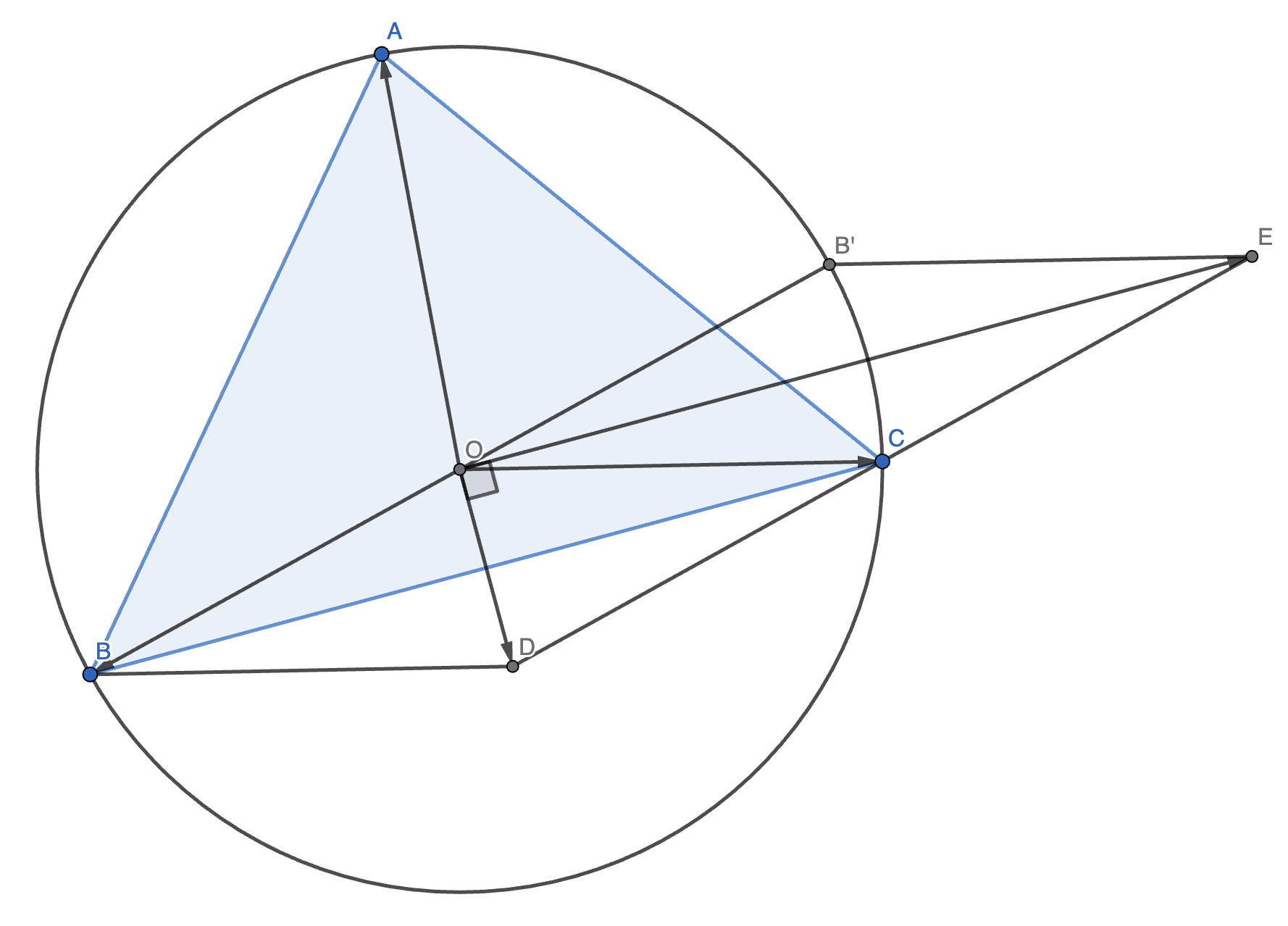
注：为什么它是解？把 \(\mathbf{h} = \mathbf{a} + \mathbf{b} + \mathbf{c}\) 代入，则 \((\mathbf{h} - \mathbf{a})(\mathbf{c} - \mathbf{b}) = (\mathbf{c} + \mathbf{b})(\mathbf{c} - \mathbf{b})\)。

如图，\(\mathbf{c} + \mathbf{b} = \overrightarrow{OD}, \mathbf{c} - \mathbf{b} = \overrightarrow{OE}\)。令 \(\overrightarrow{OB'} = -\mathbf{b}\)，因为 \(B, O, B'\) 共线，而 \(OD\) 平分 \(\angle BOC\)，\(OE\) 平分 \(\angle B'OC\)，则 \(\angle DOE = 90 \degree\)，则 \((\mathbf{c} + \mathbf{b})(\mathbf{c} - \mathbf{b}) = 0\)。剩下的同理。

则 \(\mathbf{h} = 3 \mathbf{g}\)，即 \(\overrightarrow{OH} = 3 \overrightarrow{OG}\)，则 \(H, O, G\) 共线，且 \(OH = 3OG\)。\(\square\)

3.4 线段的长度关系

其实上图给予了更多信息。因为 \(\mathbf{h} = \mathbf{a} + \mathbf{b} + \mathbf{c}\)，所以 \(\overrightarrow{AH} = \mathbf{h} - \mathbf{a} = \mathbf{b} + \mathbf{c}\)，那不就是 \(\overrightarrow{OD}\) 吗？

于是，我们只需求 \(OD\) 即可。这比较好办，因为 \(OD\) 在平行四边形 \(BOCD\) 中。

由圆周角定理，\(\angle BOC = 2A\)，则 \(\angle BOD = \angle COD = A\)。设 \(OB = OC = R\)，则 \(OD = 2R \cos(A) = \dfrac{a}{\sin(A)} \cdot \cos(A) = \dfrac{a}{\tan(A)}\)。

则 \(AH = OD = \dfrac{a}{\tan(A)}\)。其它的同理。

3.4 冷门结论

在 \(\triangle ABC\) 中，设 \(M\) 平分 \(BC\)，\(MH\) 交外接圆于 \(Q\)，则 \(\angle AQM = 90 \degree\)。

证明：如图，作 \(H'\) 为 \(H\) 关于 \(D\) 的对称点，\(H''\) 为 \(H\) 关于 \(M\) 的对称点，则 \(2DM = H'H''\)。

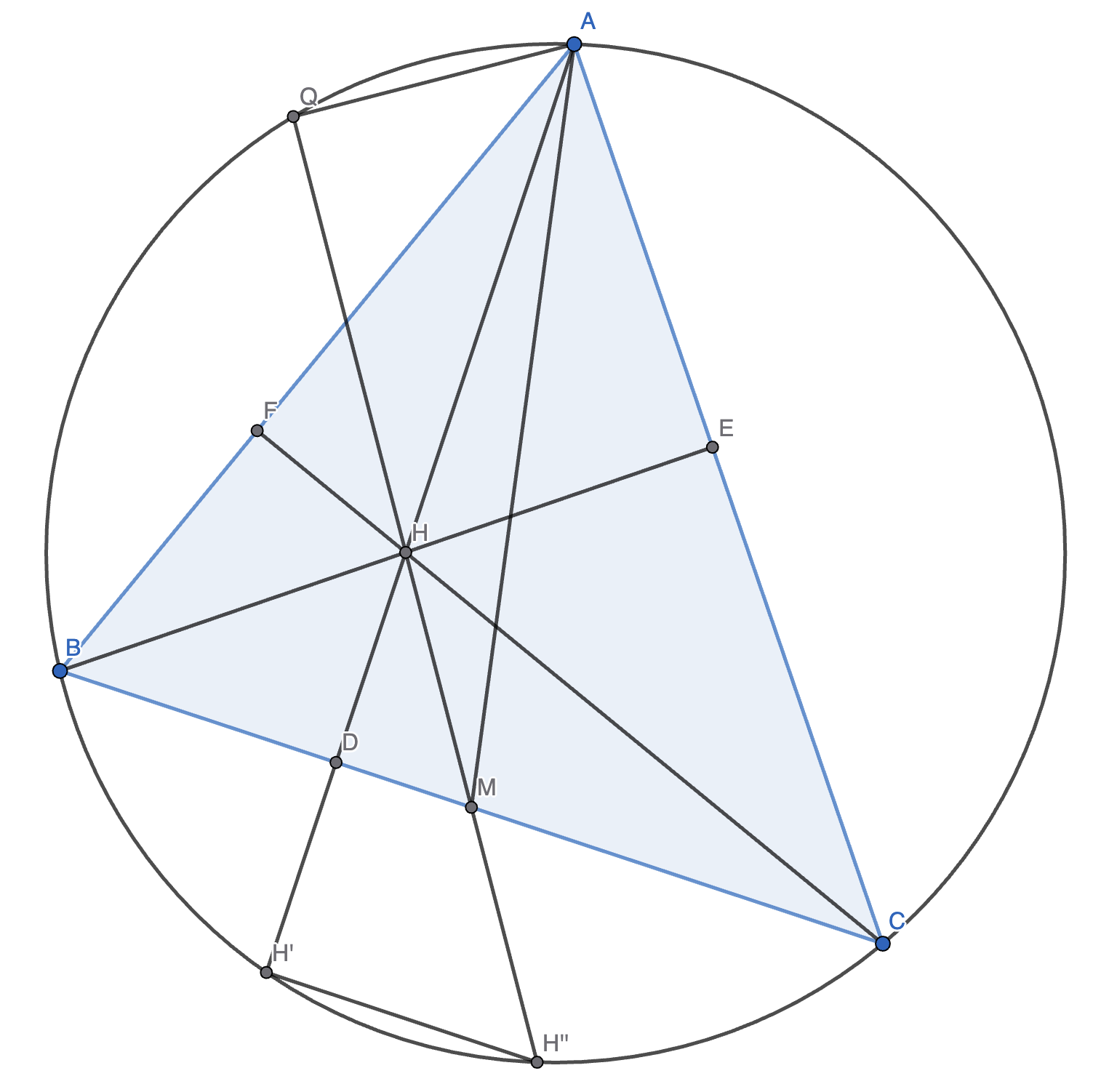
因为 \(\angle HDM = H' = 90 \degree\)，所以 \(M\) 在 \(H'H''\) 的中垂线上。

因为 \(OM \perp BC\)，所以 \(OM\) 是 \(H'H''\) 的中垂线，所以 \(H''\) 在外接圆上。

则由相交弦定理，\(AH \cdot HH' = QH \cdot HH''\)，则 \(\triangle AHQ \sim \triangle H''HH'\)，则 \(\angle AQH = H' = 90 \degree\)。\(\square\)

4. 内心（\(I\)）

4.1 基础性质

由定义，\(\triangle ABC\) 的三条角平分线交于 \(I\)。

设 \(ID \perp a, IE \perp b, IF \perp c\)，则由角平分线定理，\(ID = IE = IF\)。

则 \(I\) 为 \(\triangle ABC\) 内切圆的圆心，\(D, E, F\) 为切点。

导角得：

\[\begin{aligned} \angle AIB &= 90 \degree + \dfrac{C}{2} \\ \angle BIC &= 90 \degree + \dfrac{A}{2} \\ \angle CIA &= 90 \degree + \dfrac{B}{2} \end{aligned} \]

4.2 内切圆半径

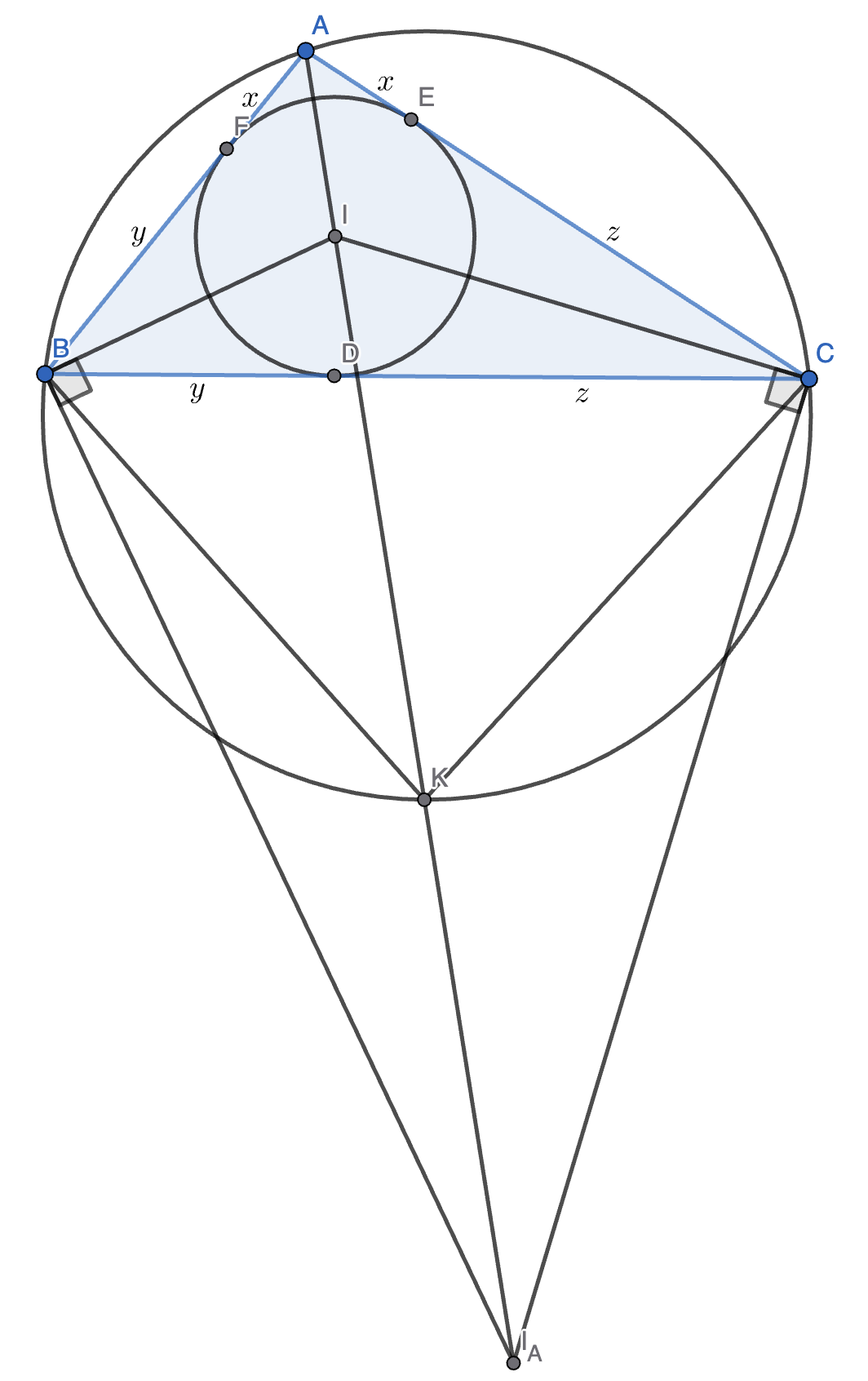
如图，我们尝试求 \(AF\)。

注意到，\(AF = x = (x + y + z) - (y + z) = \dfrac{C_{\triangle ABC}}{2} - a\)。

接下来尝试求 \(ID = IE = IF = r\)。连接 \(ID, IE, IF\)，发现 \(S_{\triangle AIB} + S_{\triangle BIC} + S_{\triangle CIA} = S_{\triangle ABC}\)，则：

\[r = \dfrac{2S_{\triangle ABC}}{a + b + c} \]

观察上图，我们猜测 \(KB = KC = KI = KI_A\)，其中 \(I_A\) 是 \(\triangle ABC\) 的旁心。

证明：因为 \(\angle IBI_A = \triangle ICI_A = 90 \degree\)，所以 \(B, I, C, I_A\) 共圆，圆心为 \(K\)。则 \(KB = KC = KI = KI_A\)。\(\square\)

4.3 线段的长度关系

首先要把内接圆和外接圆画出来，设 \(\odot I\) 切 \(\triangle ABC\) 于 \(D, E, F\)。

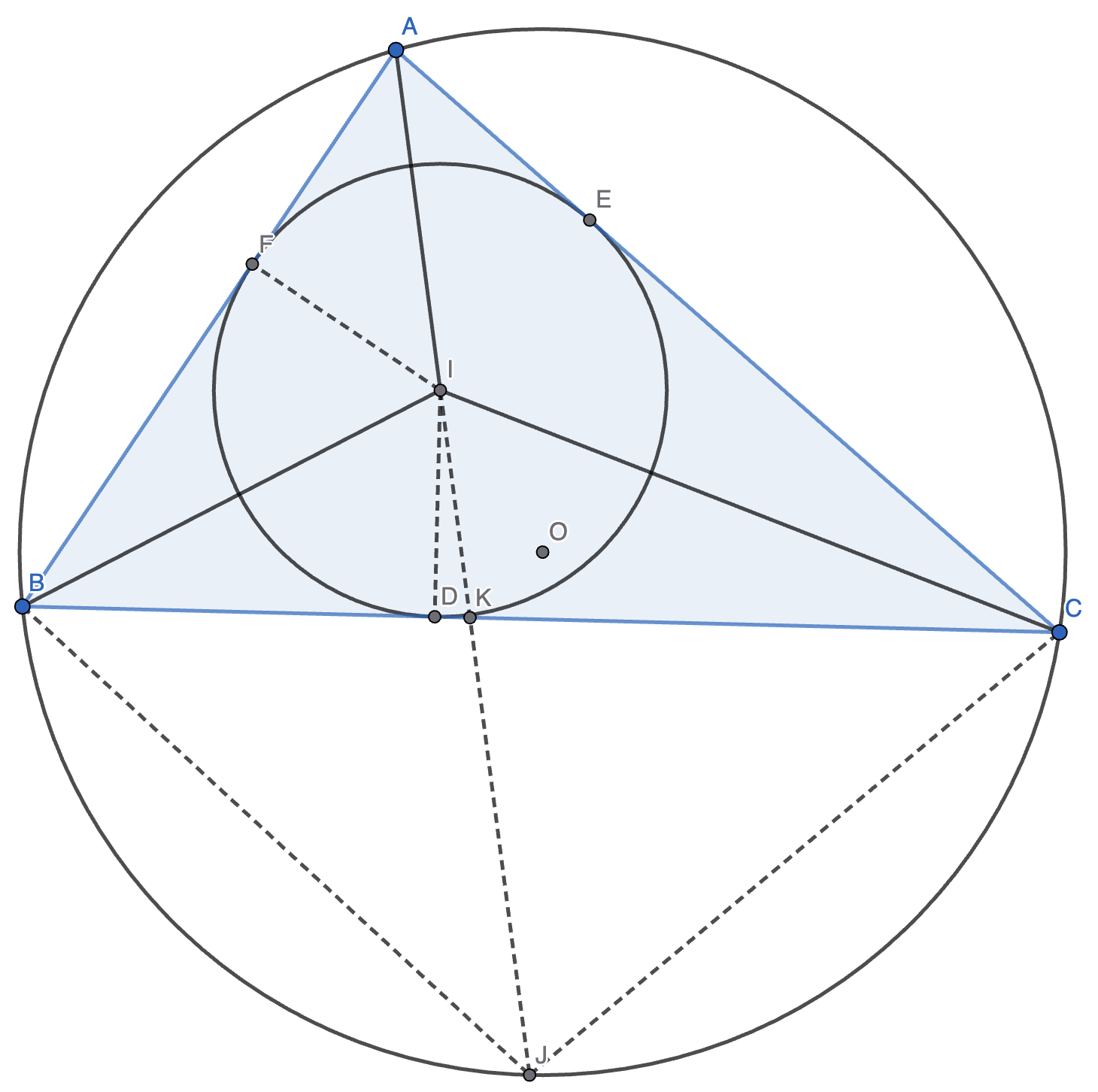
我们发现 \(O\) 是圆心。看到圆心和一点的连线，就可以试一试圆幂定理。

于是延长 \(AI\) 交 \(\odot O\) 于 \(J\)，由圆幂定理得 \(AI \cdot IJ = R^2 - OI^2\)，其中 \(R\) 是 \(\odot O\) 的半径。那我们只用求 \(AI, IJ\) 就可以了。

因为 \(IJ = BJ\)，所以对 \(\triangle ABJ\) 使用正弦定理得 \(IJ = BJ = 2R \sin(A / 2)\)。

然后连接 \(IF\)。因为 \(IF \perp AB\)，所以 \(AI = \dfrac{r}{\sin(A / 2)}\)，其中 \(r = ID = IE = IF\)。

则 \(OI^2 = R^2 - AI \cdot IJ = R^2 - 2R \sin(A / 2) \cdot \dfrac{r}{\sin(A / 2)} = R^2 - 2Rr\)。

设 \(B = \angle ABC, C = \angle ACB\)。

我们接着连接 \(ID\)，发现 \(\angle BID = 90 \degree - \dfrac{B}{2}, \angle BIK = \dfrac{A}{2} + \dfrac{B}{2}\)，则 \(\angle DIK = \angle BIK - \angle BID = 90 \degree - \dfrac{A}{2} - B\)。

又因为 \(ID \perp BC\)，所以 \(KI = \dfrac{r}{\cos(90 \degree - A / 2 - B)} = \dfrac{r}{\sin(A / 2 + B)}\)，所以：

\[\begin{aligned} \dfrac{AI}{KI} &= \dfrac{\sin(A / 2 + B)}{\sin(A / 2)} \\ &= \dfrac{\cos(C / 2 - B / 2)}{\sin(A / 2)} \\ &= \dfrac{\cos(C / 2 - B / 2)}{\cos(C / 2 + B / 2)} \end{aligned} \]

5. 旁心（\(I_A, I_B, I_C\)）

5.1 基础性质

根据定义，在 \(\triangle ABC\) 中，\(I_A\) 是 \(A\) 的内角平分线和 \(B, C\) 的外角平分线的交点。其它的同理。

容易发现，\(I_A, I_B, I_C\) 一定不在 \(\triangle ABC\) 内部。

设 \(I_A D \perp AB, I_A E \perp AC, I_A F \perp BC\)，则 \(I_A D = I_A E = I_A F = r_A\)。以 \(r_A\) 为半径，\(I_A\) 为圆心作圆，则该圆与 \(AB, AC, BC\) 相切。