割点
割点
定义:
若一个点在图中被去掉后,图的连通块个数增加,那么这个点就被称为“割点”。如下图所示红点。
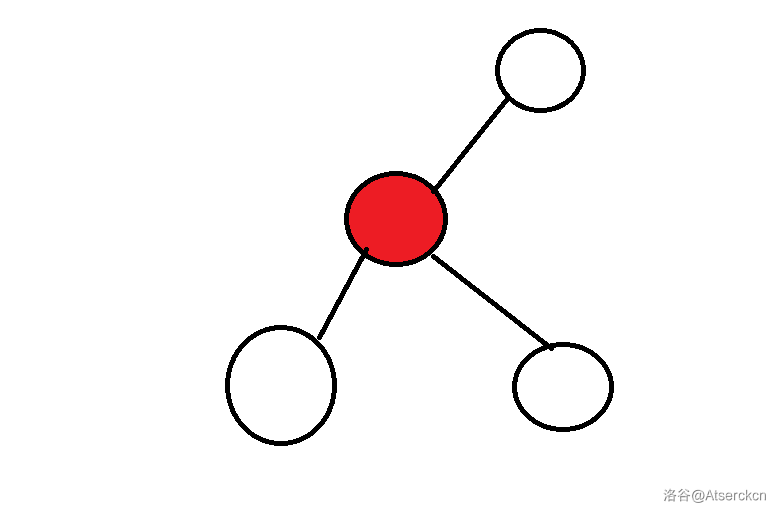
定义说白了就是若去掉一个点,图被“断开”的点称为割点。
朴素算法:
- 枚举每个点 u。
- 遍历图,如果有一个点或多个点遍历不到(遍历期间不能经过点 u),那么 u 就是割点。
时间复杂度:\(O(N^2)\)。
可作为对拍暴力程序。
正解:Tarjan
定义一些东西:
- 时间戳:dfs 时表示每个点被遍历到的“时间”,可用一个不断增加的变量实现。记为 \(dfn\)。
- 搜索树:dfs 时由遍历到的边组成的树(由于有打标记,所以不会重复访问)。
- 追溯值:以 u 为根的子树中,所有不经过 u 能够到达的节点的时间戳的最小值。记为 \(low\)。
关于追溯值:
结合张图来理解:
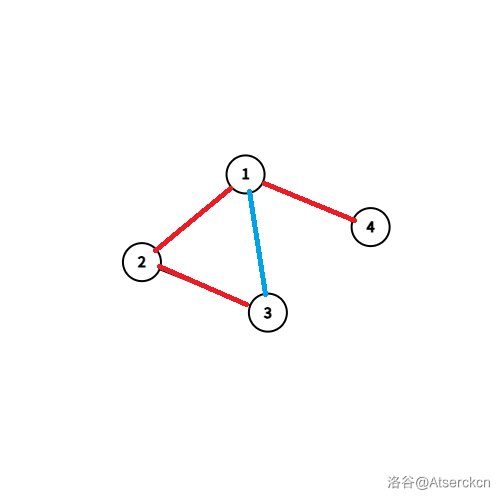
设红边为搜索树的边,则 \(3\) 号点因为有蓝色的边不经过他的父亲 \(2\) 号点,直接到达了 \(1\) 号点,所以 \(low_3=dfn_1\)。
回归 Tarjan
有一个重要的概念:
一个点 u 如果是割点,那么它的子树中的一些节点 v 的 \(low_v\) 是大等于 \(dfn_u\) 的,因为它到不了上面(上面的意思是搜索树中比 u 更早遍历到的点集)。
显然,\(low_u\) 表示假设断开点 u 孩子们还能遍历到的最早时间戳。
若 \(low_v\ge dfn_u\) (v 是 u 的孩子),即 v 回不到 u 前,那么就表示 u 是割点。
有 \(s\) 个这样的 v 就代表断开 u 可以把原先的连通图变成 \(s+1\) 个连通块(u 上方也是一个)。
遍历路上
对于每个点 u,遍历到的儿子 v 有两种可能:
- \(dfn_v=0\)
说明 v 是新加入搜索树中的节点,那么就先递归下去,用 \(low_v\) 更新 \(low_u\)。
即 \(low_u=min(low_u,low_v)\)。
- \(dfn_v\neq 0\)
说明 v 曾经被遍历过,是搜索树上 u 的祖先,那么用 \(dfn_v\) 更新 \(low_u\)。
即 \(low_u=min(low_u,dfn_v)\)。
然而上述办法还是有 bug。想想在哪呢?
发现 bug
假设我们搜索树从 \(1\) 号点开始遍历,给张图你就懂。
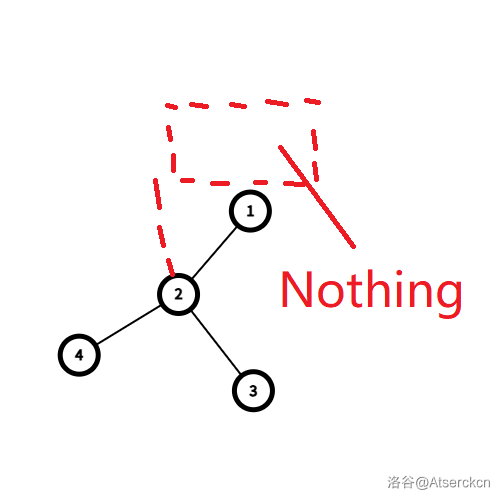
如图。
因为我们是从 \(1\) 号点开始遍历的,\(1\) 号点是搜索树的根,它哪来的祖先能让孩子们去更新追溯值啊!!!
而图中的 \(1\) 号点又显然不是割点。
咋办呢?
解决 bug
特判呗。反正根只有一个。
这时候我们得思考:什么样的情况下根是割点?
反正追溯值做不了了。
那么看看朴素的图吧。
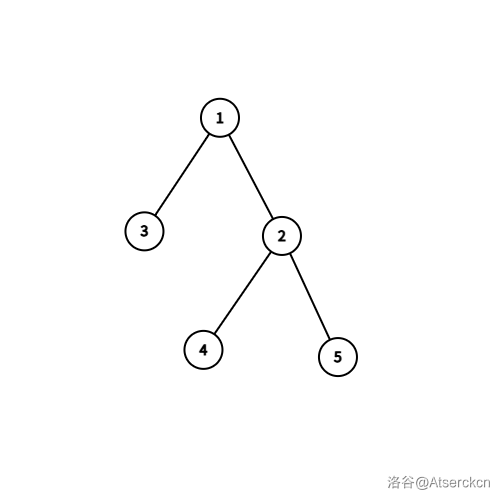
图中 \(1\) 号点就是割点。
为啥嘞?
答:因为把它删了后有两个连通块。
正解。
我们记录一下,如果它在搜索树上的儿子不止一个,那么它就是割点。
就这么简单?
就这么简单。
这时候不知道有没有同学有个疑惑和我初学时一样的,如图:
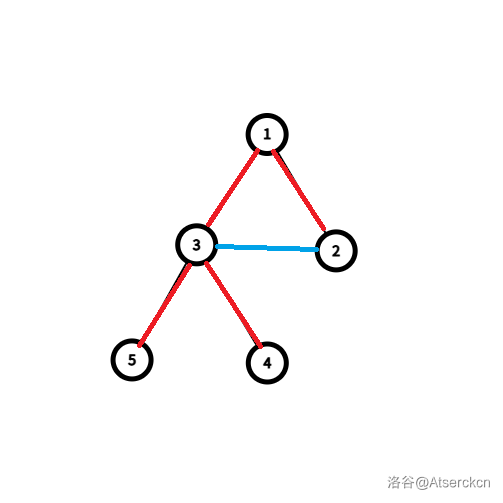
红色的是搜索树边。
图中 \(1\) 不是割点啊,但它在树上还真有两个孩子啊??
如果您一开始没看出来哪儿错了,就点个赞再走吧。
注意到边 \(3\rightarrow 2\) 和 \(1\rightarrow 2\)。
当我们遍历到点 \(3\) 的时候,它就会顺带把 \(2\) 号点先遍历了。先遍历到 \(2\) 再遍历 \(3\) 同理。
所以说搜索树应该为:
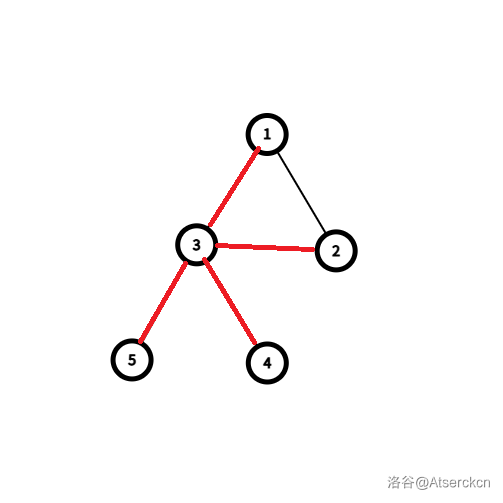
或:

OK,下班,看题。
题意很简略了。就是看看实现。
#include<bits/stdc++.h>
using namespace std;
const int N=2e4+5,M=1e5+5;
int n,m,ehead[N],cnt_e,low[N],dfn[N],idx,rt,cntans;
bool ans[N];//是否为割点
struct E{
int to,pre;
}e[M<<1];
void adde(int from,int to)
{
e[++cnt_e].to=to;
e[cnt_e].pre=ehead[from];
ehead[from]=cnt_e;
return;
}
void dfs(int u)
{
low[u]=dfn[u]=++idx;
int chtree=0;//如果是根的话,它的孩子个数
for(int i=ehead[u];i;i=e[i].pre)
{
int v=e[i].to;
if(!dfn[v])//不在搜索树上
{
dfs(v);
low[u]=min(low[u],low[v]);
if(rt==u)++chtree;
if(low[v]>=dfn[u]&&rt!=u&&(!ans[u]))//注意 (!ans[u])。搞不好会重复算 cntans
{
++cntans;
ans[u]=1;
}
}
else//返祖边
low[u]=min(low[u],dfn[v]);
}
if(u==rt&&chtree>1&&(!ans[u]))
{
++cntans;
ans[u]=1;
}
return;
}
int main(){
ios::sync_with_stdio(0);
cin>>n>>m;
for(int i=1,u,v;i<=m;++i)
{
cin>>u>>v;
adde(u,v);adde(v,u);
}
for(int i=1;i<=n;++i)//图不保证联通
{
if(!dfn[i])
{
rt=i;
dfs(i);
}
}
cout<<cntans<<'\n';
for(int i=1;i<=n;++i)
if(ans[i])
cout<<i<<' ';
cout<<'\n';
return 0;
}
闲话时间
讲个好玩的,这篇文章是我晚上十一点左右写的,但是:
我来自报家门了。
正题。
Tarjan 算法不光能解决割点的问题,改一改还能当作强连通分量和割边(又称桥)和双连通分量等等。
说到强连通分量,推销一下我的学习笔记不过分吧 qwq。
完结撒花。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号