强连通分量

强连通分量

强连通定义

有向图 $G$ 的强连通是指 $G$ 中任意两个节点都可以直接或间接到达。

下方两幅图都是强连通。一个特殊一点，任意两点都可以直接到达；一个则是最常见的强连通图。

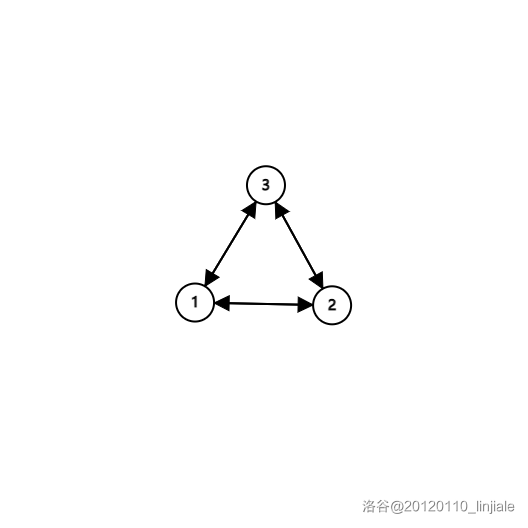
• 特殊强连通图，任意两点都可以直接到达

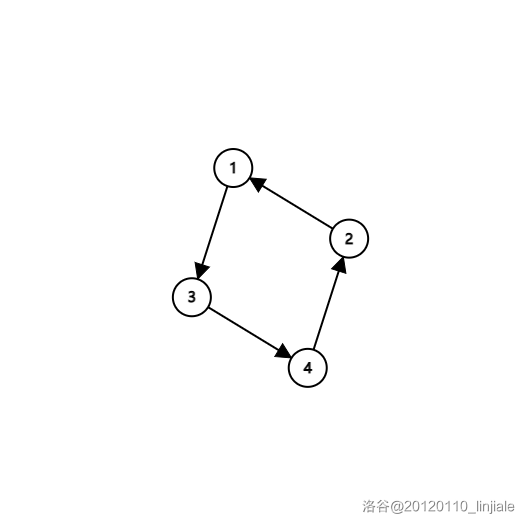
• 常见的强连通图，即一个环

强连通分量

强连通分量，简称 $SCC$，是在一个有向图中极大的强连通子图。

重点：SCC不一定是最大的！

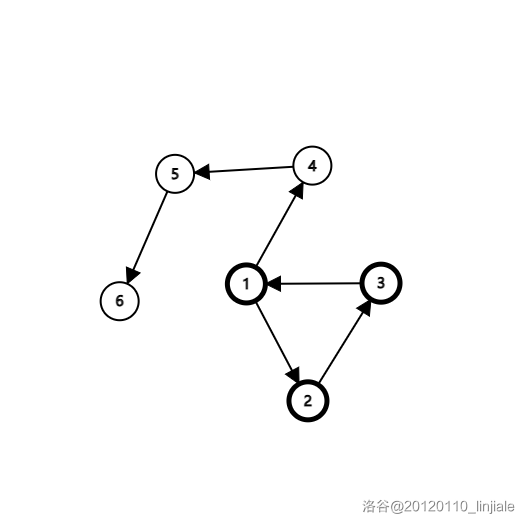
• 图中加粗的点组成的子图即为此图的强连通分量

dfs 生成树的边

dfs 遍历过程就不多说了，这是图论基本能力。

dfs 深搜后，会出现四种不同情况的边，如下：

• 树边：由 dfs 自然搜索到的边，组成一棵树（不一定是最小/大生成树）。
• 返祖边（回边）：由一个节点指向前面已经遍历过的祖先节点的边。
• 横叉边：指向了一个访问过但不是当前节点的祖先的边。
• 前向边：指向了目前未遍历到的节点，但以后会遍历到的节点的边。

例如，下图即为一张图 $G$。

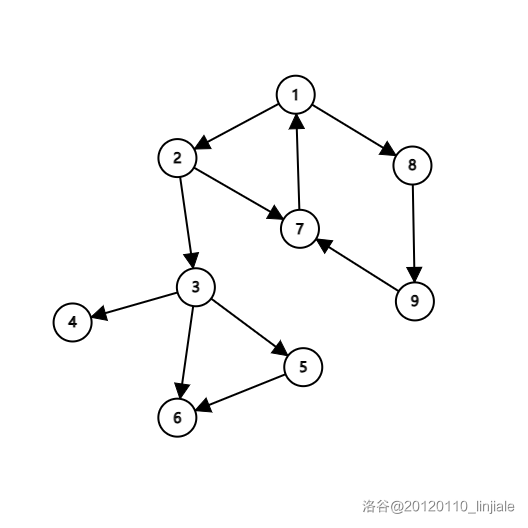
不难看出，dfs 生成树长这样：

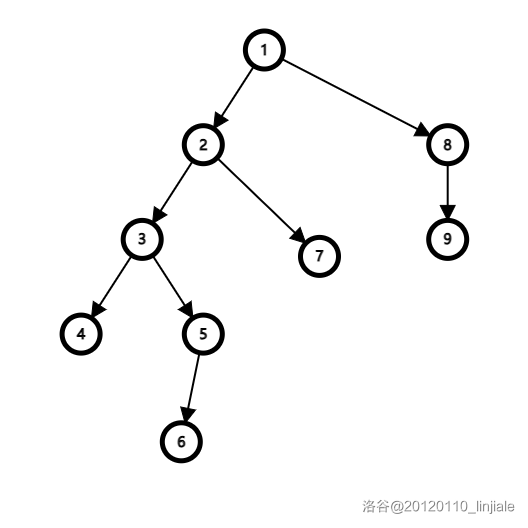
对比一下，如下：

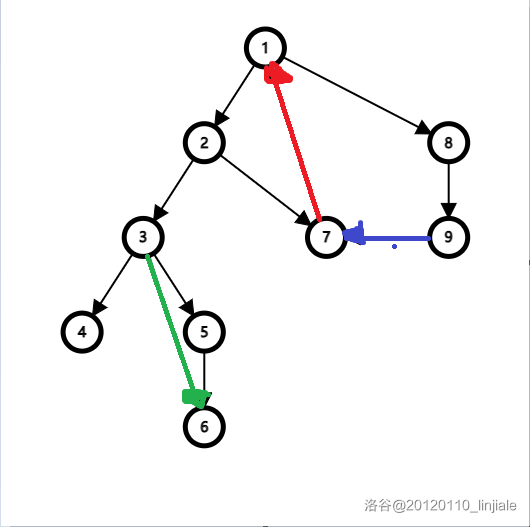
黑边为树边，是正常深搜而来的。

红边即为返祖边，因为它指向了当前节点 $7$ 的祖先。

蓝边即为横叉边，因为它指向了当前生成树的另一个节点，但不是当前节点 $9$ 的祖先。

绿边即为前向边，指向了还未加入生成树的节点。

Tarjan 算法

Tarjan 算法是用来求解 $SCC$ 的著名算法，可以在线性时间复杂度完成统计 $SCC$ 的任务。

思路

若节点 $u$ 是 $SCC$ 在搜索树中访问到的第一个节点，那么 $SCC$ 就肯定是一个以 $u$ 为根节点的子树，我们称 $u$ 为这个 $SCC$ 的根。

Tarjan 算法基本思路为把每个 $SCC$ 都看作搜索树的一个子树，将其节点一个个保存。

对于两个节点 $u$ 和 $v$，若 $u$ 是 $v$ 的祖先，且 $v$ 有一条返祖边能指向 $u$，则 $u$ 和 $v$ 形成了环，属于一个 $SCC$。从 $u$ 到 $v$ 一路上遇到的所有点也属于这一 $SCC$ 中的点，边也为 $SCC$ 中边。

步骤

每次遍历到一个节点 $u$，需要统计一下信息：

• dfn[u]，即 $u$ 的时间戳（第几个被访问到的）。
• low[u]，$u$ 属于的那个 $SCC$ 中 dfn 最小的时间戳。

初始化时，dfn[u]=low[u]=++tot，tot 为时间戳。

既然 dfs 是一种递归的算法，不妨用栈来存节点信息。

每次搜到一个节点都将其入栈，有出度则沿着出度遍历。

上文说到，dfs 搜索会搜到 $4$ 种边，那么我们该如何解决 $4$ 种边呢？

• 树边：正常搜
• 返祖边：更新当前的 low 值
• 横叉边：无视，没用
• 前向边：无视，没用

每次搜完子树都需要更新 $u$ 的 low 值，若 low[u]==dfn[u]，则 $u$ 为这个 $SCC$ 的根节点，因为没有比他时间戳更小的了（回溯完之后）。

例题：福州一中OJ P2110 求有向图的强连通分量

AC Code:

#include<bits/stdc++.h>
using namespace std;
const int MAXN=2e5+5,MAXM=8e5+5;
struct EDGE{
	int to,pre;
}edge[MAXM<<1];
int head[MAXN],cnt_edge,tot,t;
int n,m,op;
//链式前向星存图 
void add(int from,int to)
{
	edge[++cnt_edge].to=to;
	edge[cnt_edge].pre=head[from];
	head[from]=cnt_edge;
	return;
}
int dfn[MAXN],low[MAXN];
stack<int> st;
bool vis[MAXN];
int cnt_ans,cnt_t,maxn;
void dfs(int u)//目标是统计maxn 
{
	dfn[u]=low[u]=++tot;//时间戳和子树最小时间戳 
	st.push(u);
	vis[u]=true;
	for(int i=head[u];i;i=edge[i].pre)
	{
		if(!dfn[edge[i].to])
		{
			dfs(edge[i].to);
			low[u]=min(low[u],low[edge[i].to]);//更新 
		}
		else
			if(vis[edge[i].to])//返祖边，注意是vis，不是dfn(有可能是横叉边) 
				low[u]=min(low[u],dfn[edge[i].to]);
	}
	if(low[u]==dfn[u])//是SCC的根节点 
	{
		cnt_t=0;//统计SCC节点个数 
		do{//记得是先做在判断 
			vis[t=st.top()]=false;//比u后入栈的都是SCC的子节点 
			st.pop();
			cnt_t++;
		}while(u!=t);
		maxn=max(maxn,cnt_t);
	}
	return;
}
void dfs2(int u)//与dfs大同小异，目标是计算有多少个强连通子图 
{
	dfn[u]=low[u]=++tot;
	st.push(u);
	vis[u]=true;
	for(int i=head[u];i;i=edge[i].pre)
	{
		if(!dfn[edge[i].to])
		{
			dfs2(edge[i].to);
			low[u]=min(low[u],low[edge[i].to]);
		}
		else
			if(vis[edge[i].to])
				low[u]=min(low[u],dfn[edge[i].to]);
	}
	if(low[u]==dfn[u])
	{
		cnt_t=0;
		do{
			vis[t=st.top()]=false;
			st.pop();
			cnt_t++;
		}while(u!=t);
		if(cnt_t==maxn)
			cnt_ans++;
	}
	return;
}
int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
	{
		scanf("%d",&op);
		while(op--)
		{
			scanf("%d",&t);
			add(i,t);
		}
	}
	for(int i=1;i<=n;i++)
		if(!dfn[i])
			dfs(i);
	//初始化 
	while(!st.empty())
		st.pop();
	for(int i=1;i<=n;i++)
	{
		dfn[i]=0;
		low[i]=0;
		vis[i]=false;
	}
	//初始化 
	for(int i=1;i<=n;i++)
		if(!dfn[i])
			dfs2(i);
	printf("%d %d\n",maxn,cnt_ans);
	return 0;
}