求解范围中 gcd(a,b)== prime 的有序对数
题目:
给定整数N,求1<=x,y<=N且Gcd(x,y)为素数的
数对(x,y)有多少对.
输入:
一个整数N。
输出:
如题。
Sample Input
4
Sample Output
4
Hint
对于样例(2,2),(2,4),(3,3),(4,2)
1<=N<=10^7
思路:
对于本题,因为是使得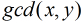
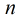
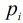
只需要求在区间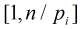
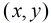
也就是说,现在问题转化为:在区间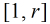
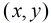
是有序对,不妨设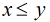
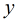
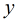
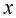
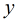
我们可以递推法求欧拉函数,将得到的答案乘以2即可,但是这里乘以2后还有漏计算了的,那么有哪些呢?
是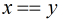
另外,在bzoj上好像空间限制的原因要用埃氏筛法筛质数,而在nyzoj上,数据点较大,最好用欧拉筛筛质数。
//nyzoj(乌市一中在线评测) www.nyzoj.com:5283 题目:blcup (10053)
代码如下:
//bzoj AC版:
#include<cstdio> typedef long long ll; const ll N=1e7+9; ll n,f[N],phi[N]; bool prime[N]; ll p[N],cnt; void prework() { for (int i=2;i<=n;i++) prime[i]=1; for (int i=2;i<=n;i++) { if (prime[i]) { p[++cnt]=i; for (int j=i<<1;j<=n;j+=i) prime[j]=0; } } } void Er() { for (int i=1;i<=n;i++) phi[i]=i; for (int i=2;i<=n;i+=2) phi[i]>>=1; for (int i=3;i<=n;i+=2) { if (phi[i]==i) for (int j=i;j<=n;j+=i) phi[j]=phi[j]-phi[j]/i; } f[1]=0; for (int i=2;i<=n;i++) f[i]=f[i-1]+(phi[i]<<1); } ll solve() { ll ans=0; for (int i=1;i<=cnt;i++) { ans+= 1 + f[n/p[i]] ; } return ans; } int main() { scanf ("%lld",&n); prework(); Er(); printf("%lld",solve()); return 0; }
//nyzoj AC 版:
#include<cstdio> typedef long long ll; const ll N=1e7+7; ll n,f[N],phi[N]; int v[N]; ll p[N],cnt; void prework() { for (int i=2;i<=n;i++) { if (v[i]==0) { v[i]=i; p[++cnt]=i; } for (int j=1;j<=cnt;j++) { if (p[j]>v[i] || p[j]>n/i) break; v[i*p[j]]=p[j]; } } } void Er()//递推求欧拉函数 { for (int i=1;i<=(n>>1);i++) phi[i]=i; for (int i=2;i<=(n>>1);i+=2) phi[i]>>=1; for (int i=3;i<=(n>>1);i+=2) { if (phi[i]==i) for (int j=i;j<=(n>>1);j+=i) phi[j]=phi[j]-phi[j]/i; } f[1]=0; for (int i=2;i<=(n>>1);i++) f[i]=f[i-1]+(phi[i]<<1); } ll solve() { ll ans=0; for (int i=1;i<=cnt;i++) { ans+= 1 + f[n/p[i]] ; } return ans; } int main() { scanf ("%lld",&n); prework(); Er(); printf("%lld",solve()); return 0; }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号