A Concise Introduction to Logic - PART II: FORMAL LOGIC - Chapter 6: Propositional Logic

PART II: FORMAL LOGIC

Chapter 6: Propositional Logic

6.1 Symbols and Translation

Earlier chapters showed that the validity of a deductive argument is purely a function of its form. By knowing the form of an argument, we can often tell immediately whether it is valid or invalid. Unfortunately, however, ordinary linguistic usage often obscures the form of an argument. To dispel this obscurity, logic introduces various simplifying procedures. In Chapter 5, letters were used to represent the terms in a syllogism, and techniques were developed to reduce syllogisms to what is called standard form. In this chapter, form recognition is facilitated through the introduction of special symbols called operators, or connectives. When arguments are expressed in terms of these symbols, determining validity often becomes a matter of mere visual inspection.

In the two previous chapters, the fundamental elements were terms. In propositional logic, however, the fundamental elements are whole statements (or propositions). Statements are represented by letters, and these letters are then combined by means of the operators to form more-complex symbolic representations.

To understand the symbolic representation used in propositional logic, we must distinguish simple statements from compound statements. A simple statement is one that does not contain any other statement as a component. Here are some examples:

Any convenient uppercase letter may be selected to represent each statement. Thus, F might be selected to represent the first, J the second, P the third, and B the fourth. As will be explained shortly, lowercase letters are reserved for use as statement variables.

A compound statement is one that contains at least one simple statement as a component. Here are some examples:

Using letters to stand for the simple statements, these compound statements may be represented as follows:

In the first example, note that the statement is compound even though it contains only a single component (A). In general, negative statements are interpreted as compound units consisting of an affirmative statement and the phrase “it is not the case that.”

The expressions “it is not the case that,” “and,” “or,” “if . . . then . . . ,” and “if and only if” are translated by logical operators. The five logical operators are as follows:

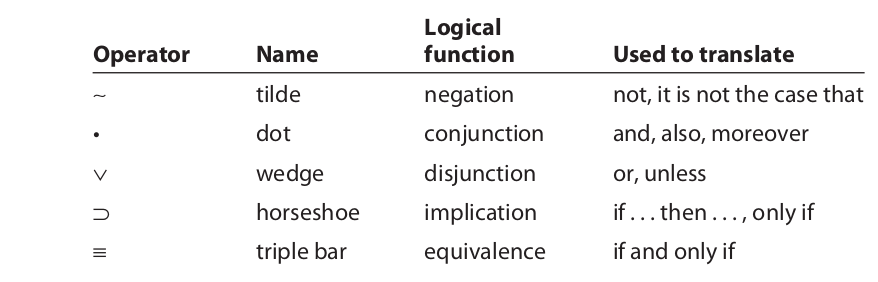
Saying that logical operators are used to “translate” these English expressions does not mean that the expressions and the operators are identical. As in any translation (from English to French, for example), a certain distortion of meaning occurs.

The meaning of such English expressions as “and,” “or,” and “if and only if ” is often vague and may vary with context, whereas the meaning of the logical operators is clear, precise, and invariable. Thus, when we say that the logical operators may be used to translate expressions in ordinary language, we mean that the operators capture a certain aspect of their correlative English expressions. The precise character of this aspect is spelled out in the next section of this chapter. The purpose of this section is to develop a familiarity with the logical operators through practice in translation.

When we use the operators to translate the previous examples of compound statements, the results are as follows:

The statement ∼A is called a negation. The statement D • C is called a conjunctive statement (or a conjunction), and the statement P ∨ E is called a disjunctive statement (or a disjunction); in the conjunctive statement, the components D and C are called conjuncts, and in the disjunctive statement the components P and E are called disjuncts. The statement W ⊃ F is called a conditional statement (or a conditional), and it expresses the relation of material implication. Its components are called antecedent (W) and consequent (F). Lastly, B ≡ R is called a biconditional statement (or a biconditional), and it expresses the relation of material equivalence.

 

At this point we should define what is called the main operator in a compound statement. The main operator is the operator that has as its scope everything else in the statement. If there are no parentheses in the statement, the main operator will either be the only operator or, if there is more than one, it will be the operator that is not a tilde. If there are parentheses, brackets, or braces in the statement, the main operator will be the operator that lies outside all parentheses, brackets, and braces; if there is more than one such operator, the main operator will be the one that is not a tilde.

 

Let us now use the logical operators to translate additional English statements. The tilde symbol is used to translate any negated simple proposition:

 

 

The dot symbol is used to translate such conjunctions as “and,” “also,” “but,” “however,” “yet,” “still,” “moreover,” “although,” and “nevertheless”:

Note that the last example is equivalent in meaning to “Tiffany sells jewelry, and Ben Bridge sells jewelry.” To translate such a statement as a conjunction of two simple statements, the original statement must be equivalent to a compound statement in English. For example, the statement “Mary and Louise are friends” is not equivalent in meaning to “Mary is a friend, and Louise is a friend,” so this statement cannot be translated as M • L.

 

The wedge symbol is used to translate “or” and “unless.” A previous chapter explained that “unless” is equivalent in meaning to “if not.” This equivalence holds in propositional logic as well, but in propositional logic it is usually simpler to equate “unless” with “or.” For example, the statement “You won’t graduate unless you pass freshman English” is equivalent to “Either you pass freshman English or you won’t graduate” and also to “If you don’t pass freshman English, then you won’t graduate.” As the next section demonstrates, the wedge symbol has the meaning of “and/or”—that is, “or” in the inclusive sense. Although “or” and “unless” are sometimes used in an exclusive sense, the wedge is usually used to translate them as well.

The word “either,”which is often used to introduce disjunctive statements, has primarily a punctuational meaning. The placement of this word often tells us where parentheses and brackets must be introduced in the symbolic expression. If parentheses or brackets are not needed, “either” does not affect the translation. A similar point applies to the word “both,” which is often used to introduce conjunctive statements. Here are some disjunctive statements:

 

 

The horseshoe symbol is used to translate “if . . . then . . . ,” “only if,” and similar expressions that indicate a conditional statement. The expressions “in case,” “provided that,” “given that,” and “on condition that” are usually translated in the same way as “if.” By customary usage, the horseshoe symbol is also used to translate “implies.” Although “implies” is used most properly to describe the relationship between the premises and conclusion of an argument, we may accept this translation as an alternate meaning for “implies.”

The function of “only if” is, in a sense, just the reverse of “if.” For example, the statement “You will catch a fish only if your hook is baited” does not mean “If your hook is baited, then you will catch a fish.” If it meant this, then everyone with a baited hook would catch a fish. Rather, the statement means “If your hook is not baited, then you will not catch a fish,” which is logically equivalent to “If you catch a fish, then your hook was baited.” To avoid mistakes in translating “if” and “only if” remember this rule: The statement that follows “if” is always the antecedent, and the statement that follows “only if” is always the consequent. Thus, “C only if H” is translated C ⊃ H, whereas “C if H” is translated H ⊃ C. Additional examples:

In translating conditional statements, it is essential not to confuse antecedent with consequent. The statement A ⊃ B is not logically equivalent to B ⊃ A.

The horseshoe symbol is also used to translate statements phrased in terms of sufficient conditions and necessary conditions. Event A is said to be a sufficient condition for event B whenever the occurrence of A is all that is required for the occurrence of B. On the other hand, event A is said to be a necessary condition for event B whenever B cannot occur without the occurrence of A. For example, having the flu is a sufficient condition for feeling miserable, whereas having air to breathe is a necessary condition for survival. Other things besides having the flu might cause a person to feel miserable, but that by itself is sufficient; other things besides having air to breathe are required for survival, but without air survival is impossible. In other words, air is necessary.

To translate statements involving sufficient and necessary conditions into symbolic form, place the statement that names the sufficient condition in the antecedent of the conditional and the statement that names the necessary condition in the consequent. The mnemonic device “SUN” may be conveniently used to keep this rule in mind. Turning the U sideways creates S ⊃ N, wherein S and N designate sufficient and necessary conditions, respectively. Whatever is given as a sufficient condition goes in the place of the S, and whatever is given as a necessary condition goes in the place of the N:

 

The triple bar symbol is used to translate the expressions “if and only if” and “is a sufficient and necessary condition for”:

Analysis of the first statement reveals that J ≡ O is logically equivalent to (J ⊃ O) • (O ⊃ J). The statement “JFK tightens security only if O’Hare does” is translated J ⊃ O, and “JFK tightens security if O’Hare does” is translated O ⊃ J. Combining the two English statements, we have (J ⊃ O) • (O ⊃ J), which is just a longer way of writing J ≡ O. A similar analysis applies to the second statement. Because the order of the two conjuncts can be reversed, J ≡ O is logically equivalent to O ≡ J. However, when translating such statements, we adopt the convention that the letter representing the first English statement is written to the left of the triple bar, and the letter representing the second English statement is written to the right of the triple bar. Thus, the examples above are translated J ≡ O, and not O ≡ J.

 

Whenever more than two letters appear in a translated statement, we must use parentheses, brackets, or braces to indicate the proper range of the operators. The statement A • B ∨ C, for example, is ambiguous. When parentheses are introduced, this statement becomes either (A • B) ∨ C or A • (B ∨ C). These two statements are not logically equivalent. Thus, with statements such as these, some clue must be found in the English statement that indicates the correct placement of the parentheses in the symbolic statement. Such clues are usually given by commas and semicolons, by such words as “either” and “both,” and by the use of a single predicate in conjunction with two or more subjects.

 

The symbolic expressions that we have used throughout this section to translate meaningful, unambiguous English statements are called well-formed formulas (WFFs). “WFFs” is usually pronounced “woofs.” A well-formed formula is a syntactically correct arrangement of symbols. In English, for example, the expression “there is a cat on the porch” is syntactically correct, but “Porch on the is cat a there” is not syntactically correct. Some examples of symbolic arrangements that are not well-formed formulas are “A ⊃ ∨ B,” “A • B (∨ C),” and “∼∨ B ≡ ⊃ C.”

 

6.2 Truth Functions

The truth value of a compound proposition expressed in terms of one or more logical operators is said to be a function of the truth values of its components. This means that the truth value of the compound proposition is completely determined by the truth values of its components. If the truth values of the components are known, then the truth value of the compound proposition can be calculated from the definitions of the logical operators. Accordingly, a truth function is any compound proposition whose truth value is completely determined by the truth values of its components.

Many compound propositions in ordinary language are not truth functions. For example, the statement “Mary believes that Paul is dishonest” is compound because it contains the statement “Paul is dishonest” as a component. Yet the truth value of the compound statement is not determined by the truth value of the component, because Mary’s beliefs about Paul are not compelled by any attribute that Paul may or may not possess.

 

Definitions of the Logical Operators

The definitions of the logical operators are presented in terms of statement variables, which are lowercase letters (p, q, r, s) that can stand for any statement. For example, the statement variable p could stand for the statements A, A ⊃ B, B ∨ C, and so on.

Statement variables are used to construct statement forms. A statement form is an arrangement of statement variables and operators such that the uniform substitution of statements in place of the variables results in a statement. For example, ∼p and p ⊃ q are statement forms because substituting the statements A and B in place of p and q, respectively, results in the statements ∼A and A ⊃ B. A compound statement is said to have a certain form if it can be produced by substituting statements in place of the letters in that form. Thus, ∼A, ∼(A ∨ B), and ∼[A • (B ∨ C)] are negations because they can be produced by substituting statements in place of p in the form ∼p.

Now let us consider the definition of the tilde operator (negation). This definition is given by a truth table, an arrangement of truth values that shows in every possible case how the truth value of a compound proposition is determined by the truth values of its simple components. The truth table for negation shows how any statement having the form of a negation (∼p) is determined by the truth value of the statement that is negated (p):

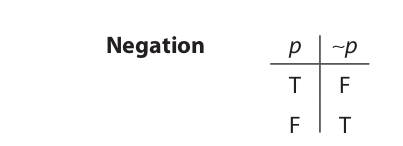
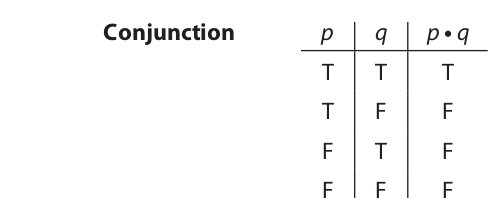
Let us now consider the definition of the dot operator (conjunction). The truth table that follows shows how any statement having the form of a conjunction (p • q) is determined by the truth values of its conjuncts (p, q):

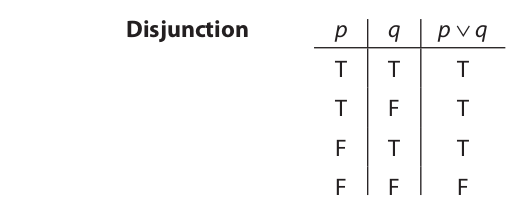
Turning now to the definition of the wedge operator (disjunction), the truth table is as follows:

Let us now consider the horseshoe operator (material implication, or conditional). Its truth table is as follows:

The truth table shows that a conditional statement is false when the antecedent is true and the consequent false and is true in all other cases. This truth-functional interpretation of conditional statements conforms in part with the ordinary meaning of “if . . . then . . .” and in part it diverges. Consider the following examples:

In these statements N, M, and H are true and W and R are false. Thus, according to the truth-functional interpretation, the first statement is true and the second false. This result conforms in large measure to our expectations. But the truth-functional interpretation of the last two statements is true. Although this result may not conflict with our expectations, it is not at all clear why these statements should be considered true.

For an intuitive approach to this problem, imagine that your logic instructor made the following statement: “If you get an A on the final exam, then you will get an A for the course.” Under what conditions would you say that your instructor had lied to you? Clearly, if you got an A on the final exam but did not get an A for the course, you would say that she had lied. This outcome corresponds to a true antecedent and a false consequent. On the other hand, if you got an A on the final exam and also got an A for the course, you would say that she had told the truth (true antecedent, true consequent). But what if you failed to get an A on the final exam? Two alternatives are then possible: Either you got an A for the course anyway (false antecedent, true consequent) or you did not get an A for the course (false antecedent, false consequent). In neither case, though, would you say that your instructor had lied to you. Giving her the benefit of the doubt, you would say that she had told the truth.

 

Lastly, let us consider the definition of the triple bar operator (material equivalence, or biconditional). Its truth table is as follows:

 

Computing the Truth Value of Longer Propositions

The general strategy is to build the truth values of the larger components from the truth values of the smaller ones. In general, the order to be followed in entering truth values is this:

1. Individual letters representing simple propositions
2. Tildes immediately preceding individual letters
3. Operators joining letters or negated letters
4. Tildes immediately preceding parentheses
5. And so on

 

Further Comparison with Ordinary Language

In regard to the dot operator, which is used to translate “and” and “but,” the match is often good; but it fails, at least in part, when the meaning of a conjunctive statement depends on the order of the conjuncts. Consider the following statements:

The first statement implies that the marriage occurred first, and the baby came later, while the second statement implies that the baby came first. This implied meaning is lost in the truth-functional interpretation, because M • B is logically equivalent to B • M.

Another kind of mismatch between the truth functional meaning of conjunctive statements and their ordinary language meaning occurs when the order of the conjuncts implies a causal connection. Example:

The first statement implies that the fall caused the broken arm, but the second statement implies no such thing. However, the truth functional meanings of the two statements are logically equivalent.

For yet another example, consider the following:

The first statement subtly implies that we should buy this car, while the second implies that we should not buy it. But once again, the truth functional interpretations are logically equivalent.

Another instance where the truth-functional interpretation of “and” differs from the ordinary linguistic meaning is offered by slang statements like this one:

The sense of this statement is not that you will in fact go for the gun but rather that, if you go for that gun, then . . . Accordingly, if this statement were interpreted as a truthfunctional conjunction, its meaning would be distorted.

 

In regard to the wedge operator, which is used to translate “or” and “unless,” we saw that the wedge is defined as inclusive disjunction, but we observed that the English word “or” sometimes has the sense of exclusive disjunction. This same observation applies to “unless.” In the following statements, “unless” has an inclusive sense:

The meaning of the first statement includes the case of buying a ticket and not winning, and the meaning of the second includes the case of there being clouds and no rain. In statements like these, where “unless” has an inclusive sense, using the wedge symbol to translate “unless” results in no loss of meaning.

On the other hand, in the following statements “unless” is used in the exclusive sense:

The first statement suggests that the meat cannot be white and at the same time not be properly cooked, and the second suggests that the logs cannot be wet and at the same time be used to make a nice campfire. Thus, if these statements are translated using the wedge operator, part of the meaning will be left out. If this additional part is essential, it can be included by adding the symbolic equivalent of “but not both” to the translation.

 

In connection with the horseshoe operator, we saw that a question arose when the antecedent of a conditional statement turned out to be false. Why, under this circumstance, should the conditional statement be said to be true? For an example of some conditional statements that conform to the truth-functional interpretation, consider the following:

In all three examples the statement remains true even though the antecedent might be false. In the first, even though the temperature does not rise above 32°F at any particular moment, the law that governs the melting point of snow holds true. In other words, the statement (which expresses this law) is true regardless of the truth value of the antecedent. In the second, the mere fact that Figure A might not be a triangle does not affect the fact that a triangle, by definition, has three sides. Thus, the statement (which expresses this fact) is true regardless of the truth value of the antecedent. The third statement expresses a logical relationship between statements. This logical relationship remains unchanged regardless of what the terms A, B, and C are taken to represent. Thus, if A, B, and C represent “dogs,” “cats,” and “birds,” respectively, both antecedent and consequent turn out to be false, but the conditional statement remains true.

As these examples illustrate, the definition of the horseshoe operator matches the meaning of some conditional statements in ordinary language very well. However, in general, the match is far from perfect. The source of the mismatch stems from the fact that the horseshoe operator designates the material conditional, or truth-functional conditional. The material conditional is a kind of conditional statement whose truth value depends purely on the truth or falsity of the antecedent and consequent and not on any inferential connection between antecedent and consequent. Since many conditional statements in ordinary language express such an inferential connection, when the horseshoe operator is used to translate them, part of their meaning is left out. For example, compare the following two statements:

The first statement expresses no inferential connection between antecedent and consequent, so using the horseshoe operator to translate it results in no loss of meaning. However, the second statement does express such a connection. The fact that ice is lighter than water is the reason why it floats. Accordingly, when the horseshoe operator is used to translate the second statement, this special meaning is lost.

The fact that the material conditional ignores inferential connections between antecedent and consequent allows for conflicts between the truth-functional interpretation of a conditional statement and the ordinary interpretation. Consider, for example, the following:

According to their ordinary language interpretation, both of these statements are false. Good senators do not advocate the use of cocaine, and Michigan is far from Miami. Yet, when these statements are interpreted as material conditionals, both turn out to be true, because their antecedents are false. In cases like these, when the truth-functional interpretation of a conditional statement conflicts with the ordinary language interpretation, using the horseshoe operator to translate it may not be appropriate.

 

While inferential relations between antecedent and consequent often play some role in conditionals expressed in the indicative mood (such as those we just considered), they play a dominant role in conditional statements expressed in the subjunctive mood. Consider, for example, the following:

Subjunctive conditionals are often called counterfactual conditionals because their antecedents are typically false. As a result, the only way of determining their truth value in ordinary language is through some kind of inference. Thus, from our knowledge that Bill Gates is rich, we reason that if I were he, then I would be rich. Similarly, from our knowledge that all fish are cold-blooded, we conclude that if dolphins were fish, then they would be cold-blooded. On the other hand, we reason that the second two are false from our knowledge that lead is heavier than air and our knowledge that suicide results in death. Because the truth value of subjunctive conditionals is so closely tied to inferences like these and is so unrelated to the truth or falsity of the components, subjunctive conditionals are generally not considered to be truth functional at all, and the horseshoe operator is not used to translate them. But if they were interpreted truthfunctionally, note that all four of these statements would turn out true, because they have false antecedents.

These observations about conditional statements apply equally to biconditionals. Just as the horseshoe operator expresses material implication, the triple bar operator expresses material equivalence. As such, it ignores any inferential connection between its component statements, and, as a result, conflicts can arise between the ordinary meaning of a biconditional and its truth-functional meaning. Here are two examples of biconditionals expressed in the indicative mood that illustrate such a conflict:

According to the ordinary interpretation, these statements are false. Confessing one’s sins to a priest does not justify anything, and hexagons, by definition, have six sides, not eight. Yet, when these statements are interpreted as expressing material biconditionals, both are true, because in each case the component statements are false. In cases like these, when the ordinary meaning of a biconditional conflicts with the truth-functional meaning, using the triple bar operator to translate it may not be appropriate. Furthermore, as with subjunctive conditionals, subjunctive biconditionals are generally not considered to be truth-functional at all, so the triple bar operator is not used to translate them.

 

6.3 Truth Tables for Propositions

The previous section showed how the truth value of a compound proposition could be determined, given a designated truth value for each simple component. A truth table gives the truth value of a compound proposition for every possible truth value of its simple components. Each line in the truth table represents one such possible arrangement of truth values.

In constructing a truth table the first step is to determine the number of lines (or rows). Because each line represents one possible arrangement of truth values, the total number of lines is equal to the number of possible combinations of truth values for the simple propositions. As we saw in Section 6.2, if there is only one simple proposition, p, the number of lines in the truth table is two, because there are only two possible truth values for p: true, and false. If there are two simple propositions, p and q, there are four lines, because there are four combinations of truth values: p true and q true, p true and q false, p false and q true, and p false and q false. The relationship between the number of different simple propositions and the number of lines in the truth table is expressed as follows:

The relationship between these two columns of numbers is expressed by the formula,

Where L designates the number of lines in the truth table, and n the number of different simple propositions.

 

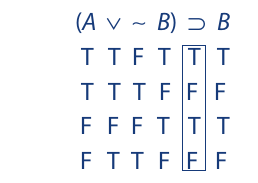
An alternate method for constructing truth tables, which turns out to be faster for certain compound propositions:

 

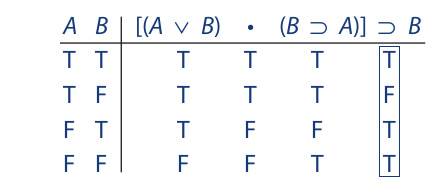
Classifying Statements

Truth tables may be used to determine whether the truth value of a compound statement depends solely on its form or whether it also depends on the specific truth values of its components. A compound statement is said to be a logically true or tautologous statement if it is true regardless of the truth values of its components. It is said to be a logically false or self-contradictory statement if it is false regardless of the truth values of its components. And it is said to be a contingent statement if its truth value varies depending on the truth values of its components. By inspecting the column of truth values under the main operator, we can determine how the compound proposition should be classified:

As the truth table we developed earlier indicates, (C • ∼D) ⊃ E is a contingent proposition. The column under the main operator contains at least one T and at least one F. In other words, the truth value of the compound proposition is “contingent” on the truth values of its components. Sometimes it is true, sometimes false, depending on the truth values of the components.

On the other hand, consider the following truth tables:

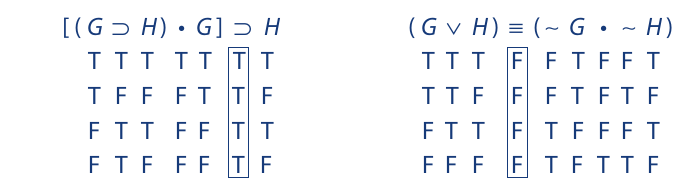
The proposition on the left is tautologous (logically true or a tautology) because the column under the main operator is all true. The one on the right is self-contradictory (logically false) because the main operator column is all false. In neither case is the truth value of the compound proposition contingent on the truth values of the components. The one on the left is true regardless of the truth values of its components—in other words, necessarily true. The one on the right is necessarily false.

If a proposition is either logically true or logically false, its truth value depends merely on its form and has nothing to do with its content. As a result, such statements do not make any genuine assertions about things in the world. For example, the tautologous statement “It is either raining or it is not raining” provides no information about the weather. Similarly, the self-contradictory statement “It is raining and it is not raining” provides no information about the weather. On the other hand, the contingent statement “It is raining in the mountains” does provide information about the weather.

 

Comparing Statements

Truth tables may also be used to determine how two propositions are related to each other. Two propositions are said to be logically equivalent statements if they have the same truth value on each line under their main operators, and they are contradictory statements if they have opposite truth values on each line under their main operators. If neither of these relations hold, the propositions are either consistent or inconsistent. Two (or more) propositions are consistent statements if there is at least one line on which both (or all) of them turn out to be true, and they are inconsistent statements if there is no line on which both (or all) of them turn out to be true. By comparing the main operator columns, one can determine which is the case. However, because the first two relations are stronger than (and may overlap) the second two, the first two relations should be considered first.

For example, the following two propositions are logically equivalent. The main operator columns of their respective truth tables are identical. Note that for proper comparison the columns under K must be identical and the columns under L must be identical.

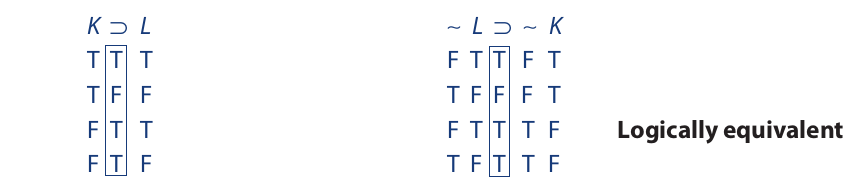
For any two propositions that are logically equivalent, the biconditional statement formed by joining them with a triple bar is tautologous. Thus, (K ⊃ L) ≡ (∼L ⊃ ∼ K) is tautologous. This is easy to see because the columns under the main operators of K ⊃ L and ∼L ⊃ ∼K are identical.

The next two propositions are contradictory:

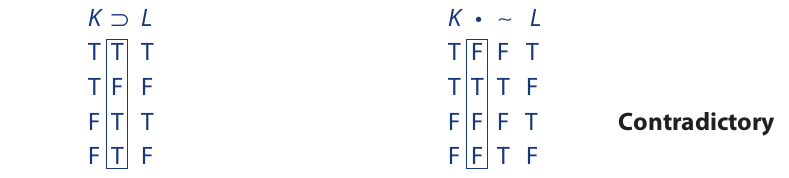
The next two propositions are consistent. On the first line of each truth table the column under the main operator turns out true. This means that it is possible for both propositions to be true, which is the meaning of consistency:

Finally, the next two propositions are inconsistent. There is no line in the columns under the main operators where the truth values are both true:

Any pair of propositions is either consistent or inconsistent. Furthermore, some consistent propositions are also logically equivalent, and some inconsistent propositions are either contradictory or logically equivalent. Because of this partial overlap, pairs of propositions are usually first classified in terms of the stronger of these relations, which are logical equivalence and contradiction. If neither of these stronger relations applies, then the pair of propositions is classified in terms of the weaker relations, consistency and inconsistency.

Unlike logical equivalence and contradiction, which usually relate exactly two propositions, consistency and inconsistency often apply to larger groups of propositions. For consistency, the only requirement is that there be at least one line in the group of truth tables where all of the propositions are true, and for inconsistency the only requirement is that there be no such line. As a result of these requirements, the statement consisting of the conjunction of a group of inconsistent propositions will always be self-contradictory, whereas the statement consisting of the conjunction of a group of consistent propositions will never be self-contradictory.

Consistency and inconsistency are important because, among other things, they can be used to evaluate the overall rationality of a person’s stated position on something. If the statements expressing such a position are consistent, then there is at least a possibility that the position makes sense. This is so because there will be at least one line in the group of truth tables where all of the person’s statements are true. On the other hand, if the statements are inconsistent, then there is no possibility that the position makes sense. In this case there is no line in the truth tables where all of the statements are true. The group of statements, conjoined together, amounts to a self-contradiction.

The truth tables for consistency and logical equivalence also illustrate the important difference between two propositions being factually true and their being logically equivalent. For example, the statements “Water boils at 100°C” and “The current population of the United States is over 200 million” are both true in the present actual world. This real-world situation conforms to the one truth-table line on which both statements are true. As a result of this line, the two statements are consistent. However, they are not logically equivalent, because their truth values are not necessarily the same. The truth value of the second proposition might change in the future, while that of the first would remain the same. An analogous distinction, incidentally, holds between two statements having actually opposite truth values and their being contradictory.

 

6.4 Truth Tables for Arguments

Truth tables provide the standard technique for testing the validity of arguments in propositional logic. To construct a truth table for an argument, follow these steps:

1. Symbolize the arguments using letters to represent the simple propositions.
2. Write out the symbolized argument, placing a single slash between the premises and a double slash between the last premise and the conclusion.
3. Draw a truth table for the symbolized argument as if it were a proposition broken into parts, outlining the columns representing the premises and conclusion.
4. Look for a line in which all of the premises are true and the conclusion is false. If such a line exists, the argument is invalid; if not, it is valid.

For example, let us test the following argument for validity:

The first step is to symbolize the argument:

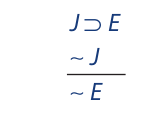
Now a truth table may be constructed. Since the symbolized argument contains two different letters, the truth table has four lines. Make sure that identical letters have identical columns beneath them. Here are the columns for the individual letters:

The truth table is now completed, and the columns representing the premises and conclusion are outlined:

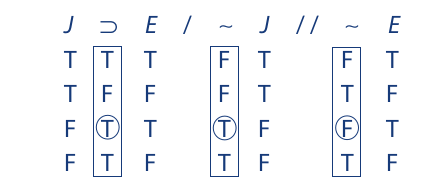
Inspection of the third line reveals that both of the premises are true and the conclusion is false. The argument is therefore invalid.

Another example:

The completed truth table is this:

Inspection of the truth table reveals that there is no line on which both premises are true and the conclusion is false. The argument is therefore valid.

The logic behind the method of truth tables is easy to understand. By definition, a valid argument is one in which it is not possible for the premises to be true and the conclusion false. A truth table presents every possible combination of truth values that the components of an argument may have. Therefore, if no line exists on which the premises are true and the conclusion false, then it is not possible for the premises to be true and the conclusion false, in which case the argument is valid. Conversely, if there is a line on which the premises are true and the conclusion false, then it is possible for the premises to be true and the conclusion false, and the argument is invalid. Accordingly, to test the validity of an argument, use this procedure:

Truth tables provide a convenient illustration of the fact that any argument having inconsistent premises is valid regardless of what its conclusion may be, and any argument having a tautologous conclusion is valid regardless of what its premises may be. Example:

Since the premises of this argument are inconsistent, there is no line on which the premises are both true. Accordingly, there is no line on which the premises are both true and the conclusion false, so the argument is valid. Of course, the argument is unsound, because it has a false premise. Another example:

The conclusion of this argument is a tautology. Accordingly, there is no line on which the premise is true and the conclusion false, and so the argument is valid. Incidentally, it is also sound, because the premise is true.

The conditional statement having the conjunction of an argument’s premises as its antecedent and the conclusion as its consequent is called the argument’s corresponding conditional. For example, the corresponding conditional of the second argument tested in this section is [(O ⊃ ∼T) • (∼T ⊃ B)] ⊃ (O ⊃ B). For any valid argument (such as this one), the corresponding conditional is a tautology. This is easy to see. In any valid argument, there is no line on which the premises are all true and the conclusion false. Thus, in the corresponding conditional, there is no line on which the antecedent is true and the consequent false, so the corresponding conditional is true on every line.

 

6.5 Indirect Truth Tables

Indirect truth tables provide a shorter and faster method for testing the validity of arguments than do ordinary truth tables. This method is especially applicable to arguments that contain a large number of different simple propositions. For example, an argument containing five different simple propositions would require an ordinary truth table having thirty-two lines. The indirect truth table for such an argument, on the other hand, would usually require only a single line and could be constructed in a fraction of the time required for the ordinary truth table. Indirect truth tables can also be used to test a series of statements for consistency.

 

Preliminary Skills

Using indirect truth tables requires developing the skill to work backwards from the truth value of the main operator of a compound statement to the truth values of its simple components. Suppose, for example, that you are given a conjunctive statement that is true:

Because a conjunctive statement can be true in only one way, you know immediately that both A and B are true:

Suppose, on the other hand, that you are given a conditional statement that is false:

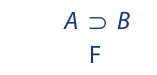
Since a conditional statement can be false in only one way, you know that A is true and B is false:

 

Testing Arguments for Validity

To construct an indirect truth table for an argument, we begin by assuming that the argument is invalid. That is, we assume that it is possible for the premises to be true and the conclusion false. Truth values corresponding to true premises and false conclusion are entered beneath the main operators for the premises and conclusion. Then, working backward, the truth values of the separate components are derived. If no contradiction is obtained in the process, this means that it is indeed possible for the premises to be true and the conclusion false, as originally assumed, so the argument is therefore invalid. If, however, the attempt to make the premises true and the conclusion false necessarily leads to a contradiction, it is not possible for the premises to be true and the conclusion false, in which case the argument is valid. Consider the following symbolized argument:

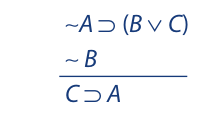
We begin as before by writing the symbolized argument on a single line, placing a single slash between the premises and a double slash between the last premise and the conclusion. Then we assign T to the premises and F to the conclusion:

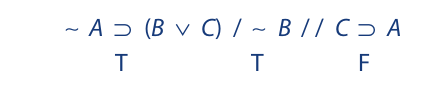
We can now derive the truth values of B, C, and A, as follows:

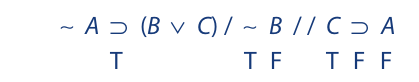
These truth values are now transferred to the first premise:

We thus have a perfectly consistent assignment of truth values, which makes the premises true and the conclusion false. The argument is therefore invalid. If an ordinary truth table were constructed for this argument, it would be seen that the argument fails on the line on which A is false, B is false, and C is true. This is the exact arrangement presented in the indirect truth table just presented.

Here is another example. As always, we begin by assigning T to the premises and F to the conclusion:

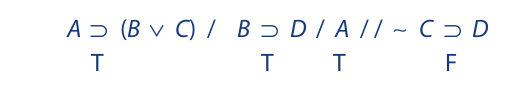
From the conclusion we can now derive the truth values of C and D, which are then transferred to the first two premises:

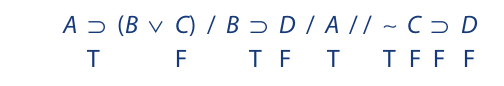
The truth value of B is now derived from the second premise and transferred, together with the truth value of A, to the first premise:

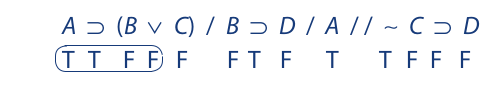
A contradiction now appears in the truth values assigned to the first premise, since T ⊃ F is F. The inconsistent truth values are circled. Because every step was strictly necessitated by some prior step, we have shown that it is impossible for the premises to be true and the conclusion false. The argument is therefore valid.

Sometimes a single row of truth values is not sufficient to prove an argument valid. Example:

Since a conditional statement can be true in any one of three ways, and a conjunctive statement can be false in any one of three ways, merely assigning truth to the premises and falsity to the conclusion of this argument is not sufficient to obtain the truth values of any of the component statements. When faced with a situation such as this, we must list all of the possible ways that one of the premises can be true or the conclusion false, and proceed from there. If we list all of the possible ways the conclusion may be false, we obtain the following:

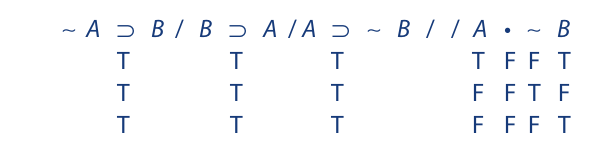
Extending the truth values of A and B to the premises, we obtain the following result:

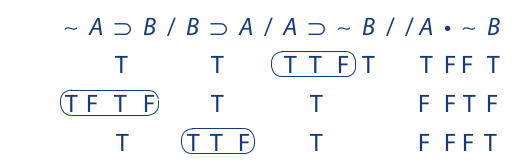
Since each line necessarily leads to a contradiction, the argument is valid. If a contradiction had been avoided on some line, the argument would, of course, be invalid, because it would be possible for the premises to be true and the conclusion false. Note that in this argument it is not necessary to fill out all the truth values on any one line to be forced into a contradiction. On each line the contradiction is necessarily derived within the context of a single premise.

If an indirect truth table requires more than one line, the method to be followed is this. Either select one of the premises and compute all of the ways it can be made true, or select the conclusion and compute all of the ways it can be made false. This selection should be dictated by the requirement of simplicity. For example, if the conclusion can be made false in only two ways, while each of the premises can be made true in three ways, then select the conclusion. On the other hand, if one of the premises can be made true in only two ways while the conclusion can be made false in three ways, then select that premise. If neither of these situations prevails, then select the conclusion.

Having made your selection, proceed to compute the truth values of each line, beginning with the first. If no contradiction is derived on this line, stop! The argument has been proved invalid. If a contradiction is derived on the first line, proceed to the second line. If no contradiction is derived on this line, then, again, the argument has been proved invalid. If a contradiction is derived, proceed to the third line, and so on. Remember, the objective is to produce a line having no contradiction. Once such a line is produced, the argument has been proved invalid, and no further work need be done. If, on the other hand, each line necessarily leads to a contradiction, the argument is valid.

Three final points need to be made about indirect truth tables for arguments. First, if a contradiction is obtained in the assignment of truth values, every step leading to it must be logically implied by some prior step. In other words, the contradiction must be unavoidable. If a contradiction is obtained after truth values are assigned haphazardly or by guessing, then nothing has been proved. The objective is not to produce a contradiction but to avoid one (if possible).

For example, in the following indirect truth table a contradiction is apparent in the first premise:

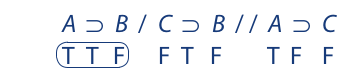
Yet the argument is invalid. The contradiction that appears is not required by the assignment of truth to the premises and falsity to the conclusion. The following indirect truth table, which is done correctly, proves the argument invalid:

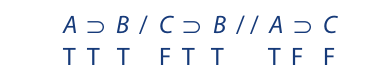
The second point is that for valid arguments the order in which the truth values are assigned may affect where the contradiction is obtained. That is, depending on the order of assignment, the contradiction may appear in the first premise, second premise, third premise, and so on. But, of course, the order of assignment does not affect the final determination of validity.

The last point is that it is essential that identical letters be assigned identical truth values. For example, if the letter A appears three times in a certain symbolized argument and the truth value T is assigned to it in one occurrence, then the same truth value must be assigned to it in the other occurrences as well. After the truth table has been completed, each letter should be rechecked to ensure that one and the same truth value has been assigned to its various occurrences.

 

Testing Statements for Consistency

The method for testing a series of statements for consistency is similar to the method for testing arguments. We begin by writing the statements on a line, separating each with a single slash mark. (Since we have no conclusion, we use no double slash marks.) Then we assume that the statements are consistent. We assign a T to the main operator of each, and we then compute the truth values of the components. If this computation leads necessarily to a contradiction, the statements are not as we assumed them to be. That is, they are inconsistent. But if no contradiction is reached, the statements are consistent. Here is an example:

First, we write the statements on a single line separated by a single slash mark; we then assign T to each of the main operators:

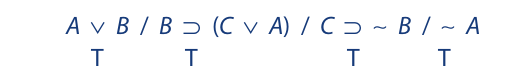
Next, we compute the truth values of the components. First we compute the truth value of A. Next, we enter this truth value in the first statement and compute the truth value of B. Next, we enter the truth value of B in the second statement and compute the truth value of C. Finally, the truth values of C and B are carried to the third statement:

Since this computation leads necessarily to a contradiction (third statement), the group of statements is inconsistent.

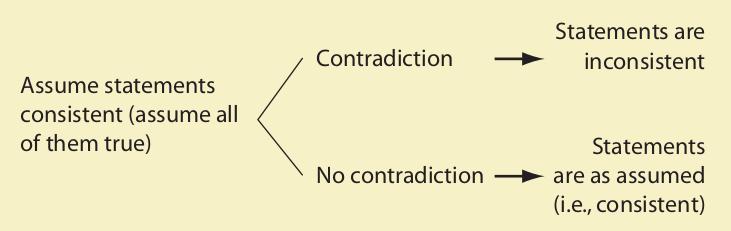
Here is another example. The statements are written on a single line, and a T is assigned to each of the main operators:

Since all of the statements can be true in three ways, we select one of them (the fourth) and figure all of the ways it can be true:

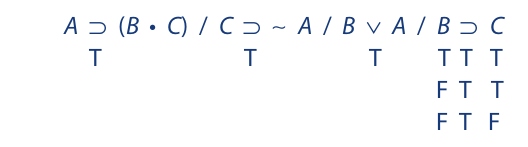
Filling out the first line leads to no contradiction, so the statements are consistent:

As with testing arguments, the objective is to avoid a contradiction. As soon as no contradiction is reached, we stop. The statements are consistent. Only if all three lines had led to a contradiction would these statements be inconsistent.

 

6.6 Argument Forms and Fallacies

Many of the arguments that occur in propositional logic have forms that bear specific names and can be immediately recognized as either valid or invalid. The first part of this section presents some of the more common ones and explains how they are recognized. The second part discusses ways of refuting two of these forms, constructive and destructive dilemmas. The third part presents a word of caution relating to invalid forms. Finally, the fourth part applies to real-life arguments some of the principles developed in the first part.

 

Common Argument Forms

An argument form is an arrangement of statement variables and operators such that the uniform replacement of the variables by statements results in an argument. A valid argument form is any argument form that satisfies the truth-table test.

The first valid argument form to consider is disjunctive syllogism, which is defined as follows:

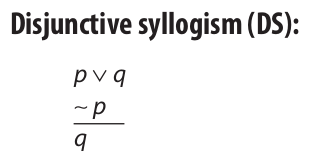
The validity of this form can be easily checked by a truth table. Now, given that validity is purely a function of the form of an argument, any argument produced by uniformly substituting statements in place of the variables in this argument form is a valid argument. Such an argument is said to have the form of a disjunctive syllogism. The following argument was produced in this way and is therefore valid:

The validity of a disjunctive syllogism arises from the fact that one of the premises presents two alternatives and the other premise eliminates one of those alternatives, leaving the other as the conclusion. This so-called “method of elimination” is essential to the validity of a disjunctive syllogism. If one premise should present two alternatives and the other premise should affirm one of those alternatives, the argument is invalid (unless the conclusion is a tautology). Example:

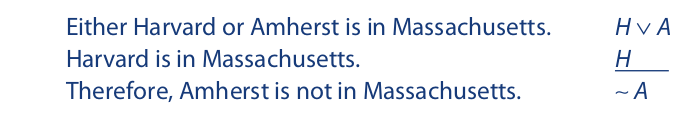
Since both Harvard and Amherst are in Massachusetts, the premises are true and the conclusion is false. Thus, the argument is invalid. Because the wedge symbol designates inclusive disjunction, the disjunctive premise includes the possibility of both disjuncts being true. Thus, for the argument to be valid, the other premise must eliminate one of the disjuncts.

 

The next valid argument form we consider is pure hypothetical syllogism. It consists of two premises and one conclusion, all of which are hypothetical (conditional) statements, and is defined as follows:

Any argument that has the form of a pure hypothetical syllogism (that is, any argument that can be produced by uniformly substituting statements in place of the variables in the form) is a valid argument. Example:

The validity of a pure hypothetical syllogism is grounded in the fact that the premises link together like a chain. In the population argument, the consequent of the first premise is identical to the antecedent of the second. If the premises fail to link together in this way, the argument may be invalid. Example:

The premises of this argument are true, and the conclusion is false. Thus, the argument is invalid.

 

Another important valid argument form is called modus ponens (“asserting mode”). It consists of a conditional premise, a second premise that asserts the antecedent of the conditional premise, and a conclusion that asserts the consequent:

Any argument having the form of modus ponens is a valid argument. Example:

 

Closely associated with modus ponens is modus tollens (“denying mode”). Modus tollens is a valid argument form consisting of one conditional premise, a second premise that denies the consequent of the conditional premise, and a conclusion that denies the antecedent. It is defined as follows:

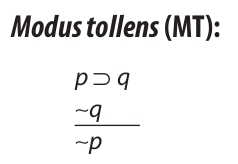
Although a little harder to understand than modus ponens, modus tollens can be understood by the following reasoning process: The conclusion states that we do not have p, because if we did have p, then (by the first premise) we would have q, and we do not have q (by the second premise). Any argument that has the form of modus tollens is a valid argument. Example:

 

A constructive dilemma is a valid argument form that consists of a conjunctive premise made up of two conditional statements, a disjunctive premise that asserts the antecedents in the conjunctive premise (like modus ponens), and a disjunctive conclusion that asserts the consequents of the conjunctive premise. It is defined as follows:

Any argument that has the form of a constructive dilemma is a valid argument. Example:

 

The destructive dilemma is also a valid argument form. It is similar to the constructive dilemma in that it includes a conjunctive premise made up of two conditional statements and a disjunctive premise. However, the disjunctive premise denies the consequents of the conditionals (like modus tollens), and the conclusion denies the antecedents:

Any argument that has the form of a destructive dilemma is a valid argument. Example:

 

Two invalid forms are closely associated with modus ponens and modus tollens. These are affirming the consequent and denying the antecedent. Affirming the consequent consists of one conditional premise, a second premise that asserts the consequent of the conditional, and a conclusion that asserts the antecedent:

Any argument that has the form of affirming the consequent is an invalid argument.* The following argument has this form and is therefore invalid:

Given that this argument has true premises and a false conclusion, it is clearly invalid.

 

Denying the antecedent consists of a conditional premise, a second premise that denies the antecedent of the conditional, and a conclusion that denies the consequent:

Any argument that has the form of denying the antecedent is an invalid argument. Example:

Again, this argument has true premises and a false conclusion, so it is clearly invalid.

 

Refuting Constructive and Destructive Dilemmas

Now that we are familiar with several argument forms in propositional logic, we may return for a closer look at two of them, constructive and destructive dilemmas. Arguments having these forms occur frequently in public debate, where an arguer may use them to trap an opponent. Since both forms are valid, the only direct mode of defense available to the opponent is to prove the dilemma unsound. This can be done by proving at least one of the premises false. If the conjunctive premise (otherwise called the “horns of the dilemma”) is proven false, the opponent is said to have “grasped the dilemma by the horns.” This, of course, may be done by proving either one of the conditional statements false. If, on the other hand, the disjunctive premise is proven false, the opponent is said to have “escaped between the horns of the dilemma.” The latter strategy often involves finding a third alternative that excludes the two that are given in the disjunctive premise. If such a third alternative can be found, both of the given disjuncts will be proved false. Consider the following constructive dilemma:

It is easy to escape between the horns of this dilemma by arguing that taxes could be kept as they are, in which case they would neither increase nor decrease.

Some dilemmas, however, do not allow for the possibility of escaping between the horns. Consider the following constructive dilemma:

Since the disjunctive premise of this dilemma is a tautology, it cannot be proven false. This leaves the strategy of grasping the dilemma by the horns, which may be done by proving either of the conditional statements in the conjunctive premise false. One debater might want to attack the first conditional and argue that competition and peace can coexist, while another might want to attack the second and argue that progress can be achieved through some means other than encouraging competition.

The strategy to be followed in refuting a dilemma is therefore this: Examine the disjunctive premise. If this premise is a tautology, attempt to grasp the dilemma by the horns by attacking one or the other of the conditional statements in the conjunctive premise. If the disjunctive premise is not a tautology, then either escape between the horns by, perhaps, finding a third alternative, or grasp the dilemma by the horns— whichever is easier.

A third, indirect strategy for refuting a dilemma involves constructing a counterdilemma. This is typically done by changing either the antecedents or the consequents of the conjunctive premise while leaving the disjunctive premise as it is, so as to obtain a different conclusion. If the dilemma in question is a constructive dilemma, the consequents of the conjunctive premise are changed. Here are possible counterdilemmas for the two dilemmas just presented:

Constructing a counterdilemma falls short of a refutation of a given dilemma because it merely shows that a different approach can be taken to a certain problem. It does not cast any doubt on the soundness of the original dilemma. Yet the strategy is often effective because it testifies to the cleverness of the debater who can accomplish it successfully. In the heat of debate the attending audience is often persuaded that the original argument has been thoroughly demolished.

 

Note on Invalid Forms

Throughout this book we have seen that any substitution instance of a valid argument form is a valid argument. For example, consider modus ponens:

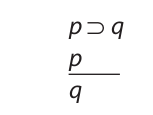
Literally any two statements uniformly substituted in the place of p and q will result in a valid argument. Thus, the following symbolized arguments both have the form of modus ponens, and are accordingly valid:

In the first argument S and T are uniformly substituted in the place of p and q, and in the second argument K ∨ B and N • R are uniformly substituted in the place of p and q.

However, this result does not extend to invalid argument forms. Consider, for example, affirming the consequent:

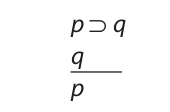
Sometimes the uniform substitution of statements in the place of p and q results in an invalid argument, and sometimes it does not. Both of the following symbolized arguments are substitution instances of affirming the consequent, but the one on the left is invalid while the one on the right is valid:

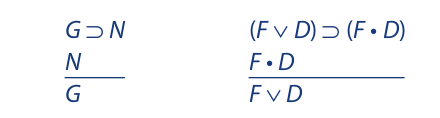
To deal with this problem we adopt a convention about when an argument will be said to have an invalid form. We will say that an argument has an invalid form if it is a substitution instance of that form and it is not a substitution instance of any valid form. According to this convention only the argument on the left has the form of affirming the consequent. The argument on the right does not have this form because it is a substitution instance of the following valid form:

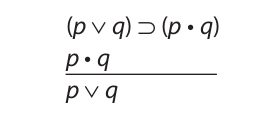
The validity of this form results from the fact that the conclusion follows from the second premise alone, without any involvement of the first premise. This fact may be easily checked with a truth table.

Here is another invalid form:

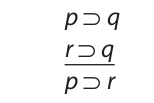
Both of the following symbolized arguments are substitution instances of this form, but only the one on the left is invalid:

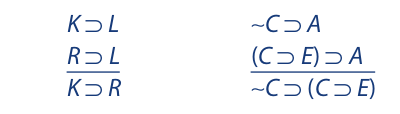
The argument on the right is valid because its conclusion is a tautology. Accordingly, only the argument on the left will be said to have the invalid form in question.

The point of this discussion is that when we attempt to determine the validity of arguments through mere inspection, we have to exert caution with invalid forms. The mere fact that an argument is a substitution instance of an invalid form does not guarantee that it is invalid. Before judging it invalid we must make sure that it is not valid for some other reason, such as its conclusion being a tautology. However, as concerns the exercises at the end of this section, all of the arguments that are substitution instances of invalid forms are invalid. In other words, none of them is like either of the right-hand examples considered in these paragraphs.

 

Summary and Application

Any argument having one of the following forms is valid:

Any argument having either of the following forms is invalid:

In identifying arguments as having these argument forms, use the following procedure. First symbolize the argument, using uppercase letters for the simple propositions. Then see whether the symbolized argument fits the pattern of one of these forms.