LeetCode - Minimum Path Sum

Given a m x n grid filled with non-negative numbers, find a path from top left to bottom right, which minimizes the sum of all numbers along its path.

Note: You can only move either down or right at any point in time.

 

Example 1:

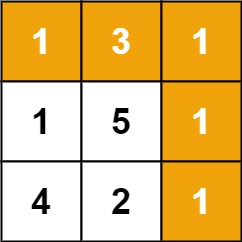
Input: grid = [[1,3,1],[1,5,1],[4,2,1]]
Output: 7
Explanation: Because the path 1 → 3 → 1 → 1 → 1 minimizes the sum.

Example 2:

Input: grid = [[1,2,3],[4,5,6]]
Output: 12

 

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 200
• 0 <= grid[i][j] <= 200

 

My Solution:

class Solution:
    def minPathSum(self, grid: List[List[int]]) -> int:
        m, n = len(grid), len(grid[0])
        
        dp = [[float('inf')] * n for _ in range(m)]
        dp[0][0] = grid[0][0]

        for j in range(1, n):
            dp[0][j] = dp[0][j - 1] + grid[0][j]
        for i in range(1, m):
            dp[i][0] = dp[i - 1][0] + grid[i][0]
        
        for i in range(1, m):
            for j in range(1, n):
                dp[i][j] = min(dp[i][j - 1], dp[i - 1][j]) + grid[i][j]
        
        return dp[m - 1][n - 1]