LeetCode - Binary Tree Maximum Path Sum

A path in a binary tree is a sequence of nodes where each pair of adjacent nodes in the sequence has an edge connecting them. A node can only appear in the sequence at most once. Note that the path does not need to pass through the root.

The path sum of a path is the sum of the node's values in the path.

Given the root of a binary tree, return the maximum path sum of any non-empty path.

 

Example 1:

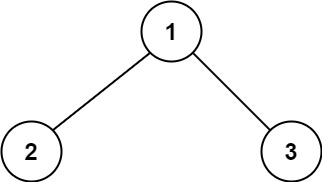
Input: root = [1,2,3]
Output: 6
Explanation: The optimal path is 2 -> 1 -> 3 with a path sum of 2 + 1 + 3 = 6.

Example 2:

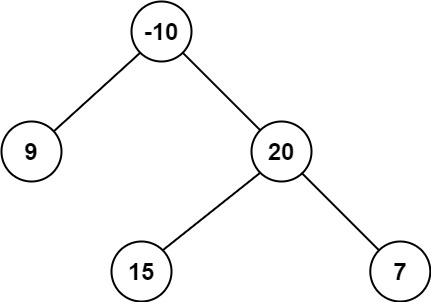
Input: root = [-10,9,20,null,null,15,7]
Output: 42
Explanation: The optimal path is 15 -> 20 -> 7 with a path sum of 15 + 20 + 7 = 42.

 

Constraints:

• The number of nodes in the tree is in the range [1, 3 * 104].
• -1000 <= Node.val <= 1000

 

ChatGPT's Solution:

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def maxPathSum(self, root: Optional[TreeNode]) -> int:
        # Initialize the result as the smallest possible integer
        self.max_sum = float('-inf')

        # Helper function that computes the maximum path sum through the current node
        def dfs(node):
            if not node:
                return 0  # Return 0 for a null node, as it does not contribute to the sum
            
            # Recursively calculate the max path sum for left and right subtrees
            left_gain = max(dfs(node.left), 0)  # If negative, we discard it (take 0 instead)
            right_gain = max(dfs(node.right), 0)  # If negative, we discard it (take 0 instead)

            # Calculate the price to start a new path at this node
            price_newpath = node.val + left_gain + right_gain

            # Update the global max_sum if the new path is better
            self.max_sum = max(self.max_sum, price_newpath)

            # Return the maximum sum path starting from the current node and extending to either left or right
            return node.val + max(left_gain, right_gain)
        
        # Start DFS traversal
        dfs(root)

        # Return the global max path sum
        return self.max_sum