Patterns
Graph pattern matching sits at the very core of Cypher®. It is the mechanism used to navigate, describe and extract data from a graph by applying a declarative pattern. Inside a MATCH clause, you can use graph patterns to define the data you are searching for and the data to return. Graph pattern matching can also be used without a MATCH clause, in the subqueries EXISTS, COUNT, and COLLECT.
A graph pattern describes data using a syntax that is similar to how the nodes and relationships of a property graph are drawn on a whiteboard. On a whiteboard, nodes are drawn as circles and relationships are drawn as arrows. Cypher represents the circles as a pair of parentheses, and the arrows as dashes and greater-than or less-than symbols:
()-->()<--()These simple patterns for nodes and relationships form the building blocks of path patterns that can match paths of a fixed length. As well as discussing simple fixed-length patterns, this chapter covers more complex patterns, showing how to match patterns of a variable or unknown length, find the shortest paths between a given set of nodes, add inline filters for improved query performance, and add cycles and non-linear shapes to path patterns.
Fixed-length patterns
The most basic form of graph pattern matching in Cypher® involves the matching of fixed-length patterns. This includes node patterns, relationship patterns, and path patterns.
Node patterns
Every graph pattern contains at least one node pattern. The simplest graph pattern is a single, empty node pattern:
MATCH ()The empty node pattern matches every node in a property graph. In order to obtain a reference to the nodes matched, a variable needs to be declared in the node pattern:
MATCH (n)With this reference, node properties can be accessed:
MATCH (n)
RETURN n.nameAdding a label expression to the node pattern means only nodes with labels that match will be returned. The following matches nodes that have the Stop label:
MATCH (n:Stop)The following more complex label expression matches all nodes that are either a TrainStation and a BusStation or StationGroup:
MATCH (n:(TrainStation&BusStation)|StationGroup)A map of property names and values can be used to match on node properties based on equality with the specified values. The following matches nodes that have their mode property equal to Rail:
MATCH (n { mode: 'Rail' })More general predicates can be expressed with a WHERE clause. The following matches nodes whose name property starts with Preston:
MATCH (n:Station WHERE n.name STARTS WITH 'Preston')
RETURN nRelationship patterns
The simplest possible relationship pattern is a pair of dashes:
--This pattern matches a relationship with any direction and does not filter on any relationship type or property. Unlike a node pattern, a relationship pattern cannot be used in a MATCH clause without node patterns at both ends. See path patterns for more details.
In order to obtain a reference to the relationships matched by the pattern, a relationship variable needs to be declared in the pattern by adding the variable name in square brackets in between the dashes:
-[r]-To match a specific direction, add < or > to the left or right hand side respectively:
-[r]->To match on a relationship type, add the type name after a colon:
-[:CALLS_AT]->Similar to node patterns, a map of property names and values can be added to filter on properties of the relationship based on equality with the specified values:
-[{ distance: 0.24, duration: 'PT4M' }]->A WHERE clause can be used for more general predicates:
-[r WHERE time() + duration(r.duration) < time('22:00') ]->Path patterns
Any valid path starts and ends with a node, with relationships between each node (if there is more than one node). Fixed-length path patterns have the same restrictions, and for all valid path patterns the following are true:
-
They have at least one node pattern.
-
They begin and end with a node pattern.
-
They alternate between nodes and relationships.
These are all valid path patterns:
()(s)--(e)(:Station)--()<--(m WHERE m.departs > time('12:00'))-->()-[:NEXT]->(n)These are invalid path patterns:
-->()-->()-->-->()
Variable-length patterns
Cypher® can be used to match patterns of a variable or an unknown length. Such patterns can be found using quantified path patterns and quantified relationships. This page also discusses how variables work when declared in quantified path patterns (group variables), and how to use predicates in quantified path patterns.
Quantified path patterns
This section considers how to match paths of varying length by using quantified path patterns, allowing you to search for paths whose lengths are unknown or within a specific range.
Quantified path patterns can be useful when, for example, searching for all nodes that can be reached from an anchor node, finding all paths connecting two nodes, or when traversing a hierarchy that may have differing depths.
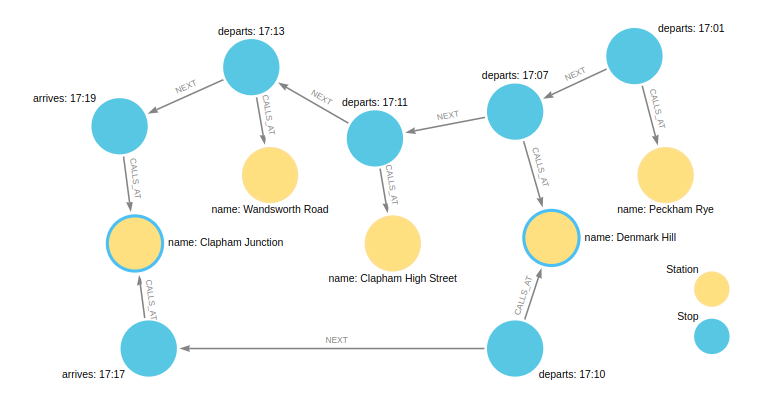
CREATE (pmr:Station {name: 'Peckham Rye'}),
(dmk:Station {name: 'Denmark Hill'}),
(clp:Station {name: 'Clapham High Street'}),
(wwr:Station {name: 'Wandsworth Road'}),
(clj:Station {name: 'Clapham Junction'}),
(s1:Stop {arrives: time('17:19'), departs: time('17:20')}),
(s2:Stop {arrives: time('17:12'), departs: time('17:13')}),
(s3:Stop {arrives: time('17:10'), departs: time('17:11')}),
(s4:Stop {arrives: time('17:06'), departs: time('17:07')}),
(s5:Stop {arrives: time('16:58'), departs: time('17:01')}),
(s6:Stop {arrives: time('17:17'), departs: time('17:20')}),
(s7:Stop {arrives: time('17:08'), departs: time('17:10')}),
(clj)<-[:CALLS_AT]-(s1), (wwr)<-[:CALLS_AT]-(s2),
(clp)<-[:CALLS_AT]-(s3), (dmk)<-[:CALLS_AT]-(s4),
(pmr)<-[:CALLS_AT]-(s5), (clj)<-[:CALLS_AT]-(s6),
(dmk)<-[:CALLS_AT]-(s7),
(s5)-[:NEXT {distance: 1.2}]->(s4),(s4)-[:NEXT {distance: 0.34}]->(s3),
(s3)-[:NEXT {distance: 0.76}]->(s2), (s2)-[:NEXT {distance: 0.3}]->(s1),
(s7)-[:NEXT {distance: 1.4}]->(s6)
Quantified path patterns
Quantified path patterns solve this problem by extracting repeating parts of a path pattern into parentheses and applying a quantifier. That quantifier specifies a range of possible repetitions of the extracted pattern to match on. For the current example, the first step is identifying the repeating pattern, which in this case is the sequence of alternating Stop nodes and NEXT relationships, representing one segment of a Service:
(:Stop)-[:NEXT]->(:Stop)The shortest path has one instance of this pattern, the longest three. So the quantifier applied to the wrapper parentheses is the range one to three, expressed as {1,3}:
((:Stop)-[:NEXT]->(:Stop)){1,3}This also includes repetitions of two.
MATCH (:Station { name: 'Denmark Hill' })<-[:CALLS_AT]-(d:Stop)
((:Stop)-[:NEXT]->(:Stop)){1,3}
(a:Stop)-[:CALLS_AT]->(:Station { name: 'Clapham Junction' })
RETURN d.departs AS departureTime, a.arrives AS arrivalTime
Quantified relationships
Quantified relationships allow some simple quantified path patterns to be re-written in a more succinct way. Consider the following query:
MATCH (d:Station { name: 'Denmark Hill' })<-[:CALLS_AT]-(n:Stop)
((:Stop)-[:NEXT]->(:Stop)){1,10}
(m:Stop)-[:CALLS_AT]->(a:Station { name: 'Clapham Junction' })
WHERE m.arrives < time('17:18')
RETURN n.departs AS departureTime
If the relationship NEXT only connects Stop nodes, the :Stop label expressions can be removed:
MATCH (d:Station { name: 'Denmark Hill' })<-[:CALLS_AT]-(n:Stop)
(()-[:NEXT]->()){1,10}
(m:Stop)-[:CALLS_AT]->(a:Station { name: 'Clapham Junction' })
WHERE m.arrives < time('17:18')
RETURN n.departs AS departureTime
When the quantified path pattern has one relationship pattern, it can be abbreviated to a quantified relationship. A quantified relationship is a relationship pattern with a postfix quantifier. Below is the previous query rewritten with a quantified relationship:
MATCH (d:Station { name: 'Denmark Hill' })<-[:CALLS_AT]-
(n:Stop)-[:NEXT]->{1,10}(m:Stop)-[:CALLS_AT]->
(a:Station { name: 'Clapham Junction' })
WHERE m.arrives < time('17:18')
RETURN n.departs AS departureTime
The scope of the quantifier {1,10} is the relationship pattern -[:NEXT]-> and not the node patterns abutting it. More generally, where a path pattern contained in a quantified path pattern has the following form:
(() <relationship pattern> ()) <quantifier>then it can be re-written as follows:
<relationship pattern> <quantifier>Group variables
This section uses the example of Stations and Stops used in the previous section, but with an additional property distance added to the NEXT relationships:
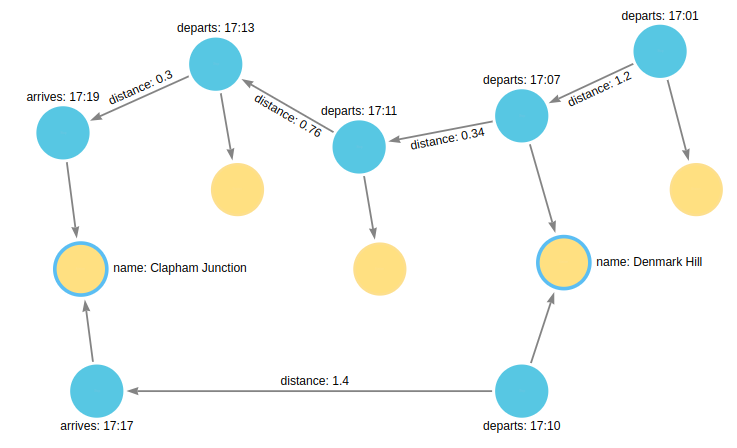
As the name suggests, this property represents the distance between two Stops. To return the total distance for each service connecting a pair of Stations, a variable referencing each of the relationships traversed is needed. Similarly, to extract the departs and arrives properties of each Stop, variables referencing each of the nodes traversed is required. In this example of matching services between Denmark Hill and Clapham Junction, the variables l and m are declared to match the Stops and r is declared to match the relationships. The variable origin only matches the first Stop in the path:
MATCH (:Station { name: 'Denmark Hill' })<-[:CALLS_AT]-(origin)
((l)-[r:NEXT]->(m)){1,3}
()-[:CALLS_AT]->(:Station { name: 'Clapham Junction' })
Variables that are declared inside quantified path patterns are known as group variables. They are so called because, when referred outside of the quantified path pattern, they are lists of the nodes or relationships they are bound to in the match.
Returning to the original goal, which was to return the sequence of depart times for the Stops and the total distance of each service, the final query exploits the compatibility of group variables with list comprehensions and list functions such as reduce():
MATCH (:Station {name: 'Denmark Hill'})<-[:CALLS_AT]-(origin)
((l)-[r:NEXT]->(m)){1,3}
()-[:CALLS_AT]->(:Station {name: 'Clapham Junction'})
RETURN origin.departs + [stop in m | stop.departs] AS departureTimes,
reduce(acc = 0.0, next in r | round(acc + next.distance, 2)) AS totalDistance
Predicates in quantified path patterns
One of the pitfalls of quantified path patterns is that, depending on the graph, they can end up matching very large numbers of paths, resulting in a slow query performance. This is especially true when searching for paths with a large maximum length or when the pattern is too general. However, by using inline predicates that specify precisely which nodes and relationships should be included in the results, unwanted results will be pruned as the graph is traversed.
Here are some examples of the types of constraints you can impose on quantified path pattern traversals:
-
Nodes must have certain combinations of labels. For example, all nodes must be an
Employee, but not aContractor. -
Relationships must have certain types. For example, all relationships in the path must be of type
EMPLOYED_BY. -
Nodes or relationships must have properties satisfying some condition. For example, all relationships must have the property
distance > 10.
To demonstrate the utility of predicates in quantified path patterns, this section considers an example of finding the shortest path by physical distance and compares that to the results yielded by using the SHORTEST keyword. The graph in this example continues with Station nodes, but adds both a geospatial location property to the Stations, as well as LINK relationships with a distance property representing the distance between pairs of Stations:
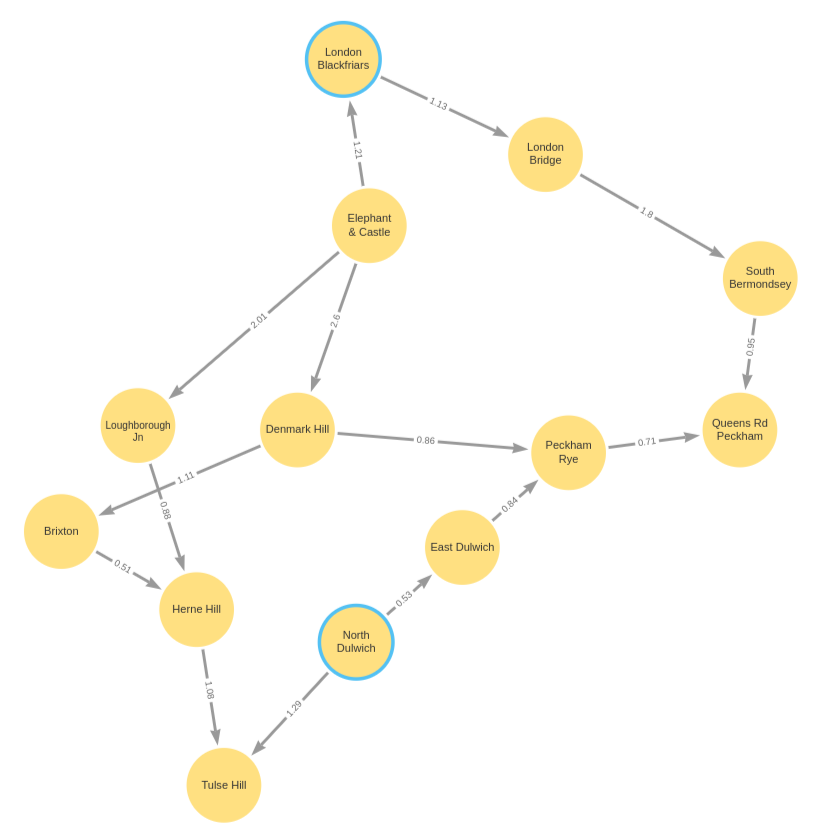
CREATE (lbg:Station {name: "London Bridge"}),
(bfr:Station {name: "London Blackfriars"}),
(eph:Station {name: "Elephant & Castle"}),
(dmk:Station {name: "Denmark Hill"}),
(pmr:Station {name: "Peckham Rye"}),
(qrp:Station {name: "Queens Rd Peckham"}),
(sbm:Station {name: "South Bermondsey"}),
(lgj:Station {name: "Loughborough Jn"}),
(hnh:Station {name: "Herne Hill"}),
(tuh:Station {name: "Tulse Hill"}),
(ndl:Station {name: "North Dulwich"}),
(edw:Station {name: "East Dulwich"}),
(brx:Station {name: "Brixton"})
SET lbg.location = point({longitude: -0.08609, latitude: 51.50502}),
bfr.location = point({longitude: -0.10333, latitude: 51.51181}),
eph.location = point({longitude: -0.09873, latitude: 51.49403}),
dmk.location = point({longitude: -0.08936, latitude: 51.46820}),
pmr.location = point({longitude: -0.06941, latitude: 51.47003}),
qrp.location = point({longitude: -0.05731, latitude: 51.47357}),
sbm.location = point({longitude: -0.05468, latitude: 51.48814}),
lgj.location = point({longitude: -0.10218, latitude: 51.46630}),
hnh.location = point({longitude: -0.10229, latitude: 51.45331}),
tuh.location = point({longitude: -0.10508, latitude: 51.43986}),
ndl.location = point({longitude: -0.08792, latitude: 51.45451}),
edw.location = point({longitude: -0.08057, latitude: 51.46149}),
brx.location = point({longitude: -0.11418, latitude: 51.46330})
CREATE (lbg)<-[:LINK {distance: 1.13}]-(bfr),
(bfr)<-[:LINK {distance: 1.21}]-(eph),
(eph)-[:LINK {distance: 2.6}]->(dmk),
(dmk)-[:LINK {distance: 0.86}]->(pmr),
(pmr)-[:LINK {distance: 0.71}]->(qrp),
(qrp)<-[:LINK {distance: 0.95}]-(sbm),
(sbm)<-[:LINK {distance: 1.8}]-(lbg),
(lgj)-[:LINK {distance: 0.88}]->(hnh),
(hnh)-[:LINK {distance: 1.08}]->(tuh),
(tuh)<-[:LINK {distance: 1.29}]-(ndl),
(ndl)-[:LINK {distance: 0.53}]->(edw),
(edw)-[:LINK {distance: 0.84}]->(pmr),
(eph)-[:LINK {distance: 2.01}]->(lgj),
(dmk)-[:LINK {distance: 1.11}]->(brx),
(brx)-[:LINK {distance: 0.51}]->(hnh)
The following query finds the path length and total distance for ALL SHORTEST paths between London Blackfriars to North Dulwich:
MATCH (bfr:Station {name: 'London Blackfriars'}),
(ndl:Station {name: 'North Dulwich'})
MATCH p = ALL SHORTEST (bfr)-[:LINK]-+(ndl)
RETURN [n in nodes(p) | n.name] AS stops,
length(p) as stopCount,
reduce(acc = 0, r in relationships(p) | round(acc + r.distance, 2)) AS distance
╒═══════════════════════════════════════════════════════════════════════════════════════════════════════════╤═════════╤════════╕ │stops │stopCount│distance│ ╞═══════════════════════════════════════════════════════════════════════════════════════════════════════════╪═════════╪════════╡ │["London Blackfriars", "Elephant & Castle", "Loughborough Jn", "Herne Hill", "Tulse Hill", "North Dulwich"]│5 │6.47 │ ├───────────────────────────────────────────────────────────────────────────────────────────────────────────┼─────────┼────────┤ │["London Blackfriars", "Elephant & Castle", "Denmark Hill", "Peckham Rye", "East Dulwich", "North Dulwich"]│5 │6.04 │ └───────────────────────────────────────────────────────────────────────────────────────────────────────────┴─────────┴────────┘
Shortest paths
The Cypher® keyword SHORTEST is used to find variations of the shortest paths between nodes. This includes the ability to look for the shortest, second-shortest (and so on) paths, all available shortest paths, and groups of paths containing the same pattern length. The ANY keyword, which can be used to test the reachability of nodes from a given node(s), is also explained, as is how to apply filters in queries using SHORTEST.

Note on Cypher and GDS shortest paths
Both Cypher and Neo4j´s Graph Data Science (GDS) library can be used to find variations of the shortest paths between nodes.
Use Cypher if:
-
You need to specify complex graph navigation via quantified path patterns.
-
Creating a graph projection takes too long.
-
GDS is not available in your instance, or the size of the GDS projection is too large for your instance.
Use GDS if:
To read more about the shortest path algorithms included in the GDS library, see GDS Graph algorithms → Path finding.
SHORTEST k
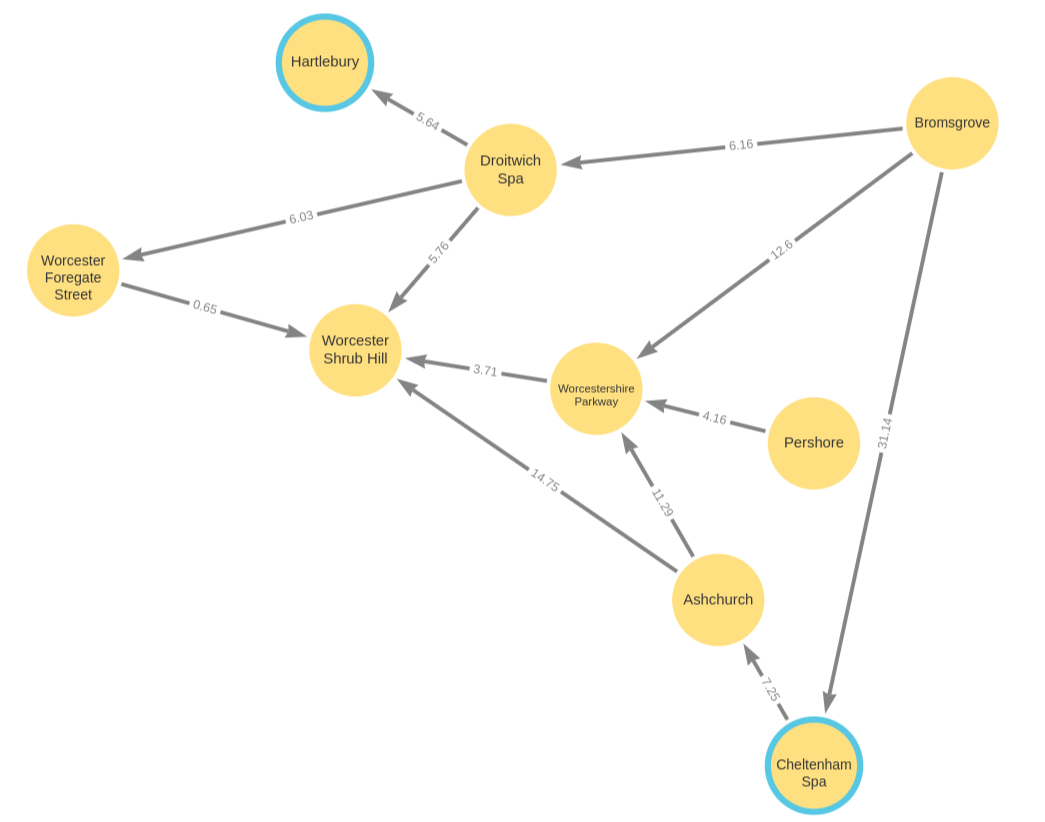
The paths matched by a path pattern can be restricted to only the shortest (by number of hops) by including the keyword SHORTEST k, where k is the number of paths to match.
MATCH p = SHORTEST 1 (wos:Station)-[:LINK]-+(bmv:Station) WHERE wos.name = "Worcester Shrub Hill" AND bmv.name = "Bromsgrove" RETURN p
╒════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════╕
│p │
╞════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════╡
│(:Station {name: "Worcester Shrub Hill"})<-[:LINK {distance: 5.76}]-(:Station {name: "Droitwich Spa"})<-[:LINK {distance: 6.16}]-(:Station {name: "Bromsgrove"})│
└────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────┘
Although the query returned a single result, there are in fact two paths that are tied for shortest:
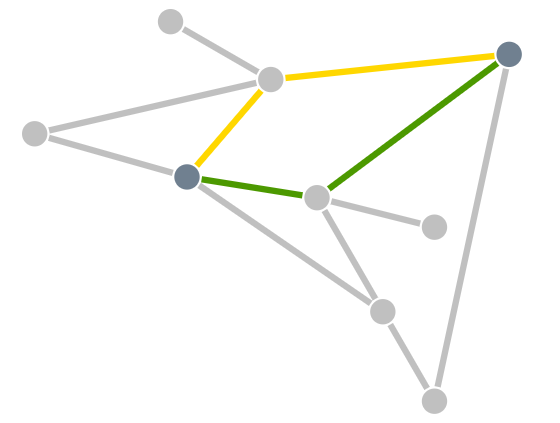
Because 1 was specified in SHORTEST, only one of the paths is returned. Which one is returned is non-deterministic.
If instead SHORTEST 2 is specified, all shortest paths in this example would be returned, and the result would be deterministic.
ALL SHORTEST
To return all paths that are tied for shortest length, use the keywords ALL SHORTEST:
MATCH p = ALL SHORTEST (wos:Station)-[:LINK]-+(bmv:Station) WHERE wos.name = "Worcester Shrub Hill" AND bmv.name = "Bromsgrove" RETURN p
╒═════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════╕
│p │
╞═════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════╡
│(:Station {name: "Worcester Shrub Hill"})<-[:LINK {distance: 5.76}]-(:Station {name: "Droitwich Spa"})<-[:LINK {distance: 6.16}]-(:Station {name: "Bromsgrove"}) │
├─────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────┤
│(:Station {name: "Worcester Shrub Hill"})<-[:LINK {distance: 3.71}]-(:Station {name: "Worcestershire Parkway"})<-[:LINK {distance: 12.6}]-(:Station {name: "Bromsgrove"})│
└─────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────┘
SHORTEST k GROUPS
To return all paths that are tied for first, second, and so on up to the kth shortest length, use SHORTEST k GROUPS.
MATCH p = SHORTEST 2 GROUPS (wos:Station)-[:LINK]-+(bmv:Station) WHERE wos.name = "Worcester Shrub Hill" AND bmv.name = "Bromsgrove" RETURN [n in nodes(p) | n.name] AS stops, length(p) AS pathLength
╒════════════════════════════════════════════════════════════════════════════════════╤══════════╕ │stops │pathLength│ ╞════════════════════════════════════════════════════════════════════════════════════╪══════════╡ │["Worcester Shrub Hill", "Droitwich Spa", "Bromsgrove"] │2 │ ├────────────────────────────────────────────────────────────────────────────────────┼──────────┤ │["Worcester Shrub Hill", "Worcestershire Parkway", "Bromsgrove"] │2 │ ├────────────────────────────────────────────────────────────────────────────────────┼──────────┤ │["Worcester Shrub Hill", "Ashchurch", "Cheltenham Spa", "Bromsgrove"] │3 │ ├────────────────────────────────────────────────────────────────────────────────────┼──────────┤ │["Worcester Shrub Hill", "Worcester Foregate Street", "Droitwich Spa", "Bromsgrove"]│3 │ ├────────────────────────────────────────────────────────────────────────────────────┼──────────┤ │["Worcester Shrub Hill", "Ashchurch", "Worcestershire Parkway", "Bromsgrove"] │3 │ └────────────────────────────────────────────────────────────────────────────────────┴──────────┘
ANY
The ANY keyword can be used to test the reachability of nodes from a given node(s). It returns the same as SHORTEST 1, but by using the ANY keyword the intent of the query is clearer. For example, the following query shows that there exists a route from Pershore to Bromsgrove where the distance between each pair of stations is less than 10 miles:
MATCH path = ANY
(:Station {name: 'Pershore'})-[l:LINK WHERE l.distance < 10]-+(b:Station {name: 'Bromsgrove'})
RETURN [r IN relationships(path) | r.distance] AS distances
╒════════════════════════╕ │distances │ ╞════════════════════════╡ │[4.16, 3.71, 5.76, 6.16]│ └────────────────────────┘
Partitions
When there are multiple start or end nodes matching a path pattern, the matches are partitioned into distinct pairs of start and end nodes prior to selecting the shortest paths; a partition is one distinct pair of start node and end node. The selection of shortest paths is then done from all paths that join the start and end node of a given partition. The results are then formed from the union of all the shortest paths found for each partition.
For example, if the start nodes of matches are bound to either Droitwich Spa or Hartlebury, and the end nodes are bound to either Ashchurch or Cheltenham Spa, there will be four distinct pairs of start and end nodes, and therefore four partitions:
| Start node | End node |
|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
The following query illustrates how these partitions define the sets of results within which the shortest paths are selected. It uses a pair of UNWIND clauses to generate a Cartesian product of the names of the Stations (all possible pairs of start node and end node), followed by the MATCH clause to find the shortest two groups of paths for each pair of distinct start and end Stations:
UNWIND ["Droitwich Spa", "Hartlebury"] AS a
UNWIND ["Ashchurch", "Cheltenham Spa"] AS b
MATCH SHORTEST 2 GROUPS (o:Station {name: a})-[l]-+(d:Station {name: b})
RETURN o.name AS start, d.name AS end,
size(l) AS pathLength, count(*) AS numPaths
ORDER BY start, end, pathLength
╒═══════════════╤════════════════╤══════════╤════════╕ │start │end │pathLength│numPaths│ ╞═══════════════╪════════════════╪══════════╪════════╡ │"Droitwich Spa"│"Ashchurch" │2 │1 │ ├───────────────┼────────────────┼──────────┼────────┤ │"Droitwich Spa"│"Ashchurch" │3 │4 │ ├───────────────┼────────────────┼──────────┼────────┤ │"Droitwich Spa"│"Cheltenham Spa"│2 │1 │ ├───────────────┼────────────────┼──────────┼────────┤ │"Droitwich Spa"│"Cheltenham Spa"│3 │1 │ ├───────────────┼────────────────┼──────────┼────────┤ │"Hartlebury" │"Ashchurch" │3 │1 │ ├───────────────┼────────────────┼──────────┼────────┤ │"Hartlebury" │"Ashchurch" │4 │4 │ ├───────────────┼────────────────┼──────────┼────────┤ │"Hartlebury" │"Cheltenham Spa"│3 │1 │ ├───────────────┼────────────────┼──────────┼────────┤ │"Hartlebury" │"Cheltenham Spa"│4 │1 │ └───────────────┴────────────────┴──────────┴────────┘
Pre-filters and post-filters
The position of a filter in a shortest path query will affect whether it is applied before or after selecting the shortest paths. To see the difference, first consider a query that returns the shortest path from Hartlebury to Cheltenham Spa:
MATCH SHORTEST 1
(:Station {name: 'Hartlebury'})
(()--(n))+
(:Station {name: 'Cheltenham Spa'})
RETURN [stop in n[..-1] | stop.name] AS stops
╒═══════════════════════════════╕ │stops │ ╞═══════════════════════════════╡ │["Droitwich Spa", "Bromsgrove"]│ └───────────────────────────────┘
Note that n[..-1] is a slicing operation that returns all elements of n except the last. If instead, the query uses a WHERE clause at the MATCH level to filter out routes that go via Bromsgrove, the filtering is applied after the shortest paths are selected. This results in the only solution being removed, and no results being returned:
MATCH SHORTEST 1
(:Station {name: 'Hartlebury'})
(()--(n:Station))+
(:Station {name: 'Cheltenham Spa'})
WHERE none(stop IN n[..-1] WHERE stop.name = 'Bromsgrove')
RETURN [stop in n[..-1] | stop.name] AS stops
(no changes, no records)
There are two ways to turn a post-filter without solutions into a pre-filter that returns solutions. One is to inline the predicate into the path pattern:
MATCH SHORTEST 1
(:Station {name: 'Hartlebury'})
(()--(n:Station WHERE n.name <> 'Bromsgrove'))+
(:Station {name: 'Cheltenham Spa'})
RETURN [stop in n[..-1] | stop.name] AS stops
╒══════════════════════════════════════════════════════╕ │stops │ ╞══════════════════════════════════════════════════════╡ │["Droitwich Spa", "Worcester Shrub Hill", "Ashchurch"]│ └──────────────────────────────────────────────────────┘
The shortest journey that avoids Bromsgrove is now returned.
An alternative is to wrap the path pattern and filter in parentheses (leaving the SHORTEST keyword on the outside):
MATCH SHORTEST 1
( (:Station {name: 'Hartlebury'})
(()--(n:Station))+
(:Station {name: 'Cheltenham Spa'})
WHERE none(stop IN n[..-1] WHERE stop.name = 'Bromsgrove') )
RETURN [stop in n[..-1] | stop.name] AS stops
╒══════════════════════════════════════════════════════╕ │stops │ ╞══════════════════════════════════════════════════════╡ │["Droitwich Spa", "Worcester Shrub Hill", "Ashchurch"]│ └──────────────────────────────────────────────────────┘
Pre-filter with a path variable
The previous section showed how to apply a filter before the shortest path selection by the use of parentheses. Placing a path variable declaration before the shortest path keywords, however, places it outside the scope of the parentheses. To reference a path variable in a pre-filter, it has to be declared inside the parentheses.
To illustrate, consider this example that returns all shortest paths from Hartlebury to each of the other Stations:
MATCH p = SHORTEST 1 (:Station {name: 'Hartlebury'})--+(b:Station)
RETURN b.name AS destination, length(p) AS pathLength
ORDER BY pathLength, destination
╒═══════════════════════════╤══════════╕ │destination │pathLength│ ╞═══════════════════════════╪══════════╡ │"Droitwich Spa" │1 │ ├───────────────────────────┼──────────┤ │"Bromsgrove" │2 │ ├───────────────────────────┼──────────┤ │"Worcester Foregate Street"│2 │ ├───────────────────────────┼──────────┤ │"Worcester Shrub Hill" │2 │ ├───────────────────────────┼──────────┤ │"Ashchurch" │3 │ ├───────────────────────────┼──────────┤ │"Cheltenham Spa" │3 │ ├───────────────────────────┼──────────┤ │"Worcestershire Parkway" │3 │ ├───────────────────────────┼──────────┤ │"Pershore" │4 │ └───────────────────────────┴──────────┘
If the query is altered to only include routes that have an even number of stops, adding a WHERE clause at the MATCH level will not work, because it would be a post-filter. It would return the results of the previous query with all routes with an odd number of stops removed:
MATCH p = SHORTEST 1 (:Station {name: 'Hartlebury'})--+(b:Station)
WHERE length(p) % 2 = 0
RETURN b.name AS destination, length(p) AS pathLength
ORDER BY pathLength, destination
╒═══════════════════════════╤══════════╕ │destination │pathLength│ ╞═══════════════════════════╪══════════╡ │"Bromsgrove" │2 │ ├───────────────────────────┼──────────┤ │"Worcester Foregate Street"│2 │ ├───────────────────────────┼──────────┤ │"Worcester Shrub Hill" │2 │ ├───────────────────────────┼──────────┤ │"Pershore" │4 │ └───────────────────────────┴──────────┘
To move the predicate to a pre-filter, the path variable should be referenced from within the parentheses, and the shortest routes with an even number of stops will be returned for all the destinations:
MATCH SHORTEST 1
(p = (:Station {name: 'Hartlebury'})--+(b:Station)
WHERE length(p) % 2 = 0 )
RETURN b.name AS destination, length(p) AS pathLength
ORDER BY pathLength, destination
╒═══════════════════════════╤══════════╕ │destination │pathLength│ ╞═══════════════════════════╪══════════╡ │"Bromsgrove" │2 │ ├───────────────────────────┼──────────┤ │"Worcester Foregate Street"│2 │ ├───────────────────────────┼──────────┤ │"Worcester Shrub Hill" │2 │ ├───────────────────────────┼──────────┤ │"Ashchurch" │4 │ ├───────────────────────────┼──────────┤ │"Cheltenham Spa" │4 │ ├───────────────────────────┼──────────┤ │"Droitwich Spa" │4 │ ├───────────────────────────┼──────────┤ │"Pershore" │4 │ ├───────────────────────────┼──────────┤ │"Worcestershire Parkway" │4 │ └───────────────────────────┴──────────┘
Planning shortest path queries
This section describes the operators used when planning shortest path queries. For readers not familiar with Cypher execution plans and operators, it is recommended to first read the section Understanding execution plans.
There are two operators used to plan SHORTEST queries:
-
StatefulShortestPath(All)- uses a unidirectional breadth-first search algorithm to find shortest paths from a previously matched start node to an end node that has not yet been matched. -
StatefulShortestPath(Into)- uses a bidirectional breadth-first search (BFS) algorithm, where two simultaneous BFS invocations are performed, one from the left boundary node and one from the right boundary node.
StatefulShortestPath(Into) is used by the planner when both boundary nodes in the shortest path are estimated to match at most one node each. Otherwise, StatefulShortestPath(All) is used.
For example, the planner estimates that the left boundary node in the below query will match one node, and the right boundary node will match five nodes, and chooses to expand from the left boundary node. Using StatefulShortestPath(Into) would require five bidirectional breadth-first search (BFS) invocations, whereas StatefulShortestPath(All) would require only one unidirectional BFS invocation. As a result, the query will use StatefulShortestPath(All).
Non-linear patterns
Cypher® can be used to express non-linear patterns, either by equijoins (an operation in which more than one node relationship in a path is the same) or by more complicated graph patterns consisting of multiple path patterns.
Equijoins
An equijoin is an operation on paths that requires more than one of the nodes or relationships of the paths to be the same. The equality between the nodes or relationships is specified by declaring the same variable in multiple node patterns or relationship patterns. An equijoin allows cycles to be specified in a path pattern.
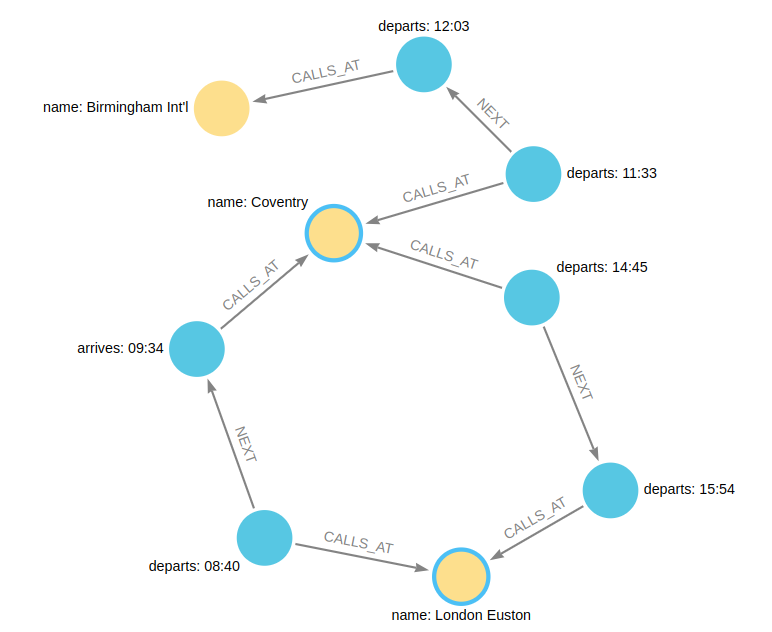
CREATE (bhi:Station {name: 'Birmingham International'}),
(cov:Station {name: 'Coventry'}),
(eus:Station {name: 'London Euston'}),
(bhi)<-[:CALLS_AT]-(s1:Stop {departs: time('12:03')}),
(cov)<-[:CALLS_AT]-(s2:Stop {departs: time('11:33')})-[:NEXT]->(s1),
(eus)<-[:CALLS_AT]-(s3:Stop {departs: time('15:54')}),
(cov)<-[:CALLS_AT]-(s4:Stop {departs: time('14:45')})-[:NEXT]->(s3),
(cov)<-[:CALLS_AT]-(s5:Stop {departs: time('09:34')}),
(eus)<-[:CALLS_AT]-(s6:Stop {departs: time('08:40')})-[:NEXT]->(s5)
To illustrate how equijoins work, we will use the problem of finding a round trip between two Stations.
In this example scenario, a passenger starts their outbound journey at London Euston Station and ends at Coventry Station. The return journey will be the reverse order of those Stations.
The graph has three different services, two of which would compose the desired round trip, and a third which would send the passenger to Birmingham International.
The solution is the following path with a cycle:
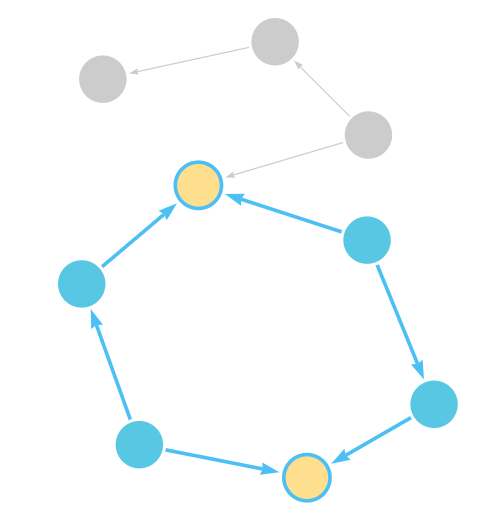
If unique properties exist on the node where the cycle "join" occurs in the path, then it is possible to repeat the node pattern with a predicate matching on the unique property. The following motif demonstrates how that can be achieved, repeating a Station node pattern with the name London Euston:

The path pattern equivalent is:
(:Station {name: 'London Euston'})<-[:CALLS_AT]-(:Stop)-[:NEXT]->(:Stop)
-[:CALLS_AT]->(:Station {name: 'Coventry'})<-[:CALLS_AT]-(:Stop)
-[:NEXT]->(:Stop)-[:CALLS_AT]->(:Station {name: 'London Euston'})
There may be cases where a unique predicate is not available. In this case, an equijoin can be used to define the desired cycle by using a repeated node variable. In the current example, if you declare the same node variable n in both the first and last node patterns, then the node patterns must match the same node:

Putting this path pattern with an equijoin in a query, the times of the outbound and return journeys can be returned:
MATCH (n:Station {name: 'London Euston'})<-[:CALLS_AT]-(s1:Stop)
-[:NEXT]->(s2:Stop)-[:CALLS_AT]->(:Station {name: 'Coventry'})
<-[:CALLS_AT]-(s3:Stop)-[:NEXT]->(s4:Stop)-[:CALLS_AT]->(n)
RETURN s1.departs+'-'+s2.departs AS outbound,
s3.departs+'-'+s4.departs AS `return`
Graph patterns
In addition to the single path patterns, multiple path patterns can be combined in a comma-separated list to form a graph pattern. In a graph pattern, each path pattern is matched separately, and where node variables are repeated in the separate path patterns, the solutions are reduced via equijoins. If there are no equijoins between the path patterns, the result is a Cartesian product between the separate solutions.
The benefit of joining multiple path patterns in this way is that it allows the specification of more complex patterns than the linear paths allowed by a single path pattern. To illustrate this, another example drawn from the railway model will be used. In this example, a passenger is traveling from Starbeck to Huddersfield, changing trains at Leeds. To get to Leeds from Starbeck, the passenger can take a direct service that stops at all stations on the way. However, there is an opportunity to change at one of the stations (Harrogate) on the way to Leeds, and catch an express train, which may enable the passenger to catch an earlier train leaving from Leeds, reducing the overall journey time.
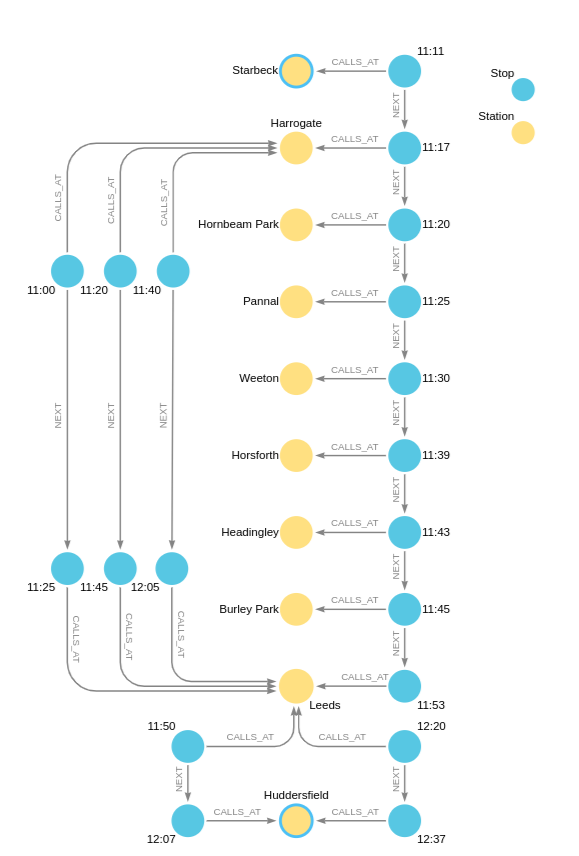
CREATE (hgt:Station {name: 'Harrogate'}), (lds:Station {name: 'Leeds'}),
(sbe:Station {name: 'Starbeck'}), (hbp:Station {name: 'Hornbeam Park'}),
(wet:Station {name: 'Weeton'}), (hrs:Station {name: 'Horsforth'}),
(hdy:Station {name: 'Headingley'}), (buy:Station {name: 'Burley Park'}),
(pnl:Station {name: 'Pannal'}), (hud:Station {name: 'Huddersfield'}),
(s9:Stop {arrives: time('11:53')}),
(s8:Stop {arrives: time('11:44'), departs: time('11:45')}),
(s7:Stop {arrives: time('11:40'), departs: time('11:43')}),
(s6:Stop {arrives: time('11:38'), departs: time('11:39')}),
(s5:Stop {arrives: time('11:29'), departs: time('11:30')}),
(s4:Stop {arrives: time('11:24'), departs: time('11:25')}),
(s3:Stop {arrives: time('11:19'), departs: time('11:20')}),
(s2:Stop {arrives: time('11:16'), departs: time('11:17')}),
(s1:Stop {departs: time('11:11')}), (s21:Stop {arrives: time('11:25')}),
(s211:Stop {departs: time('11:00')}), (s10:Stop {arrives: time('11:45')}),
(s101:Stop {departs: time('11:20')}), (s11:Stop {arrives: time('12:05')}),
(s111:Stop {departs: time('11:40')}), (s12:Stop {arrives: time('12:07')}),
(s121:Stop {departs: time('11:50')}), (s13:Stop {arrives: time('12:37')}),
(s131:Stop {departs: time('12:20')}),
(lds)<-[:CALLS_AT]-(s9), (buy)<-[:CALLS_AT]-(s8)-[:NEXT]->(s9),
(hdy)<-[:CALLS_AT]-(s7)-[:NEXT]->(s8), (hrs)<-[:CALLS_AT]-(s6)-[:NEXT]->(s7),
(wet)<-[:CALLS_AT]-(s5)-[:NEXT]->(s6), (pnl)<-[:CALLS_AT]-(s4)-[:NEXT]->(s5),
(hbp)<-[:CALLS_AT]-(s3)-[:NEXT]->(s4), (hgt)<-[:CALLS_AT]-(s2)-[:NEXT]->(s3),
(sbe)<-[:CALLS_AT]-(s1)-[:NEXT]->(s2), (lds)<-[:CALLS_AT]-(s21), (hgt)<-[:CALLS_AT]-(s211)-[:NEXT]->(s21), (lds)<-[:CALLS_AT]-(s10), (hgt)<-[:CALLS_AT]-(s101)-[:NEXT]->(s10), (lds)<-[:CALLS_AT]-(s11), (hgt)<-[:CALLS_AT]-(s111)-[:NEXT]->(s11), (hud)<-[:CALLS_AT]-(s12), (lds)<-[:CALLS_AT]-(s121)-[:NEXT]->(s12), (hud)<-[:CALLS_AT]-(s13), (lds)<-[:CALLS_AT]-(s131)-[:NEXT]->(s13)
The solution to the problem assembles a set of path patterns matching the following three parts: the stopping service; the express service; and the final leg of the journey from Leeds to Huddersfield. Each changeover, from stopping to express service and from express to onward service, has to respect the fact that the arrival time of a previous leg has to be before the departure time of the next leg. This will be encoded in a single WHERE clause.
The following visualizes the three legs with different colors, and identifies the node variables used to create the equijoins and anchoring:
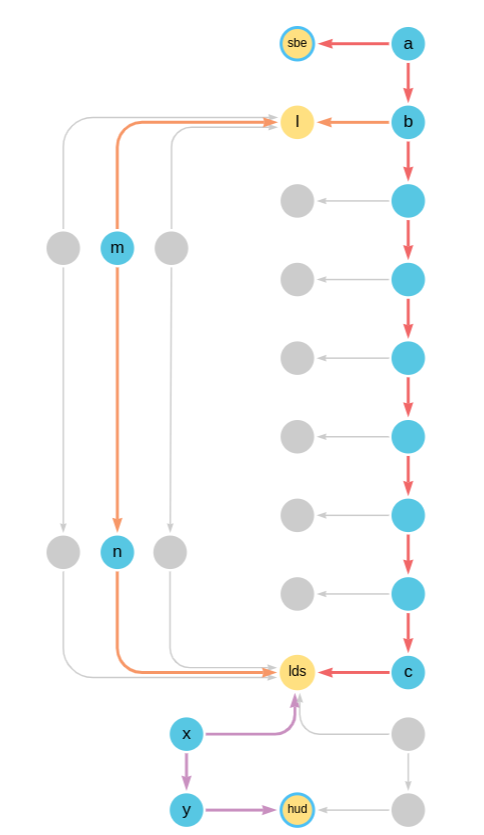
For the stopping service, it is assumed that the station the passenger needs to change at is unknown. As a result, the pattern needs to match a variable number of stops before and after the Stop b, the Stop that calls at the changeover station l. This is achieved by placing the quantified relationship -[:NEXT]->* on each side of node b. The ends of the path also needs to be anchored at a Stop departing from Starbeck at 11:11, as well as at a Stop calling at Leeds:
(:Station {name: 'Starbeck'})<-[:CALLS_AT]-
(a:Stop {departs: time('11:11')})-[:NEXT]->*(b)-[:NEXT]->*
(c:Stop)-[:CALLS_AT]->(lds:Station {name: 'Leeds'})
For the express service, the ends of the path are anchored at the stop b and Leeds station, which lds will be bound to by the first leg. Although in this particular case there are only two stops on the service, a more general pattern that can match any number of stops is used:
(b)-[:CALLS_AT]->(l:Station)<-[:CALLS_AT]-(m:Stop)-[:NEXT]->* (n:Stop)-[:CALLS_AT]->(lds)
Note that as Cypher only allows a relationship to be traversed once in a given match for a graph pattern, the first and second legs are guaranteed to be different train services. (See relationship uniqueness for more details.) Similarly, another quantified relationship that bridges the stops calling at Leeds station and Huddersfield station is added:
(lds)<-[:CALLS_AT]-(x:Stop)-[:NEXT]->*(y:Stop)-[:CALLS_AT]->
(:Station {name: 'Huddersfield'})
The other node variables are for the WHERE clause or for returning data. Putting this together, the resulting query returns the earliest arrival time achieved by switching to an express service:
MATCH (:Station {name: 'Starbeck'})<-[:CALLS_AT]-
(a:Stop {departs: time('11:11')})-[:NEXT]->*(b)-[:NEXT]->*
(c:Stop)-[:CALLS_AT]->(lds:Station {name: 'Leeds'}),
(b)-[:CALLS_AT]->(l:Station)<-[:CALLS_AT]-(m:Stop)-[:NEXT]->*
(n:Stop)-[:CALLS_AT]->(lds),
(lds)<-[:CALLS_AT]-(x:Stop)-[:NEXT]->*(y:Stop)-[:CALLS_AT]->
(:Station {name: 'Huddersfield'})
WHERE b.arrives < m.departs AND n.arrives < x.departs
RETURN a.departs AS departs,
l.name AS changeAt,
m.departs AS changeDeparts,
y.arrives AS arrives
ORDER BY y.arrives LIMIT 1
╒═══════════╤═══════════╤═════════════╤═══════════╕ │departs │changeAt │changeDeparts│arrives │ ╞═══════════╪═══════════╪═════════════╪═══════════╡ │"11:11:00Z"│"Harrogate"│"11:20:00Z" │"12:07:00Z"│ └───────────┴───────────┴─────────────┴───────────┘
Syntax and semantics
Node patterns
nodePattern ::= "(" [ nodeVariable ] [ labelExpression ]
[ propertyKeyValueExpression ] [ elementPatternWhereClause] ")"
elementPatternWhereClause ::= "WHERE" booleanExpression
Relationship patterns
relationshipPattern ::= fullPattern | abbreviatedRelationship
fullPattern ::=
"<-[" patternFiller "]-"
| "-[" patternFiller "]->"
| "-[" patternFiller "]-"
abbreviatedRelationship ::= "<--" | "--" | "-->"
patternFiller ::= [ relationshipVariable ] [ typeExpression ]
[ propertyKeyValueExpression ] [ elementPatternWhereClause ]
elementPatternWhereClause ::= "WHERE" booleanExpression
Label expressions
labelExpression ::= ":" labelTerm
labelTerm ::=
labelIdentifier
| labelTerm "&" labelTerm
| labelTerm "|" labelTerm
| "!" labelTerm
| "%"
| "(" labelTerm ")"
Rules
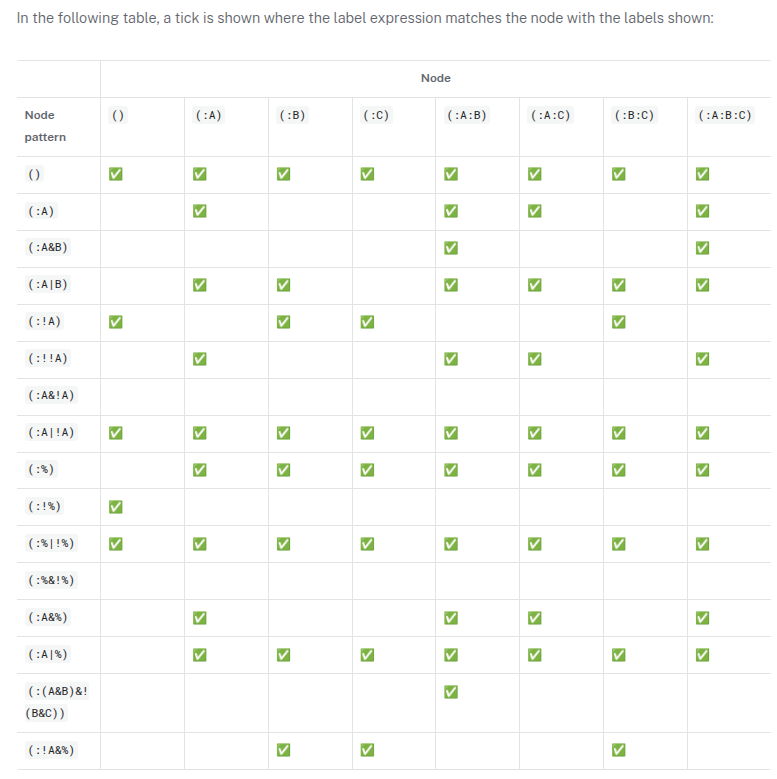
The following table lists the symbols used in label expressions:
| Symbol | Description | Precedence |
|---|---|---|
|
|
Wildcard. Evaluates to |
|
|
|
Contained expression is evaluated before evaluating the outer expression the group is contained in. |
1 (highest) |
|
|
Negation |
2 |
|
|
Conjunction |
3 |
|
|
Disjunction |
4 (lowest) |
Associativity is left-to-right.
Property key-value expressions
propertyKeyValueExpression ::=
"{" propertyKeyValuePairList "}"
propertyKeyValuePairList ::=
propertyKeyValuePair [ "," propertyKeyValuePair ]
propertyKeyValuePair ::= propertyName ":" valueExpression
Path patterns
A path pattern is the top level pattern that is matched against paths in a graph.
pathVariableDeclaration ::= pathVariable "="
pathPatternExpression ::=
{ parenthesizedPathPatternExpression | pathPatternPhrase }
parenthesizedPathPatternExpression ::=
"("
[ subpathVariableDeclaration ]
pathPatternExpression
[ parenthesizedPathPatternWhereClause ]
")"
subpathVariableDeclaration ::= pathVariable "="
pathPatternPhrase ::= [{ simplePathPattern | quantifiedPathPattern }]+
simplePathPattern ::= nodePattern
[ { relationshipPattern | quantifiedRelationship } nodePattern ]*
parenthesizedPathPatternWhereClause ::= "WHERE" booleanExpression
Quantified path patterns
A quantified path pattern represents a path pattern repeated a number of times in a given range. It is composed of a path pattern, representing the path section to be repeated, followed by a quantifier, constraining the number of repetitions between a lower bound and an upper bound.
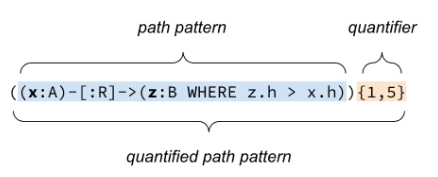
quantifiedPathPattern ::= parenthesizedPathPatternExpression quantifier fixedPath ::= nodePattern [ relationshipPattern nodePattern ]+
Quantified relationships
quantifiedRelationship ::= relationshipPattern quantifier
Quantifiers
quantifier ::= "*" | "+" | fixedQuantifier | generalQuantifier fixedQuantifier ::= "{" unsignedDecimalInteger "}" generalQuantifier ::= "{" lowerBound "," upperBound "}" lowerBound ::= unsignedDecimalInteger upperBound ::= unsignedDecimalInteger unsignedDecimalInteger ::= [0-9]+
Rules
The absence of an upper bound in the general quantifier syntax means there is no upper bound. The following table shows variants of the quantifier syntax and their canonical form:
| Variant | Canonical form | Description |
|---|---|---|
|
|
|
Between m and n iterations. |
|
|
|
1 or more iterations. |
|
|
|
0 or more iterations. |
|
|
|
Exactly n iterations. |
|
|
|
m or more iterations. |
|
|
|
Between 0 and n iterations. |
|
|
|
0 or more iterations. |
Variable-length relationships
varLengthRelationship ::=
"<-[" varLengthFiller "]-"
| "-[" varLengthFiller "]->"
| "-[" varLengthFiller "]-"
varLengthFiller ::= [ relationshipVariable ] [ varLengthTypeExpression ]
[ varLengthQuantifier ] [ propertyKeyValueExpression ]
varLengthTypeExpression ::= ":" varLengthTypeTerm
varLengthTypeTerm ::=
typeIdentifier
| varLengthTypeTerm "|" varLengthTypeTerm
varLengthQuantifier ::= varLengthVariable | varLengthFixed
varLengthVariable ::= "*" [ [ lowerBound ] ".." [ upperBound ] ]
varLengthFixed ::= "*" fixedBound
fixedBound ::= unsignedDecimalInteger
lowerBound ::= unsignedDecimalInteger
upperBound ::= unsignedDecimalInteger
unsignedDecimalInteger ::= [0-9]+
Rules
The following table shows variants of the variable-length quantifier syntax and their equivalent quantifier form (the form used by quantified path patterns):
| Variant | Description | Quantified relationship equivalent | Quantified path pattern equivalent |
|---|---|---|---|
|
|
1 or more iterations. |
|
|
|
|
Exactly n iterations. |
|
|
|
|
Between m and n iterations. |
|
|
|
|
m or more iterations. |
|
|
|
|
0 or more iterations. |
|
|
|
|
Between 1 and n iterations. |
|
|
|
|
Between 0 and n iterations. |
|
|
Note that * used here on its own is not the same as the Kleene star (an operator that represents zero or more repetitions), as the Kleene star has a lower bound of zero. The above table can be used to translate the quantifier used in variable-length relationships. The rules given for quantified path patterns would apply to the translation.
This table shows some examples:
| Variable-length relationship | Equivalent quantified path pattern |
|---|---|
|
|
|
|
|
|
|
|
|
Graph patterns
A graph pattern is a comma separated list of one or more path patterns. It is the top level construct provided to MATCH.
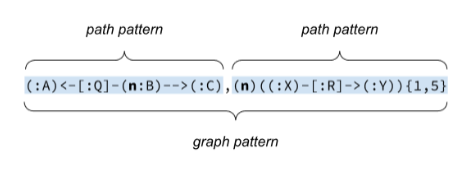
graphPattern ::= pathPattern [ "," pathPattern ]* [ graphPatternWhereClause ] graphPatternWhereClause ::= "WHERE" booleanExpression
Rules
The rules for path patterns apply to each constituent path pattern of a graph pattern.
Variable references
If a variable is declared inside a quantified path pattern, then it can be treated as a singleton only from within the quantified path pattern it was declared in. Outside of that quantified path pattern, it must be treated as a group variable.
((n)-[r]->(m WHERE r.p = m.q))+(n)-[r]->+(m WHERE all(rel in r WHERE rel.q > m.q))(n)-[r]->+(m WHERE r.p = m.q)Relationship uniqueness
A relationship can only be traversed once in a given match for a graph pattern. The same restriction doesn’t hold for nodes, which may be re-traversed any number of times in a match.
Equijoin
If a node variable is declared more than once in a path pattern, it is expressing an equijoin. This is an operation that requires that each node pattern with the same node variable be bound to the same node. For example, the following pattern refers to the same node twice with the variable a, forming a cycle:
(a)-->(b)-->(c)-->(a)The following pattern refers to the same node with variable b in different path patterns of the same graph pattern, forming a "T" shaped pattern:
(a)-->(b)-->(c), (b)-->(e)Equijoins can only be made using variables outside of quantified path patterns. The following would not be a valid equijoin:
(a)-->(b)-->(c), ((b)-->(e))+ (:X)If no equijoin exists between path patterns in a graph pattern, then a Cartesian join is formed from the sets of matches for each path pattern. An equijoin can be expressed between relationship patterns by declaring a relationship variable multiple times. However, as relationships can only be traversed once in a given match, no solutions would be returned.
Examples
The WHERE clause can refer to variables inside and outside of quantified path patterns:
(a)-->(b)-->(c), (b) ((d)-->(e))+ WHERE any(n in d WHERE n.p = a.p)An equijoin can be formed to match "H" shaped graphs:
(:A)-->(x)--(:B), (x)-[:R]->+(y), (:C)-->(y)-->(:D)With no variables in common, this graph pattern will result in a Cartesian join between the sets of matches for the two path patterns:
(a)-->(b)-->(c), ((d)-->(e))+Multiple equijoins can be formed between path patterns:
(:X)-->(a:A)-[!:R]->+(b:B)-->(:Y), (a)-[:R]->+(b)Variables declared in a previous MATCH can be referenced inside of a quantified path pattern:
MATCH (n {p = 'ABC'})
MATCH (n)-->(m:A)-->(:B), (m) (()-[r WHERE r.p <> n.p]->())+ (:C)The repetition of a relationship variable in the following yields no solutions due to Cypher enforcing relationship uniqueness within a match for a graph pattern:
MATCH ()-[r]->()-->(), ()-[r]-()Node pattern pairs
It is not valid syntax to write a pair of node patterns next to each other. For example, all of the following would raise a syntax error:
(a:A)(b:B)(a:A)(b:B)<-[r:R]-(c:C) (a:A)<--(b:B)(c:C)-->(d:C)However, the placing of pairs of node patterns next to each other is valid where it results indirectly from the expansion of quantified path patterns.
Iterations of quantified path patterns
When a quantified path pattern is expanded, the fixed path pattern contained in its parentheses is repeated and chained. This results in pairs of node patterns sitting next to each other. Take the following quantified path pattern as an example:
((x:X)<--(y:Y)){3}This is expanded by repeating the fixed path pattern (x:X)←-(y:Y) three times, with indices on the variables to show that no equijoin is implied (see equijoins for more information):
(x1:X)<--(y1:Y)(x2:X)<--(y2:Y)(x3:X)<--(y3:Y)The result is that two pairs of node patterns end up adjoining each other, (y1:Y)(x2:X) and (y2:Y)(x3:X). During the matching process, each pair of node patterns will match the same nodes, and those nodes will satisfy the conjunction of the predicates in the node patterns. For example, in the first pair both y1 and x2 will bind to the same node, and that node must have labels X and Y. This expansion and binding is depicted in the following diagram:
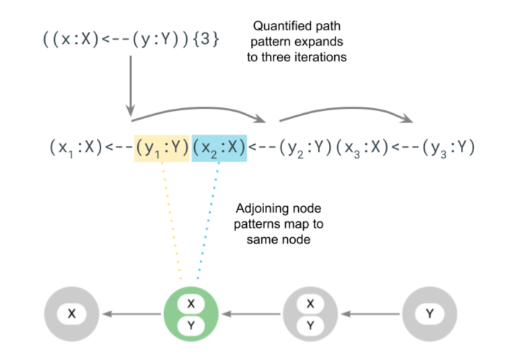
Simple path patterns and quantified path patterns
Pairs of node patterns are also generated when a simple path pattern is placed next to a quantified path. For example, consider the following path pattern:
(:A)-[:R]->(:B) ((:X)<--(:Y)){1,2}After expanding the iterations of the quantified path pattern, the right-hand node pattern (:B) adjoins the left-hand node pattern (:X). The result will match the same paths as the union of matches of the following two path patterns:
(:A)-[:R]->(:B&X)<--(:Y)(:A)-[:R]->(:B&X)<--(:Y&X)<--(:Y)If the simple path pattern is on the right of the quantified path pattern, its leftmost node (:A) adjoins the rightmost node (:Y) of the last iteration of the quantified path pattern. For example, the following:
((:X)<--(:Y)){1,2} (:A)-[:R]->(:B)will match the same paths as the union of the following two path patterns:
(:X)<--(:Y&A)-[:R]->(:B)(:X)<--(:Y&X)<--(:Y&A)-[:R]->(:B)Pairs of quantified path patterns
When two quantified path patterns adjoin, the rightmost node of the last iteration of the first pattern is merged with the leftmost node of the first iteration of the second pattern. For example, the following adjoining patterns:
((:A)-[:R]->(:B)){2} ((:X)<--(:Y)){1,2}will match the same set of paths as the union of the paths matched by these two path patterns:
(:A)-[:R]->(:B&A)-[:R]->(:B&X)<--(:Y)(:A)-[:R]->(:B&A)-[:R]->(:B&X)<--(:Y&X)<--(:Y)Zero iterations
If the quantifier allows for zero iterations of a pattern, for example {0,3}, then the 0th iteration of that pattern results in the node patterns on either side pairing up.
For example, the following path pattern:
(:X) ((a:A)-[:R]->(b:B)){0,1} (:Y)will match the same set of paths as the union of the paths matched by the following two path patterns:
(:X&Y)(:X&A)-[:R]->(:B&Y)




 浙公网安备 33010602011771号
浙公网安备 33010602011771号