Singular Value Decomposition (SVD)

Singular Value Decomposition (SVD) is a powerful mathematical technique used in linear algebra to factorize a matrix into three simpler matrices. It is widely used in dimensionality reduction, noise reduction, and recommendation systems.

---

1. Definition of SVD

---

2. Key Properties

• The singular values in Σ are always non-negative and sorted in descending order.
• The columns of U are orthonormal (i.e., they are perpendicular to each other and have unit length).
• The columns of Vare orthonormal as well.

---

3. Applications of SVD

(1) Dimensionality Reduction (PCA)

• SVD is used in Principal Component Analysis (PCA) to reduce data dimensions while preserving as much variance as possible.
• By keeping only the top k singular values, we approximate the original matrix while reducing complexity.

(2) Image Compression

• In image processing, we store only the most significant singular values and corresponding vectors, reducing the image size without losing much quality.

(3) Noise Reduction

• By keeping only the top k singular values and ignoring small ones, SVD can remove noise from data.

(4) Recommendation Systems

• Netflix, Amazon, and YouTube use SVD for collaborative filtering to make personalized recommendations.

(5) Solving Linear Systems

• SVD is used in numerical computing to solve systems of equations, especially when the matrix is singular or ill-conditioned.

---

4. Example of SVD in Python

You can compute SVD in Python using NumPy:

import numpy as np

# Create a matrix A
A = np.array([[3, 2, 2], 
              [2, 3, -2]])

# Compute SVD
U, S, Vt = np.linalg.svd(A)

# Print results
print("U matrix:\n", U)
print("Singular values:\n", S)
print("V^T matrix:\n", Vt)

This will output:

• The left singular vectors (U),
• The singular values (S),
• The right singular vectors (V^T).

---

5. Low-Rank Approximation

To approximate AAA using only the top k singular values:

This is useful in data compression and noise reduction.

---

6. Difference Between SVD and Eigen Decomposition

---

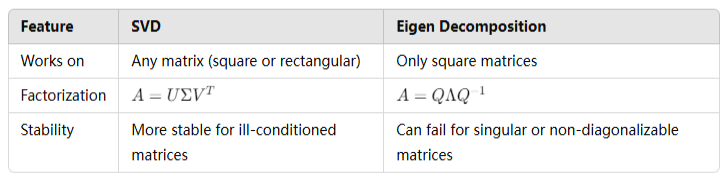
7. Summary

• SVD is a matrix factorization method that decomposes a matrix into three simpler matrices.
• Used for dimensionality reduction, image compression, noise filtering, and recommendation systems.
• Unlike eigen decomposition, SVD works for any matrix (not just square ones).
• Low-rank approximations using SVD help in data compression.