可持久化线段树

可持久化线段树

P3919 【模板】可持久化线段树 1（可持久化数组）

维护一个长度为 \(N\) 的数组，支持如下几种操作

1. 在某个历史版本上修改某一个位置上的值

2. 访问某个历史版本上的某一位置的值

此外，每进行一次操作（对于操作2，即为生成一个完全一样的版本，不作任何改动），就会生成一个新的版本。版本编号即为当前操作的编号（从1开始编号，版本0表示初始状态数组）

（\(N\):长度，\(M\):操作数，\(1 \le N,M \le 10^6\)）

显然不能开 \(M\) 棵线段树进行维护，空间会炸。

由线段树得到启发，每次修改时只会经过约 \(\mathrm{log_2} \ N\) 个节点，所以每次只需要动态开点增加一条链，改变的区间（儿子）开点，不改变的区间不变，对应到原版本位置上，记录新根节点编号即可。这样空间复杂度就是 \(O(2n-1+m \ \mathrm{log} \ n) = O(2n+m \ \mathrm{log} \ n)\)，实际开个 tree[MAXN<<5] 一般也不会爆。

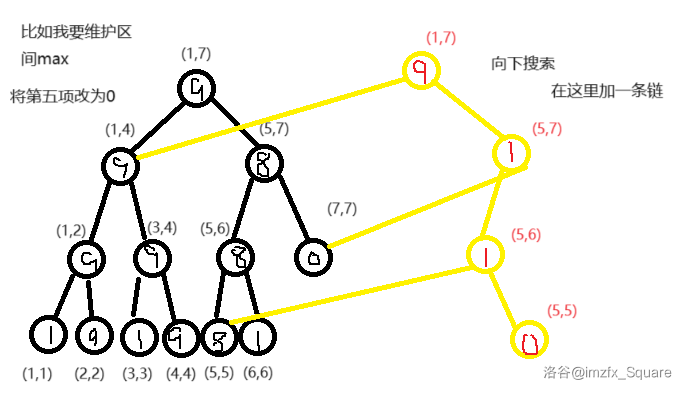
每次查询时只需要沿对应版本的根节点向下查找即可。

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+5;
struct Stree{
	int ls,rs;//左儿子 右儿子 
	int num;
	#define ls(x) tree[x].ls
	#define rs(x) tree[x].rs
	#define num(x) tree[x].num
}tree[N<<5];
int n,m,a[N],root[N<<5],cnt;
int rt,op,x,y;
int build(int l,int r){//l r 为当前节点区间
	int x=++cnt;
	if(l==r){
		num(x)=a[l];
		return x;
	}
	int mid=l+r>>1;
	ls(x)=build(l,mid);
	rs(x)=build(mid+1,r);
	return x;
}
int change(int x,int l,int r,int i,int num){//x 为原版当前节点  l r 为当前节点区间
	int y=++cnt;//y 为新版当前节点
	if(l==r){
		num(y)=num;
		return y;
	}
	int mid=l+r>>1;
	ls(y)=ls(x);
	rs(y)=rs(x);
	if(i<=mid)//更改左儿子则新建左儿子，更改右儿子则新建右儿子
		ls(y)=change(ls(x),l,mid,i,num);
	else
		rs(y)=change(rs(x),mid+1,r,i,num);
	return y;
}
int query(int x,int l,int r,int i){
	if(l==r)
		return num(x);
	int mid=l+r>>1;
	if(i<=mid)
		return query(ls(x),l,mid,i);
	else
		return query(rs(x),mid+1,r,i);
}
int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++)
		scanf("%d",&a[i]);
	root[0]=build(1,n);
	for(int i=1;i<=m;i++){
		scanf("%d%d%d",&rt,&op,&x);
		if(op==1){
			scanf("%d",&y);
			root[i]=change(root[rt],1,n,x,y);
		}else{
			printf("%d\n",query(root[rt],1,n,x));
			root[i]=root[rt];
		}
	}
	return 0;
}