*题解：P3629 [APIO2010] 巡逻

原题链接

解析

先考虑 \(K = 1\) 的情况，加一条边会连出一个环，环上所有边只需经过 \(1\) 次，这个可以利用无向图欧拉回路的判定来证明。巡逻距离最小就是要让环尽量大，所以连直径端点即可。

再来看 \(K = 2\)，由于有公共边的存在，两个环的贡献无法通过直接相加来计算。画个图发现一般情况下公共边必定走两次，非一般情况是有叶子连了两条边，这样可能公共边只走一次，然后走两遍环的另一侧会更优，但是这样必定不优于把其中一条边在该叶子处断开然后连回到点 \(1\)，所以我们只用考虑公共边走两次的情况。

考虑在定了一条路径的情况下如何去定第二条路径。考虑贡献，初始答案为 \(2n - 1\)，环上每条非公共边对答案做额外 \(-1\) 的贡献，公共边额外做 \(0\) 的贡献。所以，将在第一个环上的所有边边权置 \(1\)，其余边置 \(-1\)，问题就变成了找到树上边权最小的一条简单路径，按类似求直径的方法 dp 来求即可。为什么要置 \(1\) 而不是置 \(0\)？因为走公共边相当于把第一个环 \(-1\) 的贡献给抵消了。

那么第一条路径应该选谁呢？第一想到的肯定是直径，我们来尝试证明一下这么做是最优的：

首先钦定第一条路径的长度不小于第二条。

设路径 \(L=a \to b\) 是直径。

如果有一种更优的选法，第一条路径选了 \(l=u \to v \not= L\)，那么 \(l\) 需要与直径有公共边，否则直接选直径和 \(l\) 必定不劣。同理，第二条边 \(l_2=u_2 \to v_2\) 也需要跟直径 \(L\) 有公共边，且在长度相同的情况下， \(l_2\) 跟 \(l\) 有公共边的情况必定不优于没有公共边的情况。所以只需要考虑如图所示的这种情况：

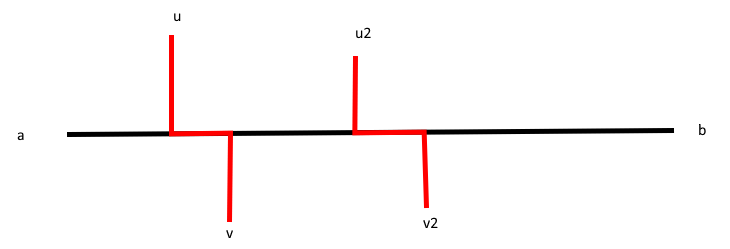
此时如果我们选取直径 \(L\) 和 \(u_2 \to v\) 作为两条路径：

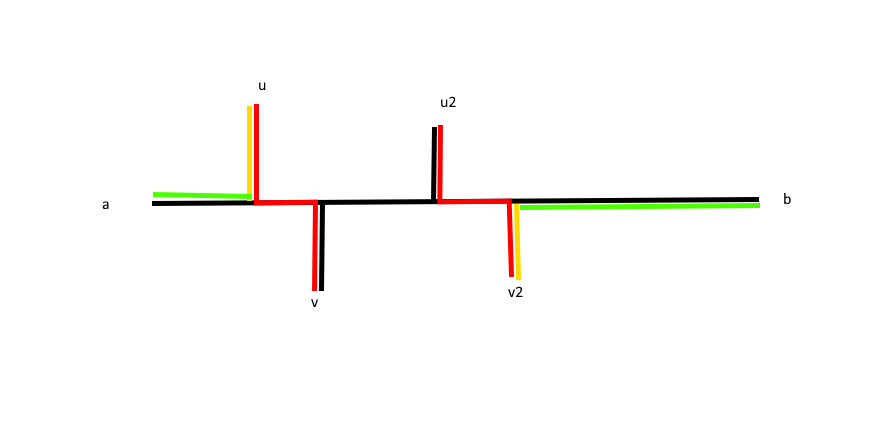
去除共有的部分后，比较绿色部分和黄色部分，显然黄色部分不可能长于绿色部分，不然 \(a \to b\) 就不是直径了。故第一条路径选直径是最优策略。

代码

方便起见可以在求第二条路径时将边权取相反数，这样就还是求最长路径。

/*
*/
#include<bits/stdc++.h>
#define eps 0.000001
using namespace std;
typedef unsigned long long ull;
typedef long long ll;
typedef pair<ll,int> pii;
const int N = 4e5 + 5,M = 3.2e4 + 5;
int head[N],to[N],nxt[N],val[N],dep[N],mxd[N][2],fae[N],f[N];
int mxpos,cnt;
void add(int u,int v){
	cnt++;
	to[cnt] = v;
	nxt[cnt] = head[u];
	val[cnt] = 1;
	head[u] = cnt;
}
void dfs(int x,int fa,int k){
	f[x] = fa;
	fae[x] = k;
	dep[x] = dep[fa] + val[k];
	mxd[x][0] = x;
	mxd[x][1] = x;
	for(int i=head[x];i;i = nxt[i])if(to[i] != fa){
		int nx = to[i];
		dfs(nx,x,i);
		int dnx = dep[mxd[nx][0]];
		if(dnx > dep[mxd[x][0]]){
			mxd[x][1] = mxd[x][0];
			mxd[x][0] = mxd[nx][0];
		}else if(dnx > dep[mxd[x][1]]){
			mxd[x][1] = mxd[nx][0];
		}
	}
	if(dep[mxd[x][0]] + dep[mxd[x][1]] - 2 * dep[x] > 
	   dep[mxd[mxpos][0]] + dep[mxd[mxpos][1]] - 2 * dep[mxpos] || !mxpos){
		mxpos = x;
	}
}
int main(){
//	freopen("in.txt","r",stdin);
//	freopen("out1.txt","w",stdout);
	ios::sync_with_stdio(false);
	cin.tie(0),cout.tie(0);
	int n,k;
	cin>>n>>k;
	for(int i=1;i<n;i++){
		int u,v;
		cin>>u>>v;
		add(u,v);
		add(v,u);
	}
	int res = (n - 1) * 2 + k;
	dfs(1,0,0);
	res -= dep[mxd[mxpos][0]] + dep[mxd[mxpos][1]] - 2 * dep[mxpos];
	if(k == 1){
		cout<<res;
		return 0;
	}
	int now = mxd[mxpos][0];
	for(int i=1;i<=cnt;i++){
		val[i] = 1;
	}
	while(now != mxpos && now){
		val[fae[now]] = val[((fae[now] - 1) ^ 1) + 1] = -1;
		now = f[now];
	}
	now = mxd[mxpos][1];
	while(now != mxpos && now){
		val[fae[now]] = val[((fae[now] - 1) ^ 1) + 1] = -1;
		now = f[now];
	}
	mxpos = 0;
	
	dfs(1,0,0);
	res -= dep[mxd[mxpos][0]] + dep[mxd[mxpos][1]] - 2 * dep[mxpos];
	cout<<res;
	return 0;
}
/*
*/