基于MATLAB的Bezier曲线曲面绘制实现
一、核心算法原理
-
Bezier曲线数学基础
-
参数方程:
![]()
其中
![]() 为Bernstein基函数,\(P_i\)为控制顶点。
为Bernstein基函数,\(P_i\)为控制顶点。 -
性质: 端点插值性:曲线通过首尾控制点 凸包性:曲线始终位于控制多边形内部 几何不变性:仅依赖控制点坐标
-
-
Bezier曲面扩展
-
张量积形式:
![]()
-
控制网格:由\((m+1)×(n+1)\)个控制点构成的矩阵
-
二、MATLAB实现代码
1. 二维Bezier曲线绘制
%% 三次Bezier曲线绘制(控制点P0-P3)
P = [0 0; 1 2; 2 -1; 3 1]; % 控制点坐标
n = size(P,1)-1; % 曲线阶数
t = linspace(0,1,100);
Bx = zeros(size(t)); By = Bx;
for k = 0:n
B = nchoosek(n,k) * t.^k .* (1-t).^(n-k);
Bx = Bx + P(k+1,1)*B;
By = By + P(k+1,2)*B;
end
figure;
plot(P(:,1), P(:,2),'go-','LineWidth',2); % 控制多边形
hold on;
plot(Bx, By,'r-','LineWidth',2); % 曲线
scatter(P(:,1), P(:,2),50,'g','filled'); % 控制点
xlabel('X'); ylabel('Y');
title('三次Bezier曲线');
grid on; axis equal;
2. 三维Bezier曲面绘制
%% 双二次Bezier曲面绘制
P = [0 0 1; 1 2 0; 2 0 1; 0 1 0; 1 1 0.5; 2 0 0; 0 2 1; 1 1 0; 2 0 1]'; % 3x3控制点矩阵
[m,n] = size(P)/3; % m行n列控制点
[u,v] = meshgrid(linspace(0,1,50));
X = zeros(size(u)); Y = X; Z = X;
for i = 1:m
for j = 1:n
% 计算Bernstein基函数
Bu = nchoosek(m-1,i-1) * u.^i .* (1-u).^(m-i);
Bv = nchoosek(n-1,j-1) * v.^j .* (1-v).^(n-j);
% 累加曲面点坐标
idx = (i-1)*n + j;
X = X + P(idx,1) * Bu * Bv;
Y = Y + P(idx,2) * Bu * Bv;
Z = Z + P(idx,3) * Bu * Bv;
end
end
figure;
surf(X,Y,Z,'EdgeColor','none');
colormap jet; shading interp;
xlabel('X'); ylabel('Y'); zlabel('Z');
title('双二次Bezier曲面');
axis equal;
三、关键优化策略
向量化计算加速
% 替代双重循环的向量化实现
Bu = nchoosek(m-1,0:m-1) * (u.^((0:m-1)')).*(1-u).^(m-(0:m-1)');
Bv = nchoosek(n-1,0:n-1) * (v.^((0:n-1)')).*(1-v).^(n-(0:n-1)');
S = Bu' * P(1:m:end,:) * Bv;
控制点动态调整
% 使用GUI滑块实时调整控制点
s = uicontrol('Style','slider','Position',[20 20 200 20],...
'Min',0,'Max',1,'Value',0.5);
set(s,'Callback',@(src,event) update_curve(src,value));
可视化增强
% 绘制控制网格
figure;
for i = 1:size(P,1)-1
plot3(P(i:i+1,1), P(i:i+1,2), P(i:i+1,3),'b-o');
hold on;
end
surf(X,Y,Z,'FaceAlpha',0.5);
四、典型应用案例
-
二次曲线绘制
P = [0 0; 1 2; 2 0]; % 三个控制点 t = 0:0.01:1; x = (1-t).^2*P(1,1) + 2*(1-t).*t*P(2,1) + t^2*P(3,1); y = (1-t).^2*P(1,2) + 2*(1-t).*t*P(2,2) + t^2*P(3,2); plot(x,y,'r',P(:,1),P(:,2),'bo-'); -
曲面变形动画
% 动态调整控制点生成变形效果 h = figure; for deg = 0:0.1:1 P(2,:) = [0.5, 0.5+sin(pi*2*deg)]; % 修改中间控制点 [X,Y,Z] = compute_bezier_surface(P); surf(X,Y,Z); drawnow; end
五、验证与调试
-
单位圆近似测试
% 用16次Bezier曲线近似单位圆 theta = linspace(0,2*pi,17); P = [cos(theta), sin(theta)]; t = linspace(0,1,1000); [X,Y] = bezier_curve(P,t); plot(X,Y,'r',P(:,1),P(:,2),'bo'); title('16次Bezier曲线圆近似'); -
曲率连续性验证
% 计算曲线曲率 [kappa,tau] = curvature(X,Y); figure; plot(t,kappa); title('曲线曲率分布');
参考代码 利用matlab,进行Bezier曲线曲面的绘制 www.youwenfan.com/contentcnn/84536.html
六、扩展功能实现
-
有理Bezier曲线
% 添加权因子w W = [1,3,1]; % 三次曲线权因子 x = sum(W.*P(:,1).*Bn_t) ./ sum(W.*Bn_t); -
曲面细分算法
% de Casteljau细分 function [P1,P2] = de_casteljau_subdivision(P,u) n = size(P,1)-1; P1 = zeros(n,2); P2 = zeros(n,2); for i = 1:n for j = 1:i P1(j,:) = (1-u)*P(j,:) + u*P(j+1,:); end end for i = 1:n-1 for j = 1:i P2(j,:) = (1-u)*P1(j,:) + u*P1(j+1,:); end end end
七、工程应用建议
- 工业设计:用于汽车/飞机外形曲面建模
- 计算机图形学:字体轮廓生成、游戏角色建模
- 机器人路径规划:生成平滑运动轨迹
- 有限元分析:构造复杂几何模型


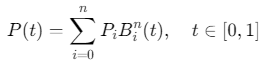
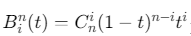 为Bernstein基函数,
为Bernstein基函数,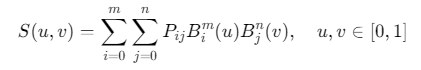

 浙公网安备 33010602011771号
浙公网安备 33010602011771号