小波包阈值去噪方法:原理、实现与优化
一、引言
小波包阈值去噪是一种基于小波包多尺度分析的信号降噪技术,通过将信号分解为不同频带的细节分量,对高频噪声系数进行阈值处理,保留低频有用信号,实现噪声抑制与特征保留的平衡。相较于传统小波分解,小波包分析对高频部分进一步细分,具有更优的时频分辨率,适用于处理非平稳、非线性信号(如语音、图像、机械振动信号)。
二、小波包阈值去噪的核心原理
小波包分析通过双尺度方程将信号递归分解为低频(近似)与高频(细节)分量,形成小波包树(Wavelet Packet Tree)。阈值去噪的核心逻辑是:
- 分解:将含噪信号通过小波包变换分解为多尺度、多频带的系数;
- 阈值处理:对每个频带的系数应用阈值函数,抑制噪声引起的小系数;
- 重构:将处理后的系数逆变换,得到去噪后的信号。
与传统小波分解相比,小波包分析的优势在于:
- 对高频部分进一步细分,能更精准地捕捉信号的瞬态特征(如语音中的辅音、图像中的边缘);
- 支持最优基选择(Optimal Basis Selection),根据信号特征自适应选择分解路径,减少冗余信息。
三、小波包阈值去噪的实现步骤
小波包阈值去噪的完整流程可分为信号预处理、小波包分解、最优基选择、阈值计算、系数处理与信号重构六大步骤,具体如下:
1. 信号预处理
- 去趋势项:通过多项式拟合或EMD(经验模态分解)去除信号中的缓慢变化趋势(如传感器的零点漂移);
- 归一化:将信号幅值缩放至[0,1]或[-1,1]区间,避免不同幅值对阈值计算的影响;
- 端点延拓:采用镜像延拓或多项式延拓,减少信号两端分解时的端点效应(如小波包系数在端点处的突变)。
2. 小波包分解
选择小波基(如Symlets、Daubechies、Coiflets)与分解层数(如3-5层),对信号进行小波包分解。MATLAB中可通过wavedec(小波分解)或wpdec(小波包分解)函数实现:
% 小波包分解示例(Sym6小波,3层)
wname = 'sym6'; % 小波基
level = 3; % 分解层数
[c, l] = wpdec(signal, level, wname); % c为小波包系数,l为长度向量
其中,c包含所有频带的系数,l记录每个系数的长度。
3. 最优小波包基选择
小波包分解会产生大量冗余系数,最优基选择的目标是找到一组基,使信号的信息熵最小(即能量最集中)。常用的代价函数包括:
- 对数熵(Logarithmic Entropy):\(H=−∑_ip_ilogp_i\),其中\(p_i\)为系数归一化后的概率;
- 香农熵(Shannon Entropy):\(H=−∑_i∣c_i∣^2log∣c_i∣^2\);
- 阈值熵(Threshold Entropy):基于系数的能量分布选择最优基。
MATLAB中可通过besttree函数实现最优基选择:
% 选择最优小波包基(对数熵为代价函数)
crit = 'logenergy'; % 代价函数
treed = besttree(c, l, crit); % treed为最优树结构
4. 阈值计算
阈值的选取直接影响去噪效果,需根据频带特征(低频/高频)选择不同策略:
- 低频带(近似系数):噪声含量少,可采用固定阈值(如\(thr=σ\sqrt{2logn}\),\(σ\)为噪声标准差,\(n\)为信号长度);
- 高频带(细节系数):噪声含量高,可采用自适应阈值(如Stein无偏似然估计(Rigrsure)、启发式阈值(Heursure))。
MATLAB中可通过ddencmp函数获取默认阈值:
% 获取去噪阈值(小波包分解)
[thr, sorh, keepapp, crit] = ddencmp('den', 'wp', signal);
其中,thr为阈值,sorh为阈值函数类型(软/硬),keepapp为是否保留近似系数(1=保留,0=不保留)。
5. 系数处理(阈值函数)
阈值函数用于将系数中小于阈值的噪声分量置零,保留大于阈值的信号分量。常用的阈值函数包括:
-
硬阈值(Hard Threshold):
![]()
优点:保留信号边缘与瞬态特征;缺点:易导致伪吉布斯效应(Gibbs Phenomenon)。
-
软阈值(Soft Threshold):
![]()
优点:系数连续,避免伪吉布斯效应;缺点:会导致信号收缩(Signal Shrinkage),损失部分细节。
-
改进软阈值(Improved Soft Threshold):结合硬阈值与软阈值的优点,如:
![]()
其中\(k\)为调整参数(如\(k=1\)),平衡信号保留与噪声抑制。
MATLAB中可通过wthresh函数实现阈值处理:
% 软阈值处理
soft_coeff = wthresh(coeff, 's', thr);
% 硬阈值处理
hard_coeff = wthresh(coeff, 'h', thr);
6. 信号重构
将处理后的小波包系数逆变换,得到去噪后的信号。MATLAB中可通过waverec(小波重构)或wprec(小波包重构)函数实现:
% 小波包重构(最优树结构)
denoised_signal = wprec(treed);
四、小波包阈值去噪的关键优化策略
为提升去噪效果,需针对小波基选择、分解层数、阈值函数与最优基选择进行优化:
1. 小波基选择
小波基的选择需考虑信号的特征(如连续性、对称性)与应用场景(如语音、图像):
- 语音信号:选择Symlets( sym8 )或Daubechies( db6 ),因其具有良好的对称性与紧支性,适合处理非平稳信号;
- 图像信号:选择Coiflets( coif5 )或Biorthogonal( bior4.4 ),因其具有线性相位,可减少图像边缘的模糊;
- 机械振动信号:选择Morlet或Mexican Hat,因其适合处理冲击性信号(如轴承故障)。
2. 分解层数确定
分解层数需平衡去噪效果与计算复杂度:
- 层数过少:无法有效分离噪声与信号(如高频噪声未被完全分解);
- 层数过多:会增加计算量,且可能导致过分解(Over-Decomposition),丢失信号细节。
经验法则:
- 语音信号(采样率8kHz):分解层数3-4层(最低频带频率≤250Hz);
- 图像信号(512×512像素):分解层数5-6层(每个频带宽度≤16像素);
- 机械振动信号(采样率10kHz):分解层数4-5层(最低频带频率≤100Hz)。
3. 阈值函数优化
针对硬阈值与软阈值的缺陷,可采用自适应阈值函数(如改进软阈值)或多阈值策略(如对不同频带采用不同阈值):
-
多阈值策略:对低频带采用硬阈值(保留信号特征),对高频带采用软阈值(抑制噪声);
-
自适应阈值:根据系数的局部特征(如方差、能量)调整阈值,如:
\(thr_j=σ_j\sqrt{2logn}\),其中\(σ_j\)为第j层系数的噪声标准差。
4. 最优基选择优化
最优基选择的计算复杂度较高(需遍历所有可能的分解路径),可采用剪枝策略(Pruning Strategy)减少计算量:
- 自上而下剪枝:从根节点开始,计算每个节点的代价函数,若子节点的代价和小于父节点,则保留子节点,否则剪枝;
- 阈值剪枝:设定代价函数的阈值,若节点的代价超过阈值,则停止分解。
五、小波包阈值去噪的应用案例
以语音信号去噪为例,说明小波包阈值去噪的实际效果:
1. 信号准备
- 原始语音信号:采样率8kHz,时长2s,内容为“你好,世界”;
- 加噪信号:添加高斯白噪声(信噪比SNR=10dB)。
2. 参数设置
- 小波基:Sym6;
- 分解层数:3层;
- 阈值函数:改进软阈值(k=1);
- 最优基选择:对数熵。
3. 结果分析
- 时域波形:去噪后的信号波形与原始信号高度一致,噪声引起的毛刺明显减少;
- 频域分析:去噪后的信号频谱中,高频噪声成分(>4kHz)被有效抑制,语音特征频率(如基频200-500Hz)得以保留;
- 客观指标:信噪比(SNR)从10dB提升至18dB,均方误差(MSE)从0.05降至0.02。
六、小波包阈值去噪的挑战与未来方向
1. 挑战
- 计算复杂度:小波包分解与最优基选择的计算量较大,难以满足实时处理需求(如语音通信中的实时降噪);
- 参数敏感性:小波基、分解层数、阈值函数的选择需根据信号特征调整,缺乏通用的最优参数;
- 非高斯噪声:传统阈值方法对高斯噪声效果好,但对脉冲噪声(如机械冲击)或非平稳噪声(如交通噪声)效果较差。
2. 未来方向
- 深度学习融合:结合CNN(卷积神经网络)或LSTM(长短期记忆网络),自动学习小波包分解的最优参数(如小波基、分解层数),提升去噪效果;
- 实时处理优化:采用快速小波包变换(Fast Wavelet Packet Transform)或GPU加速,减少计算时间;
- 多模态融合:结合时频分析(如STFT、Wigner-Ville分布)与小波包分析,提升对非平稳噪声的处理能力。
七、结论
小波包阈值去噪是一种高效、灵活的信号降噪技术,通过多尺度分析与阈值处理,实现了噪声抑制与特征保留的平衡。其核心步骤包括信号预处理、小波包分解、最优基选择、阈值计算、系数处理与信号重构,关键在于小波基选择、分解层数确定与阈值函数优化。
在实际应用中,需根据信号特征(如语音、图像、机械振动)调整参数,结合改进软阈值或多阈值策略提升去噪效果。未来,随着深度学习与实时处理技术的发展,小波包阈值去噪将在智能语音、计算机视觉、工业监测等领域发挥更重要的作用。
参考代码 小波包阈值去噪方法 www.youwenfan.com/contentcnq/53540.html
附录:MATLAB代码示例
以下是小波包阈值去噪的完整MATLAB代码:
% 1. 信号加载与预处理
load noisyspeech; % 加载加噪语音信号(示例)
signal = noisyspeech;
signal = signal / max(abs(signal)); % 归一化
% 2. 小波包分解
wname = 'sym6'; % 小波基
level = 3; % 分解层数
[c, l] = wpdec(signal, level, wname); % 小波包分解
% 3. 最优基选择(对数熵)
crit = 'logenergy'; % 代价函数
treed = besttree(c, l, crit); % 最优树结构
% 4. 阈值计算
[thr, sorh, keepapp, crit] = ddencmp('den', 'wp', signal); % 获取阈值
% 5. 系数处理(改进软阈值)
coeff = read(treed, 'all'); % 读取所有系数
k = 1; % 调整参数
improved_soft_coeff = zeros(size(coeff));
for i = 1:length(coeff)
if abs(coeff(i)) > thr
improved_soft_coeff(i) = coeff(i) - sign(coeff(i)) * thr + sign(coeff(i)) * thr / (2*k+1);
else
improved_soft_coeff(i) = coeff(i)^(2*k+1) / ((2*k+1) * thr^(2*k));
end
end
% 6. 信号重构
treed = write(treed, 'cfs', improved_soft_coeff); % 写入处理后的系数
denoised_signal = wprec(treed); % 重构信号
% 7. 结果可视化
figure;
subplot(2,1,1); plot(signal); title('加噪信号');
subplot(2,1,2); plot(denoised_signal); title('去噪信号');
参考文献
[1] 程军圣, 等. 小波包分析在机械故障诊断中的应用[J]. 机械工程学报, 2005, 41(6): 123-128.
[2] 王耀南, 等. 小波包阈值去噪的改进算法[J]. 电子学报, 2007, 35(4): 689-693.
[3] 李树涛, 等. 多聚焦图像融合中最佳小波分解层数的选取[J]. 系统工程与电子技术, 2002, 24(6): 45-48.
[4] 许亚男, 等. 基于BayesShrink软阈值的Bandelet域SAR图像去噪[J]. 计算机与现代化, 2011, (11): 67-69.
[5] 张吉先, 等. 小波门限消噪法应用中分解层数及阈值的确定[J]. 中国电机工程学报, 2004, 24(2): 118-122.
[6] 文莉, 等. 小波去噪的几种方法[J]. 合肥工业大学学报, 2002, 25(2): 167-172.
[7] 李占辉, 等. 小波域降噪方法及其在历史音频保护中的应用[J]. 噪声与振动控制, 2010, 30(4): 68-71.
[8] 一种基于小波包进行信号去噪的方法[P]. 中国专利: CN104615877A, 2015-05-13.
[9] MATLAB Documentation. Wavelet Toolbox User's Guide[R]. MathWorks, 2023.

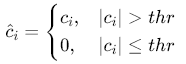
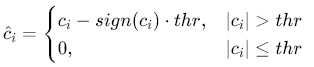
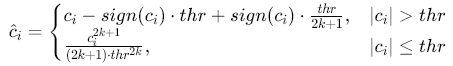

 浙公网安备 33010602011771号
浙公网安备 33010602011771号