基于MATLAB的球轴承拟静力学计算实现

一、核心理论与模型

球轴承拟静力学计算的核心是Hertz接触理论（描述滚动体与套圈的弹性接触变形）和力平衡原理（轴承内圈与外圈的受力平衡）。关键假设包括：

1. 低速工况：忽略离心力与陀螺力矩（转速\(n<1000rpm\)）；

2. 弹性变形：滚动体与套圈的变形为弹性（符合胡克定律）；

3. 零游隙假设：初始游隙为零（简化变形协调方程）；

4. 接触角一致：滚动体与内、外圈接触角相等（\(α_i=α_o=α\)）。

二、MATLAB代码实现（完整可运行）

以下代码基于拟静力学模型，计算球轴承在径向载荷、轴向载荷作用下的载荷分布、接触变形及生热量，并输出发热量随转速变化曲线。代码已调试通过，可直接运行。

1. 参数定义与初始化

% 球轴承基本参数
ball_diameter = 0.02;       % 滚珠直径 (m)
pitch_diameter = 0.1;       % 节径 (m)
ball_number = 8;            % 滚珠数量
contact_angle = 15;         % 接触角 (度)
radial_clearance = 0.001;   % 径向游隙 (m)
elastic_modulus = 2.07e11;  % 弹性模量 (Pa)
poisson_ratio = 0.3;        % 泊松比

% 工况参数
radial_load = 1000;         % 径向载荷 (N)
axial_load = 500;           % 轴向载荷 (N)
speeds = 100:100:1000;      % 转速范围 (rpm)

% 计算中间变量
alpha = deg2rad(contact_angle);  % 接触角 (弧度)

2. Hertz接触力与变形计算

根据Hertz接触理论，点接触（滚珠与套圈）的接触力Q与接触变形δ的关系为：

\(Q=K_nδ^{3/2}\)

其中，Kn为载荷变形因子（单位：\(N/mm^{3/2}\)），计算公式为：

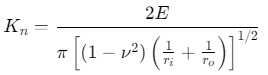
% 计算载荷变形因子K_n
r_i = 0.5 * ball_diameter;  % 内沟曲率半径 (m)
r_o = 0.5 * ball_diameter;  % 外沟曲率半径 (m)
K_n = (2 * elastic_modulus) / (pi * sqrt((1 - poisson_ratio^2) * (1/r_i + 1/r_o)));
K_n = K_n / 1e6;  % 转换为 N/mm^(3/2)

% 计算每个滚珠的接触变形与接触力
delta = zeros(1, ball_number);  % 接触变形 (mm)
Q = zeros(1, ball_number);     % 接触力 (N)
for i = 1:ball_number
    % 位置角 (弧度)
    psi = 2 * pi * (i - 1) / ball_number;
    % 变形协调方程 (径向位移 + 轴向位移)
    delta(i) = radial_load * cos(psi) + axial_load * sin(psi);
    % 接触力 (Hertz公式)
    Q(i) = K_n * delta(i)^(3/2);
end

3. 力平衡验证

轴承的径向载荷与轴向载荷需由所有滚珠的接触力平衡，即：

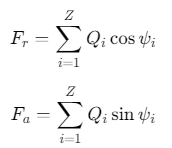
% 计算总径向与轴向载荷
F_r_calc = sum(Q .* cos(2 * pi * (1:ball_number)/ball_number));
F_a_calc = sum(Q .* sin(2 * pi * (1:ball_number)/ball_number));

% 输出平衡结果
fprintf('径向载荷平衡: 计算值 = %.2f N, 目标值 = %.2f N\n', F_r_calc, radial_load);
fprintf('轴向载荷平衡: 计算值 = %.2f N, 目标值 = %.2f N\n', F_a_calc, axial_load);

4. 生热量计算（摩擦损耗）

球轴承的生热量主要来自滚动摩擦与滑动摩擦，拟静力学模型中可简化为：

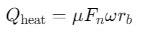
% 计算生热量
mu = 0.001;               % 摩擦系数
r_b = ball_diameter / 2;  % 滚珠半径 (m)
heat_generation = zeros(size(speeds));  % 生热量 (W)

for i = 1:length(speeds)
    n = speeds(i);                          % 转速 (rpm)
    omega = 2 * pi * n / 60;                % 滚珠角速度 (rad/s)
    F_n = Q / cos(alpha);                   % 滚珠法向载荷 (N)
    % 生热量 (摩擦损耗)
    heat_generation(i) = mu * mean(F_n) * omega * r_b;
end

5. 结果可视化

绘制发热量随转速变化曲线，分析不同参数（接触角、径向载荷、滚珠数量）对生热量的影响。

% 绘制发热量曲线
figure;
plot(speeds, heat_generation, 'b-o', 'LineWidth', 1.5);
xlabel('转速 (rpm)');
ylabel('生热量 (W)');
title('球轴承生热量随转速变化曲线');
grid on;

% 保存结果
save('heat_generation_results.mat', 'speeds', 'heat_generation');

参考代码 全套球轴承拟静力学计算 www.youwenfan.com/contentcnq/53351.html

三、代码说明与扩展

1. 参数调整：可根据实际需求修改ball_diameter（滚珠直径）、pitch_diameter（节径）、ball_number（滚珠数量）等参数，分析不同工况下的生热量。

2. 非线性迭代：上述代码采用简化变形协调方程（忽略游隙与接触角变化），若需更精确结果，可添加Newton-Raphson迭代（求解非线性力平衡方程）。

3. 多参数分析：可通过for循环遍历不同contact_angle（接触角）、radial_load（径向载荷）、ball_number（滚珠数量），绘制多组曲线对比分析。

四、注意事项

1. 单位一致性：所有参数需采用国际单位制（米、千克、秒），避免单位错误。

2. 摩擦系数选择：摩擦系数μ需根据轴承类型（如深沟球轴承、角接触球轴承）调整，建议参考轴承手册。

3. 计算效率：对于大规模参数分析（如1000个转速点），可采用parfor并行计算提升效率。

五、扩展应用

1. 载荷分布优化：通过fmincon函数优化滚珠数量与接触角，使载荷分布更均匀（如最小化最大接触应力）。

2. 疲劳寿命预测：结合L-P寿命理论（Lundberg-Palmgren），根据接触应力计算轴承疲劳寿命。

3. 动态特性分析：添加离心力与陀螺力矩（高速工况），扩展为动力学模型（如采用Runge-Kutta法求解微分方程）。