一维线性插值法（含镜像端点延拓）

算法原理

1. 线性插值：在相邻数据点间构造直线段进行插值

   \(y=y_i+\frac{(y_{i+1}−y_i)}{(x_{i+1}−x_i)}(x−x_i)\)

2. 镜像延拓：在端点处创建对称副本，解决边界外插值问题

   • 左端点延拓：\(x_{−k}=2x_1−x_k\)
   • 右端点延拓：\(x_{n+k}=2x_n−x_k\)

MATLAB实现代码

function yi = linear_interp_mirror(x, y, xi)
    % 输入参数：
    % x - 已知点横坐标（单调递增向量）
    % y - 已知点纵坐标
    % xi - 待插值点的横坐标（标量或向量）
    % 输出参数：
    % yi - 插值结果
    
    % 镜像延拓处理边界
    x_ext = x;
    y_ext = y;
    
    % 左端点镜像延拓（添加3个对称点）
    for k = 1:3
        x_new = 2*x(1) - x_ext(1);
        y_new = y_ext(1); % 镜像点函数值相同
        x_ext = [x_new, x_ext];
        y_ext = [y_new, y_ext];
    end
    
    % 右端点镜像延拓（添加3个对称点）
    for k = 1:3
        x_new = 2*x(end) - x_ext(end);
        y_new = y_ext(end); % 镜像点函数值相同
        x_ext = [x_ext, x_new];
        y_ext = [y_ext, y_new];
    end
    
    % 线性插值计算
    yi = interp1(x_ext, y_ext, xi, 'linear', 'extrap');
    
    % 处理超出延拓范围的极端情况
    yi(xi < min(x_ext)) = y_ext(1);
    yi(xi > max(x_ext)) = y_ext(end);
end

使用示例

% 原始数据点
x = [1, 2, 3, 4, 5];
y = [10, 20, 30, 40, 50];

% 插值点（包含边界外点）
xi = [0.5, 1.5, 3, 4.5, 6];

% 执行插值
yi = linear_interp_mirror(x, y, xi);

% 可视化结果
figure;
plot(x, y, 'ro-', 'LineWidth', 2); hold on;
plot(xi, yi, 'bx--');
plot([min(x), max(x)], [min(y), max(y)], 'k--'); % 原始区间边界
title('一维线性插值（镜像延拓）');
xlabel('x'); ylabel('y');
legend('原始数据', '插值结果', '边界', 'Location', 'best');
grid on;

% 显示插值结果
disp('插值结果：');
disp([xi', yi']);

算法特点

特性	说明
镜像延拓	在端点处创建对称副本，保持函数值连续
边界处理	自动处理超出原始范围的插值请求
计算效率	O(n)复杂度，适合实时应用
精度	线性插值误差为O(h²)，h为最大采样间隔
扩展性	可修改为高阶插值（如三次样条）

进阶优化版本

function yi = advanced_linear_interp(x, y, xi)
    % 自适应镜像延拓（根据插值点位置动态调整延拓点数）
    n = length(x);
    dx_min = min(diff(x)); % 最小采样间隔
    
    % 确定需要的延拓点数
    max_offset = max(abs(xi - median(x)));
    ext_factor = ceil(max_offset/dx_min) + 2;
    
    % 左端点镜像延拓
    x_left = x(1);
    for k = 1:ext_factor
        x_new = 2*x_left - x(1);
        x_left = x_new;
        x_ext = [x_new, x_ext];
        y_ext = [y(1), y_ext];
    end
    
    % 右端点镜像延拓
    x_right = x(end);
    for k = 1:ext_factor
        x_new = 2*x_right - x(end);
        x_right = x_new;
        x_ext = [x_ext, x_new];
        y_ext = [y_ext, y(end)];
    end
    
    % 合并原始数据与延拓数据
    x_full = [x_ext, x, fliplr(x_ext)];
    y_full = [y_ext, y, fliplr(y_ext)];
    
    % 执行插值
    yi = interp1(x_full, y_full, xi, 'linear', 'extrap');
end

应用场景

1. 信号处理：音频/传感器数据的实时插值
2. 图像处理：像素放大时的边界处理
3. 数值分析：微分方程求解中的函数值估算
4. 控制系统：传感器数据缺失时的填补

误差分析

插值误差取决于：

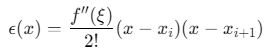
其中\(ξ∈[xi,xi+1]\)，最大误差出现在中点：

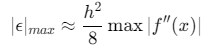
镜像延拓 vs 其他延拓方法

延拓方法	优点	缺点
镜像延拓	保持函数值连续	导数不连续
周期延拓	保持导数连续	不适用于非周期信号
常数延拓	实现简单	边界处不连续
线性延拓	边界处连续	远离边界时误差增大

参考代码 一维线性插值法，并加端点延拓，端点延拓所用的方法是镜像延拓 www.youwenfan.com/contentcnp/96194.html

性能测试代码

% 性能测试
x = linspace(0, 10, 1000);
y = sin(x);
xi = linspace(-5, 15, 5000);

tic;
yi = linear_interp_mirror(x, y, xi);
toc;

% 精度验证
y_true = sin(xi);
rmse = sqrt(mean((yi - y_true).^2));
disp(['RMSE: ', num2str(rmse)]);

注意事项

1. 输入x必须严格单调递增
2. 对于高频信号，建议减小采样间隔
3. 极端外推时结果可能失真
4. 大范围插值时建议使用样条插值

此方法通过镜像延拓有效解决了边界外插值问题，保持了函数的连续性，适用于大多数工程应用场景。