基于MATLAB的混沌优化算法求极值实现

混沌优化算法（Chaos Optimization Algorithm, COA）通过混沌运动的遍历性和随机性实现全局搜索，结合MATLAB的矩阵运算优势，可高效求解复杂函数极值。

---

一、核心算法流程

---

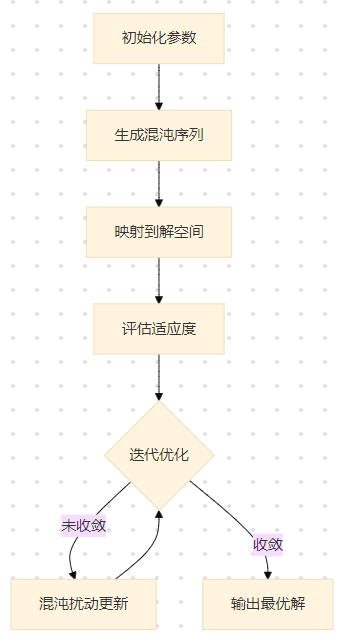
二、MATLAB代码实现（以Rastrigin函数为例）

%% 参数设置
clear; clc;
nPop = 30;        % 种群规模
maxIter = 100;    % 最大迭代次数
dim = 2;          % 问题维度
lb = -5.12;       % 下界
ub = 5.12;        % 上界

%% 混沌初始化（Logistic映射）
mu = 4;           % Logistic参数
chaosSeq = zeros(nPop,dim);
for i = 1:nPop
    x = rand(1,dim);
    for j = 1:100
        x = mu * x .* (1 - x);  % 生成混沌序列
    end
    chaosSeq(i,:) = x;
end

%% 解空间映射
pop = lb + (ub - lb) .* chaosSeq;

%% 适应度计算（Rastrigin函数）
fitness = zeros(nPop,1);
for i = 1:nPop
    x = pop(i,:);
    A = 10;
    fitness(i) = A * dim + sum(x.^2 - A*cos(2*pi*x));
end

%% 迭代优化
bestIdx = 1;
bestFit = fitness(1);
trace = zeros(maxIter,1);
trace(1) = bestFit;

for iter = 2:maxIter
    % 混沌扰动更新
    for i = 1:nPop
        % 选择三个不同个体
        r1 = randi([1,nPop]); r2 = randi([1,nPop]); r3 = randi([1,nPop]);
        while r1 == r2 || r1 == r3 || r2 == r3
            r1 = randi([1,nPop]); r2 = randi([1,nPop]); r3 = randi([1,nPop]);
        end
        
        % 位置更新（改进Logistic映射）
        pop(i,:) = pop(i,:) + 0.5*(pop(r1,:) - pop(r2,:)) + ...
                  0.3*(bestPop - pop(r3,:));
        
        % 边界处理
        pop(i,:) = max(pop(i,:), lb);
        pop(i,:) = min(pop(i,:), ub);
    end
    
    % 适应度更新
    for i = 1:nPop
        x = pop(i,:);
        A = 10;
        fitness(i) = A * dim + sum(x.^2 - A*cos(2*pi*x));
    end
    
    % 更新最优解
    [currentBest, idx] = min(fitness);
    if currentBest < bestFit
        bestFit = currentBest;
        bestIdx = idx;
    end
    
    % 记录收敛曲线
    trace(iter) = bestFit;
    
    % 动态调整参数（自适应策略）
    mu = 4 - 3.9*exp(-0.1*iter);  % Logistic参数衰减
end

%% 结果可视化
figure;
plot(trace,'LineWidth',2);
xlabel('迭代次数'); ylabel('最优适应度');
title('混沌优化收敛曲线');

% 最优解位置
bestPos = pop(bestIdx,:);
disp(['最优解: ', num2str(bestPos')]);
disp(['最优值: ', num2str(bestFit)]);

---

三、改进

1. 混沌映射优化

   • Tent映射替代Logistic：解决Logistic在边界区域的聚集问题

     function x = tent_map(x)
         if x < 0.5
             x = 2*x;
         else
             x = 2*(1-x);
         end
     end
     

2. 混合搜索策略

   • 精英保留机制：保留历史最优解参与下一代迭代

   • 自适应步长：根据迭代次数动态调整搜索步长

     step = 0.5 * (1 - iter/maxIter);  % 线性衰减
     

3. 多混沌系统耦合

   • 同时使用Logistic和Lorenz系统生成扰动序列

     % Lorenz混沌序列生成
     sigma = 10; rho = 28; beta = 8/3;
     x = 1; y = 1; z = 1;
     for i = 1:1000
         dx = sigma*(y - x);
         dy = x*(rho - z) - y;
         dz = x*y - beta*z;
         x = x + dx*0.01;
         y = y + dy*0.01;
         z = z + dz*0.01;
         lorenzSeq(i) = x;
     end
     

---

四、应用场景示例

1. PID参数优化

   % 目标函数：PID控制器的ITAE指标
   function itae = pid_obj(Kp,Ki,Kd)
       % 系统模型参数
       a = 0.1; b = 0.2;
       num = [Kd Kp];
       den = [1 2*a Kp b];
       sys = tf(num,den);
   
       % 时域积分指标计算
       [y,t] = step(sys);
       itae = trapz(t, t.*abs(y));
   end
   

2. 神经网络权值优化

   % 定义网络结构
   net = feedforwardnet([10 5]);
   net.trainFcn = 'trainlm';
   
   % 混沌优化权值
   w = getwb(net);
   chaosW = lb + (ub - lb) .* chaosSeq;
   net = setwb(net, chaosW');
   

---

五、注意事项

1. 参数敏感性 混沌参数（如Logistic的μ值）需根据问题特性调整，建议范围3.57~4

2. 计算效率

   • 对高维问题（>10维）建议采用并行计算：

     parfor i = 1:nPop
         % 并行计算适应度
     end
     

3. 混合算法

   • 与模拟退火结合：

     if rand < exp(-(newFit - oldFit)/T)
         accept = true;
     end
     

参考代码 一种混沌优化算法求极值的方法 www.youwenfan.com/contentcnn/83909.html

六、扩展应用

1. 多目标优化

   • 引入Pareto前沿筛选机制

     % 非支配排序
     [fronts, ranks] = nonDominatedSort(fitness);
     

2. 动态环境适应

   • 在线更新混沌参数：

     mu = 4 - 0.1*iter;  % 随迭代次数衰减