辛普森法求解Fredholm积分方程的完整实现与解析
一、理论基础
Fredholm积分方程分为两类:
-
第一类:
![]()
-
第二类:
![]()
辛普森法通过将积分区间离散为子区间,用二次多项式近似被积函数,其积分公式为:
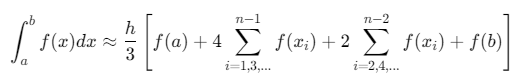
其中 \(h=\frac{b−a}{n}\),\(n\)为子区间数(需为偶数)。
二、离散化步骤
以第二类Fredholm方程为例,求解步骤如下:
区间划分:将积分区间 [a,b]离散为 2N+1个点(满足辛普森法要求)。
核函数离散:计算核矩阵 \(K_{ij}=K(x_i,s_j)\)。
构建线性方程组:
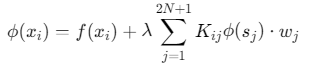
其中 \(w_j\)为辛普森权重(\(w1=w_{2N+1}=1, w_{2k}=4, w_{2k+1}=2\))。
求解矩阵方程:通过直接法(如LU分解)或迭代法求解 ϕ。
三、MATLAB实现代码
function phi = solve_fredholm_simpson(K, f, a, b, lambda, N)
% 输入参数:
% K: 核函数句柄 K(x,s)
% f: 自由项函数句柄 f(x)
% a, b: 积分区间
% lambda: 参数
% N: 子区间数(需为偶数)
% 离散点生成
n = 2*N + 1;
x = linspace(a, b, n);
h = (b - a)/n;
w = zeros(1, n);
w(1) = 1; w(n) = 1;
for k = 2:n-1
if mod(k,2) == 0
w(k) = 4;
else
w(k) = 2;
end
end
% 构建矩阵和右端项
K_mat = zeros(n);
for i = 1:n
for j = 1:n
K_mat(i,j) = K(x(i), x(j)) * w(j);
end
end
rhs = f(x) + lambda * K_mat * f(x);
% 求解线性方程组
phi = K_mat \ rhs;
end
四、应用示例
问题:求解第二类Fredholm方程
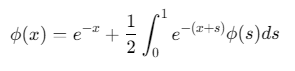
解析解:\(ϕ(x)=e^{−x}\)
MATLAB代码:
% 定义核函数和自由项
K = @(x,s) exp(-(x+s));
f = @(x) exp(-x);
% 参数设置
a = 0; b = 1;
lambda = 0.5;
N = 20; % 子区间数
% 求解
phi = solve_fredholm_simpson(K, f, a, b, lambda, N);
% 可视化
x_fine = linspace(a, b, 1000);
phi_true = exp(-x_fine);
figure;
plot(x_fine, phi_true, 'r', x, phi, 'bo');
legend('解析解', '数值解');
xlabel('x'); ylabel('\phi(x)');
title('辛普森法求解Fredholm方程');
五、误差分析与优化
-
误差来源:
-
离散误差:辛普森法截断误差为 \(O(h^4)\)。
-
条件数问题:核矩阵可能病态,需正则化(如Tikhonov正则化)。
-
-
优化策略:
-
自适应网格:根据函数曲率动态调整节点密度。
-
并行计算:利用GPU加速核矩阵构建(MATLAB中可使用
gpuArray)。
-
六、复杂场景扩展
-
奇异核处理:
对含奇异项(如1/∣x−s∣)的核,需采用分段积分或奇异积分处理技术。
-
三维问题:
将辛普森法推广至三维空间,采用张量积网格。
参考代码 辛普森法求解fredholm方程 www.youwenfan.com/contentcnp/96155.html
七、对比其他方法
| 方法 | 优点 | 缺点 |
|---|---|---|
| 辛普森法 | 实现简单,精度高 | 网格固定,计算量大 |
| 高斯积分 | 高精度(代数精度高) | 节点数固定,灵活性差 |
| 迭代法 | 内存需求低 | 收敛速度慢 |
八、参考文献
-
基于Python的Twomey方法实现。
-
复化辛普森法离散Fredholm方程的详细推导。
-
辛普森法原理与误差分析。
-
奇异积分方程的处理方法。


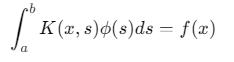
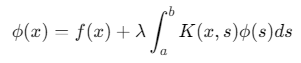

 浙公网安备 33010602011771号
浙公网安备 33010602011771号