三维凸包学习小记

三维凸包

Tags：高级算法

---

Part 1 平面几何基础

出门右拐：https://www.cnblogs.com/xzyxzy/p/10033130.html （附计算几何题单）

Part 2 立体几何基础

向量运算

加减运算

同平面向量，对应坐标相加减

模长

\(|a|=\sqrt{x^2+y^2+z^2}\)

点积

两个向量的点积仍然表示 a到b的投影×b的模长
仍然满足\(a·b=|a||b|cos<a,b>\)
坐标下有\((x_1,y_1,z_1)·(x_2,y_2,z_2)=x_1x_2+y_1y_2+z_1z_2\)，对应坐标相乘

叉积

两个三维向量叉积仍然是一个三维向量（不同于平面向量，乘积是实数）
其模长仍然表示以这两个三维向量作为邻边的平行四边形面积
方向符合：对于\(a*b\)，伸出右手，食指指向\(a\)，中指指向\(b\)，大拇指所对的方向为叉积后的向量方向

如上图，\(AC*AB=AD\)

坐标表示就是：\((y_1z_2-z_1y_2，z_1x_2-x_1z_2，x_1y_2-y_1x_2)\)

平面的法向量

在平面上任选两个向量做叉积即可

判断点是否在平面上

平面ABC，判断D是否在平面上。
法向量n，则若AD&n=0，点积为零，说明D在平面上。

点到平面的距离

该点到平面上任意一点的向量 点积 平面的法向量
然后除以法向量的模长

double Dis(Node a) {Node w=Normal();return fabs((w&(a-A[v[0]]))/w.len());}

求凸包

扰动

首先对其微小扰动，避免出现四点共面的情况

平面的记录

扰动之后各个平面一定是一个三角形，逆时针方向记录三个顶点表示一个面

增量构造

借用网上这篇博客的图片方便理解
对于一个已知凸包，新增一个点P
将P视作一个点光源，向凸包做射线
可以知道，光线的可见面和不可见面一定是由若干条棱隔开的

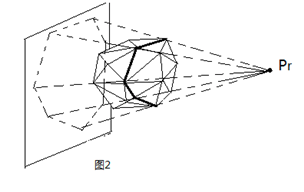
将光的可见面删去，并新增由其分割棱与P构成的平面

重复此过程即可，复杂度\(O(n^2)\)，分析见Pick定理、欧拉公式和圆的反演。

代码

洛谷模板：求三维凸包面积
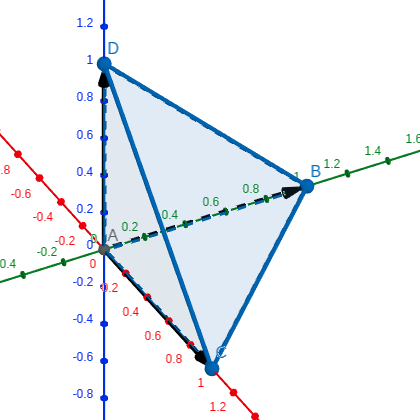
先放上样例的两张靓照：

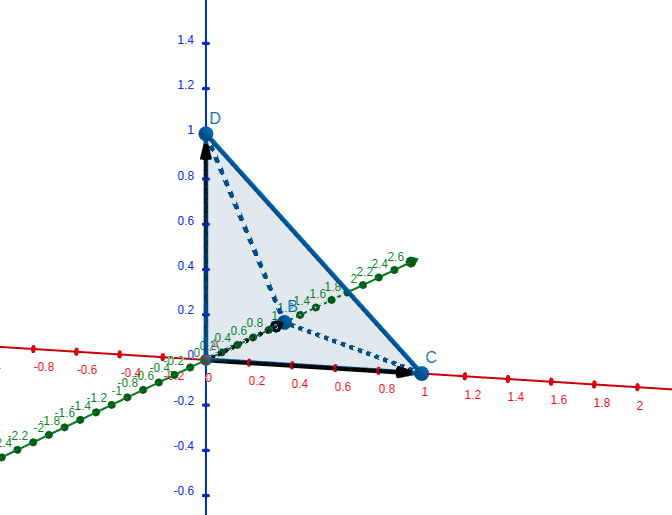
强烈推荐画图软件Geogebra！

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cmath>
using namespace std;
const int N=2010;
const double eps=1e-9;
int n,cnt,vis[N][N];
double ans;
double Rand() {return rand()/(double)RAND_MAX;}
double reps() {return (Rand()-0.5)*eps;}
struct Node
{
	double x,y,z;
	void shake() {x+=reps();y+=reps();z+=reps();}
	double len() {return sqrt(x*x+y*y+z*z);}
	Node operator - (Node A) {return (Node){x-A.x,y-A.y,z-A.z};}
	Node operator * (Node A) {return (Node){y*A.z-z*A.y,z*A.x-x*A.z,x*A.y-y*A.x};}
	double operator & (Node A) {return x*A.x+y*A.y+z*A.z;}
}A[N];
struct Face
{
	int v[3];
	Node Normal() {return (A[v[1]]-A[v[0]])*(A[v[2]]-A[v[0]]);}
	double area() {return Normal().len()/2.0;}
}f[N],C[N];
int see(Face a,Node b) {return ((b-A[a.v[0]])&a.Normal())>0;}
void Convex_3D()
{
	f[++cnt]=(Face){1,2,3};
	f[++cnt]=(Face){3,2,1};
	for(int i=4,cc=0;i<=n;i++)
	{
		for(int j=1,v;j<=cnt;j++)
		{
			if(!(v=see(f[j],A[i]))) C[++cc]=f[j];
			for(int k=0;k<3;k++) vis[f[j].v[k]][f[j].v[(k+1)%3]]=v;
		}
		for(int j=1;j<=cnt;j++)
			for(int k=0;k<3;k++)
			{
				int x=f[j].v[k],y=f[j].v[(k+1)%3];
				if(vis[x][y]&&!vis[y][x]) C[++cc]=(Face){x,y,i};
			}
		for(int j=1;j<=cc;j++) f[j]=C[j];
		cnt=cc;cc=0;
	}
}
int main()
{
	cin>>n;
	for(int i=1;i<=n;i++) cin>>A[i].x>>A[i].y>>A[i].z,A[i].shake();
	Convex_3D();
	for(int i=1;i<=cnt;i++) ans+=f[i].area();
	printf("%.3f\n",ans);
}