计算几何基础
计算几何基础
Tags:高级算法
前言
Noip爆炸后差点退组。
不取模设小上界的人大概不配学计算几何吧。
copy一些网上的博客好了。
计算几何详解:https://blog.csdn.net/clover_hxy/article/details/53966405
凸包详解:http://www.cnblogs.com/aiguona/p/7232243.html
旋转卡壳:https://blog.csdn.net/wang_heng199/article/details/74477738
题目标签:WFJ
声明一下:一下代码片段现已统一格式:*表示叉积,&表示点积,^表示数乘。符合博主现在的码风。当然对于实数并不存在运算符混淆问题。
向量线段相关
点积
\(a.x*b.x+a.y*b.y\)
叉积
\(a.x*b.y-a.y*b.x\)
借图:左边是点积,右边是叉积
转角公式
逆时针旋转角度\(B\)
原:\((cosAr,sinAr)\)
现:\((cos(A+B)r,sin(A+B)r)=((cosAcosB-sinAsinB)r,(sinAcosB+cosAsinB)r)\)
即:\((x,y)->(xcosB-ysinB,xsinB+ycosB)\)
极角排序
两种方法
\(atan2\)
这是一个给定三角形对边和邻边算角的函数,在cmath库中
对每个向量求\(angle=atan2(a.y,a.x)\)后直接排序即可
举例:\(atan2(1,1)=0.78,atan2(1,0)=1.57\)
叉积
叉积的正负可以判断左右关系,所以在最大跨角不超过180度的时候可以非常好地实现,否则有可能随机一个起点绕好几圈
两直线夹角
若两个向量都是从原点出发,则可以很方便地用$$\theta =atan2(x*y,x&y)$$叉积是平行四边形,底乘高;点积是底乘投影。
更特殊点,该夹角是有向夹角,从x向量旋转到y,逆时针是正角、顺时针是负角。
两直线交点
面积比->线段比->定比分点
Node Crosss(Node a1,Node a2,Node b1,Node b2)
{
Node a=a2-a1,b=b2-b1,c=b1-a1;
if(fabs(b*a)<1e-12) return (Node){-1e9,-1e9};//平行
double t=(b*c)/(b*a);
return a1+(a^t);
}
给个图形象一点(之前画错了orzFlashHu)
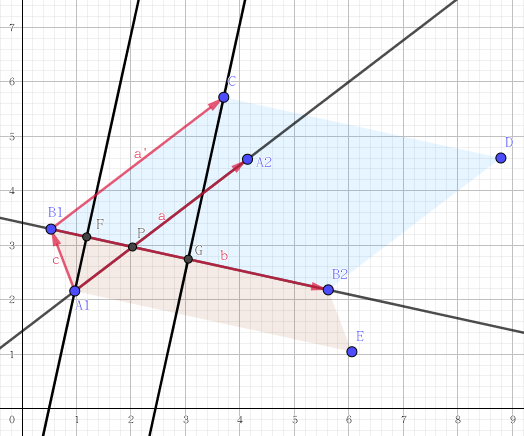
判断两线段是否相交
\(a1,a2,b1,b2\)为两条直线的两个端点
如果满足\((b1-a1)×(b1-a2)\)和\((b2-a1)×(b2-a2)\)不同号,并且\((a1-b1)×(a1-b2)\)和\((a2-b1)×(a2-b2)\)不同号,则两线段相交,叫跨立实验。
多边形相关
凸包
找到最下的点设为原点,将剩下的点用叉积极角排序
用单调栈维护凸包,当\((A[i]-A[sta[top-1]])×(A[sta[top]]-A[sta[top-1]])\)为非负时需要弹栈
int cmp1(const Node&A,const Node&B) {return A.y<B.y||(A.y==B.y&&A.x<B.x);}
int cmp2(const Node&A,const Node&B) {return A*B>0||(A*B==0&&A.dis()<B.dis());}
//这个表示如果两向量共线,把短的放前面(方便被踢开)
void Tubao()
{
sort(A+1,A+n+1,cmp1);//找到最底下的点
for(int i=n;i>=1;i--) A[i]=A[i]-A[1];
sort(A+2,A+n+1,cmp2);//极角排序
for(int i=1;i<=n;sta[++top]=i,i++)
while(top>=2&&(A[i]-A[sta[top-1]])*(A[sta[top]]-A[sta[top-1]])>=0) top--;
n=top;for(int i=1;i<=top;i++) A[i]=A[sta[i]];
}
判断点是否在多边形内
从该点向右引射线,与多边形交奇数次即在其内。
顺时针+1,逆时针-1,注意与顶点重合的情况
\(Practice:Codeforces375C\ Circling\ Round\ Treasures\)
判断点是否在凸包内
先判定和边界的关系
然后找到与其极角相邻的两点,凭此判断
须保证\(A[1]=(0,0)\)
ll in(Node a)
{
if(a*A[1]>0||A[tot]*a>0) return 0;
ll ps=lower_bound(A+1,A+tot+1,a,cmp2)-A-1;
return (a-A[ps])*(A[ps%tot+1]-A[ps])<=0;
}
求多边形面积
逆时针极角排序后直接用叉积求
double CalcS()
{
double res=0;
for(int i=2;i<node;i++) res+=(A[i]-A[1])*(A[i+1]-A[1]);
return res/2;
}
三角形重心
三点各坐标的平均值\((\frac{x1+x2+x3}{3},\frac{y1+y2+y3}{3})\)
算法
半平面交
用来求解一类线性规划问题?
首先存一个极大的凸多边形,考虑增加一条直线
那么将其视为一个向量,左边的为合法半平面
复杂度\(O(n^2)\)
void Cut(Node a,Node b)//增加一个向量
{
A[tt+1]=A[1];c=0;
for(int i=1;i<=tt;i++)//枚举每一条边
{
double v1=(A[i]-a)*(A[i]-b);
double v2=(A[i+1]-a)*(A[i+1]-b);
if(v1>=0) C[++c]=A[i];//如果A[i]在合法平面内则存入
if(v1*v2<0) Add(A[i],A[i+1],a,b);//如果边(A[i],A[i+1])穿过新增直线,把交点加入
}
tt=c;for(int i=1;i<=tt;i++) A[i]=C[i];
}
如果不是凸多边形的时候,可以采用水平可见直线的方法,先按照斜率排序后直接用栈维护下平面。复杂度为排序复杂度,有一定局限性,但在坐标范围较大采用上面方法会炸精度时非常好用
struct Line{int k,b;int id;}A[N];
int cmp1(const Line&A,const Line&B) {return A.k<B.k||(A.k==B.k&&A.b>B.b);}
double Node(int i,int j) {return 1.0*(A[j].b-A[i].b)/(A[i].k-A[j].k);}
void work()
{
sort(A+1,A+n+1,cmp1);
for(int i=1;i<=n;sta[++top]=i,i++)
while(top>=2&&Node(i,sta[top])-Node(sta[top],sta[top-1])<=eps) top--;
}
旋转卡壳
利用凸包上一些奇妙的单调性,求解
- 多边形直径
- 多边形宽度
- 最小面积矩形覆盖
- 等等
复杂度\(O(n)\)
for(int i=1,p=1;i<=n;i++)
{
//这份代码只卡了一个点,还可以同时卡多个点
while(H(A[i],A[i+1],A[p%n+1])>=H(A[i],A[i+1],A[p])) p=p%n+1;
Ans=max(Ans,max((A[p]-A[i]).dis(),(A[p]-A[i+1]).dis()));
}
最小圆覆盖
随机增量构造,复杂度\(O(n)\)
感觉可以被扁平三角形卡掉,但是实际上并不会,由于\(ijk\)的枚举顺序,三角形一定是在尝试把三条边都作为直径都失败后、才会有三角形的外接圆。(2019.2.23 byGXY)
pair<Node,Node> Line(int k,int i)//中垂线
{
Node a=A[k]-A[i];a.rot();
Node c=(A[k]+A[i])^0.5;
return mp(c,a+c);
}
int main()
{
random_shuffle(A+1,A+n+1);//先随机化
for(int i=1,j,k;i<=n;i++)
if((A[i]-C).dis()>R)//某点不在圆内,更新为半径为0的圆
for(C=A[i],R=0,j=1;j<i;j++)
if((A[j]-C).dis()>R)//某线段不在圆内,更新为以该线段为直线的圆
for(C=(A[i]+A[j])^0.5,R=(A[i]-C).dis(),k=1;k<j;k++)
if((A[k]-C).dis()>R)//某三角形不在圆内,更新为该三角形的外切圆
C=Cross(Line(k,i),Line(k,j)),R=(A[i]-C).dis();//求两条中垂线交点
}
自适应辛普森积分
用来求定积分。
当函数极其鬼畜、退不出原函数的时候,采用二次函数拟合,在精度达到要求之后便视为相等
即$$\int_LRf(x)dx\approx\int_LR(Ax^2+Bx+C)dx=\frac{(R-L)(f(L)+f(R)+4f(\frac{L+R}{2}))}{6}$$
double f(double x) {return (c*x+d)/(a*x+b);}
double calc(double l,double r) {return (r-l)*(f(l)+f(r)+4*f((l+r)/2))/6;}
double simpson(double l,double r,double ans)
{
double mid=(l+r)/2,ans1=calc(l,mid),ans2=calc(mid,r);
if(fabs(ans1+ans2-ans)<=eps) return ans;
return simpson(l,mid,ans1)+simpson(mid,r,ans2);
}
int main()
{
std::cin>>a>>b>>c>>d>>L>>R;
printf("%.6f\n",simpson(L,R,calc(L,R)));
}
注意\(\frac{1}{x}\)的原函数是\(ln|x|\)!!
三维凸包
出门左拐:https://www.cnblogs.com/xzyxzy/p/10225804.html
闵可夫斯基和
出门左拐第二家:https://www.cnblogs.com/xzyxzy/p/10229921.html
Pick定理、欧拉公式和圆的反演
出门左拐第三家:https://www.cnblogs.com/xzyxzy/p/10241872.html
Voronoi图与Delaunay三角剖分
出门左拐第四家:https://www.cnblogs.com/xzyxzy/p/10349403.html


 浙公网安备 33010602011771号
浙公网安备 33010602011771号