小白学高数 - 概念理解 - 无穷级数

无穷级数是什么呢？

无穷级数，简单来说，就是把无穷多个数相加求和。
但是这些数，是有顺序的，叫做数列。

---

什么是数列呢？

“列”就是排列，有顺序地排列，“列”强调的是顺序。所以，有顺序的一组数，就是数列。

---

数列有什么特点呢？
数列，可以是有规律的，也可以是无规律的；可以是有限多个，也可以是无限多个。

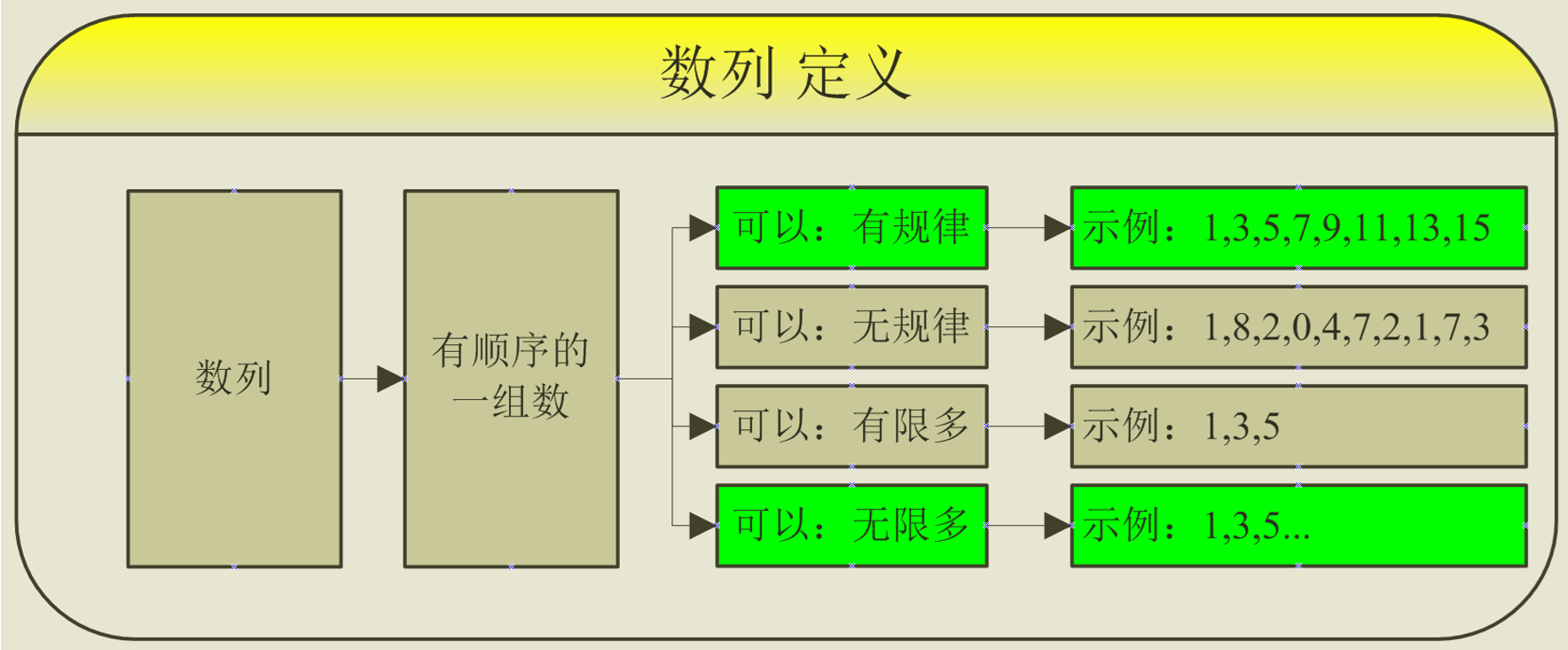
对于无规律的一组数：研究的时候无从下手，没规律还怎么研究？研究的意义就不大，跳过，不讨论。
对于有限多的数：就是简单的加法，相加得到一个固定的数值。这很简单，也没有什么可深入研究的，跳过，不讨论。

所以，对于有规律的、但是数量又无限多的数列的求和，就值得研究研究了，这个操作求和就是级数。

---

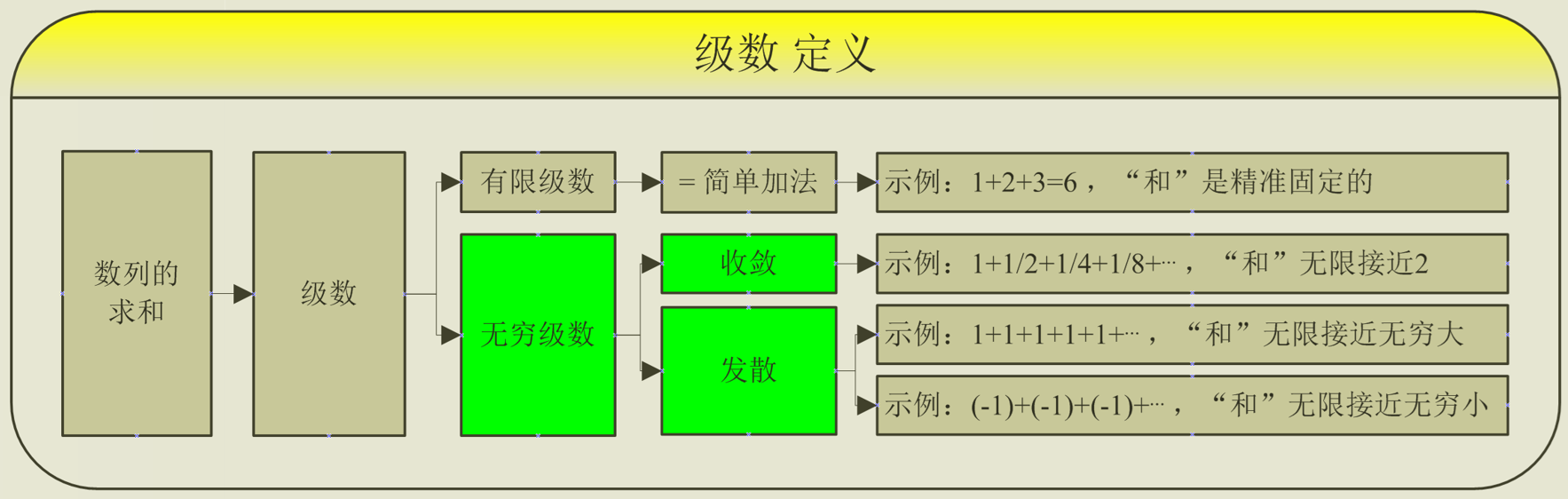
级数，就是一项一项的数累加，当有无穷多个这样的数相加，就是无穷级数。

级数加的项越多数字会越大吗？
不是的。有可能加的数是负数，这样会越加越小；也有可能加的数没什么规律，也不知道将会越大还是越小。

---

收敛

那么级数的变化到底有什么规律呢？

任何的相加操作求和，结果都可以分为三类：变大、变小，和不变。
对数列中的每一项加和，越加的后面，总和变化越小，给人一种加不动的感觉，不管怎么加，它都不给出大反应，像GA了一样，没什么动静，从数值结果上来看，就是越来越接近于某个具体的数值，这个现象就是“收敛”。

不要太嚣张
当一个人太嚣张的时候，我们会说，你赶紧收敛一下吧，你赶紧停一下吧，别这么嚣张了，所以“收敛”是助手、停止的意思。保持安静，不要动了。
对应到数值的描述，就表现为：越来越趋近于某个具体的数值。这个收敛的数值，一般是一个边界值，这在很多场景下非常的有意义，也就是无穷级数要研究的重点。

---

那么级数包含哪些情况呢？具体怎么分类呢？可以从不同的方面对它进行分类。
按照数列中每一项的正负，可以划分为：正项级数、交错级数、任意项级数：

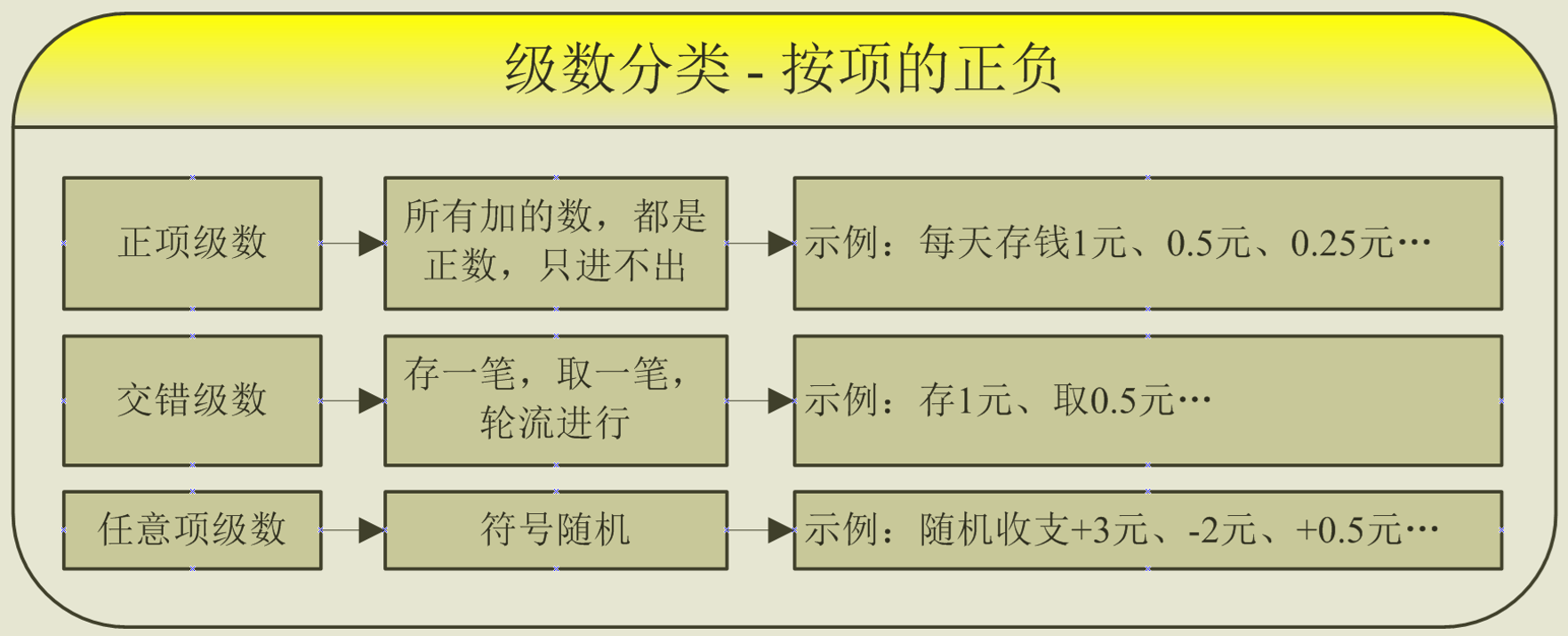
按照相加结果的收敛性，可以分为收敛级数，和发散级数：

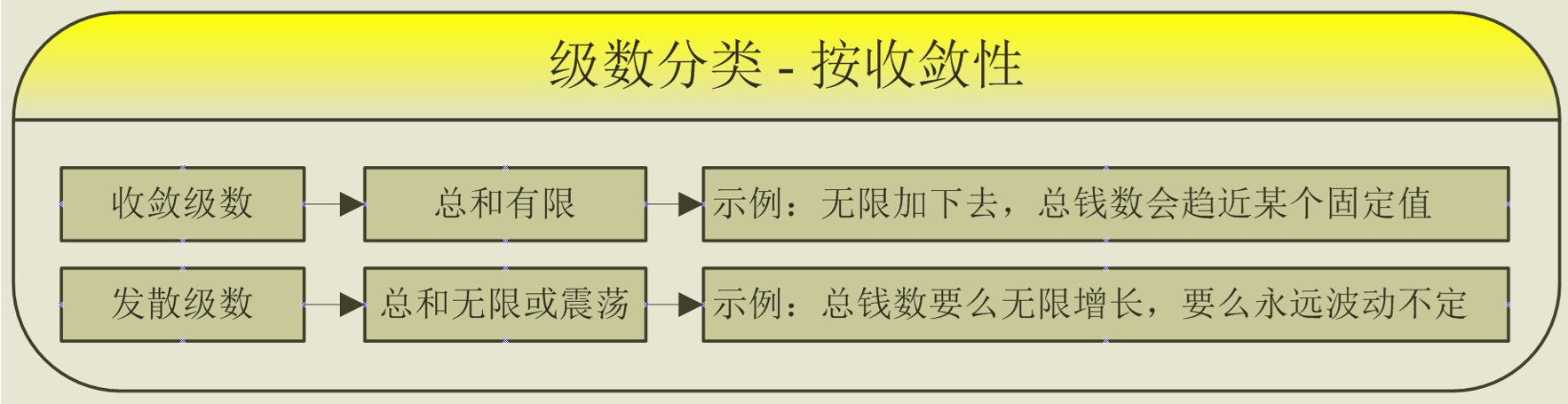
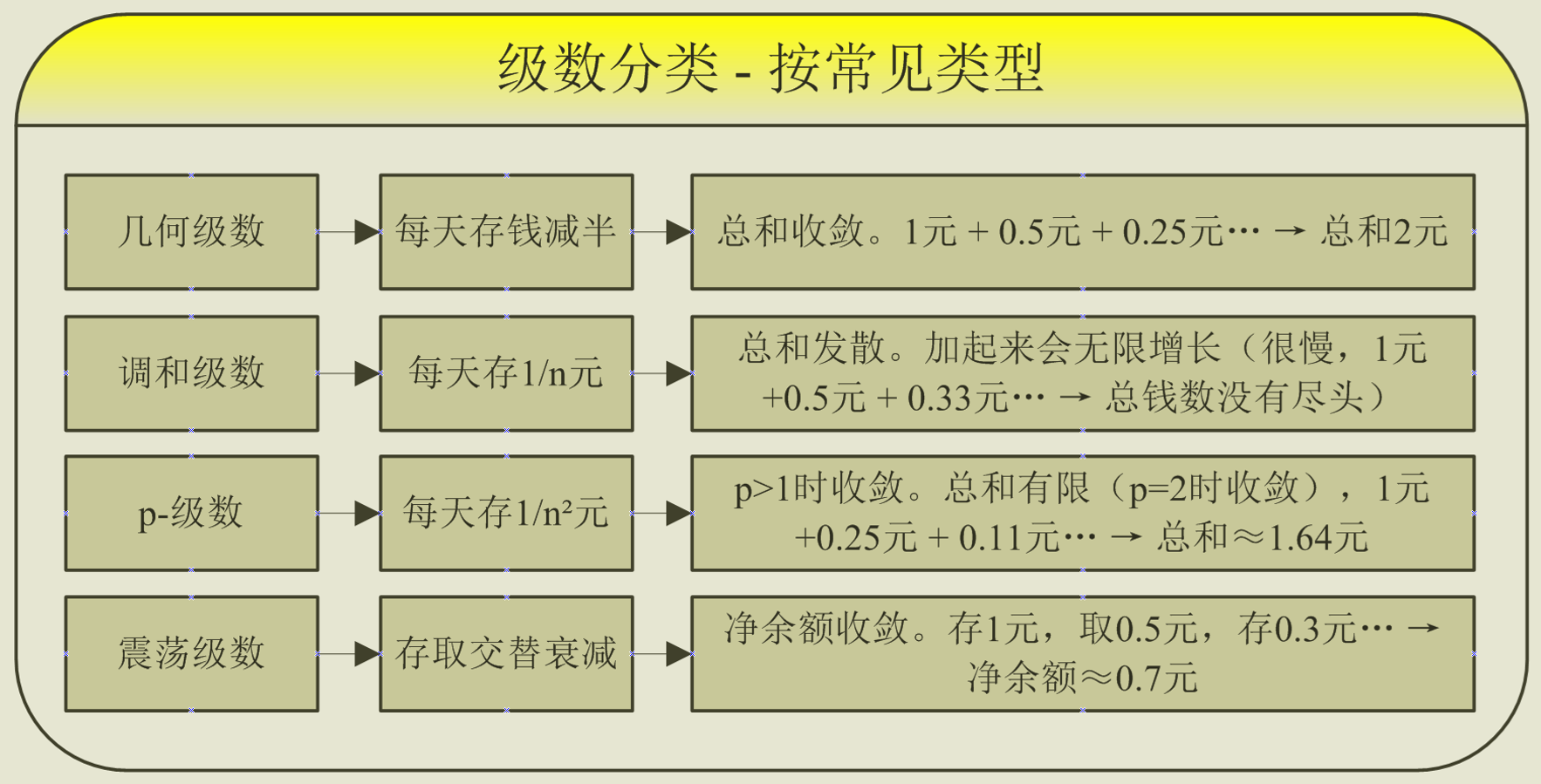
根据使用场景的常见类型，可以分为几何级数、调和级数、 p-级数，和震荡级数：

---

收获

在学习概念之前，以为无穷级数是对数进行无穷的分级，也在好奇为什么数也要分个三六九等的分级？不明觉厉。学习了之后了解到，它就是对数的相加，现在祛魅了。虽然流程图有一部分概念还没有完全理解，但是大致了解了它的意思和涉及的范围。

---

期待

本文是对 高等数学 第7版 下册 的最后一章从概念上的理解。前面先后对函数、极限、导数、微分、不定积分、定积分、向量代数、空间几何、重积分、曲线积分、曲面积分、无穷级数，进行了概念上的理解。
从下一篇开始，将要进入对我这个高数小白最具有挑战的事情：开始深入内部理解它的公式。为了更好地理解公式的运算过程，我会使用C#作为辅助工具，来可视化这个计算过程，这些像蚯蚓和天文一样的符号，我目前一个都看不懂，但是当我想到将要彻底地理解并掌握它们，这真的是一个令人兴奋的事情，非常的期待。