小白学高数 - 概念理解 - 曲线积分/曲面积分

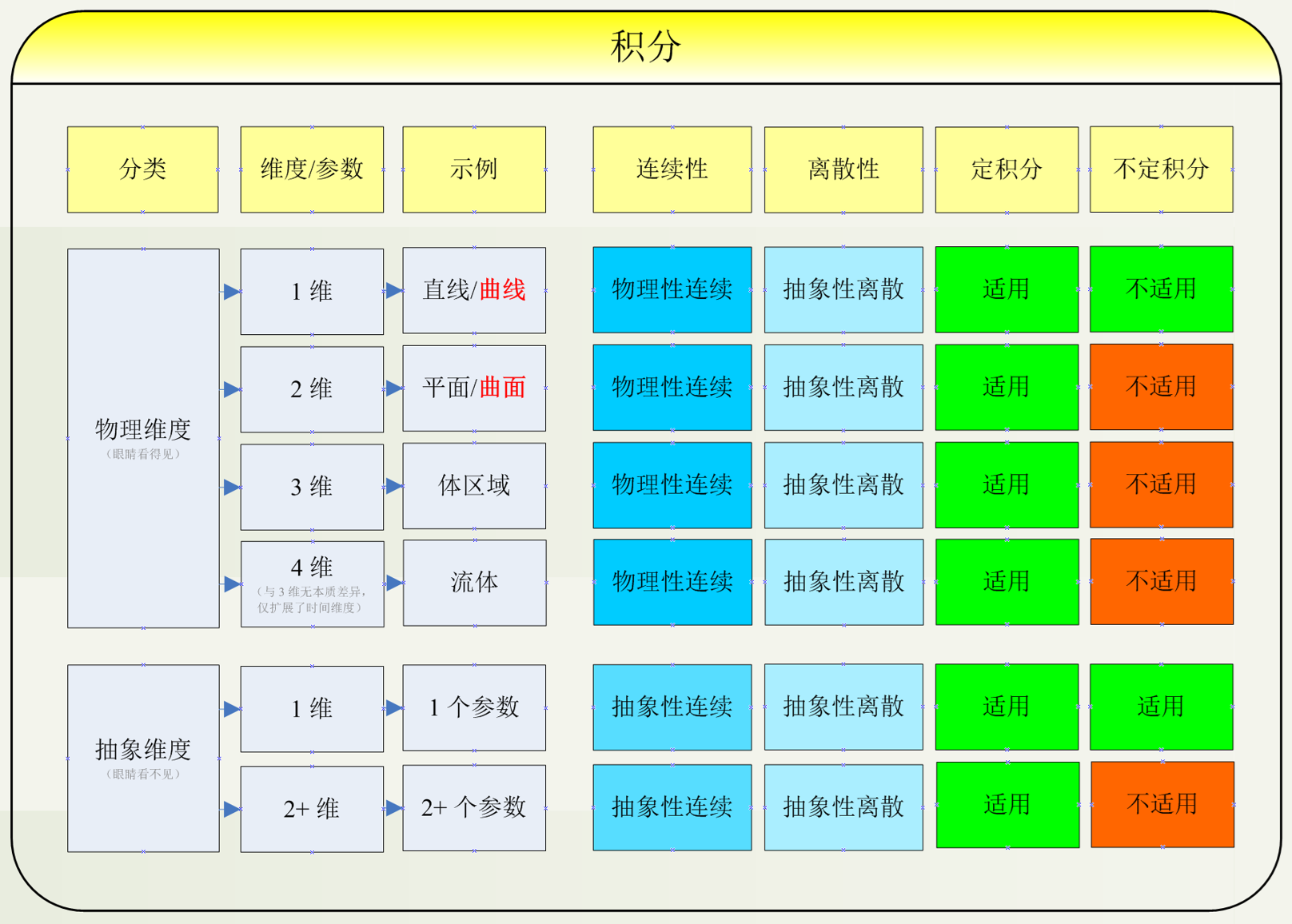
在前面学习积分的时候，我了解到，积分可以分为 定积分 和 不定积分，这是从计算过程的角度来区分；那么现在我们要对积分进行 维度 的区分。
通过解答以下几个疑问，来学习本文 曲线积分、曲面积分。

---

问：前面不是学习了积分，可以划分为 定积分 和 不定积分 吗？现在怎么又要区分 曲线积分 和 曲面积分？

答：定积分 和 不定积分 ，是从计算过程的角度来区分的；曲线积分 和 曲面积分，是从积分的维度上来区分的，也就是积分的参数个数来区分的。曲线积分，属于一维积分，曲面积分，属于二维积分。

---

问：现在提到了一维积分，二维积分，那么还有其他更多维度的积分分类吗？都可以对什么进行积分呢？

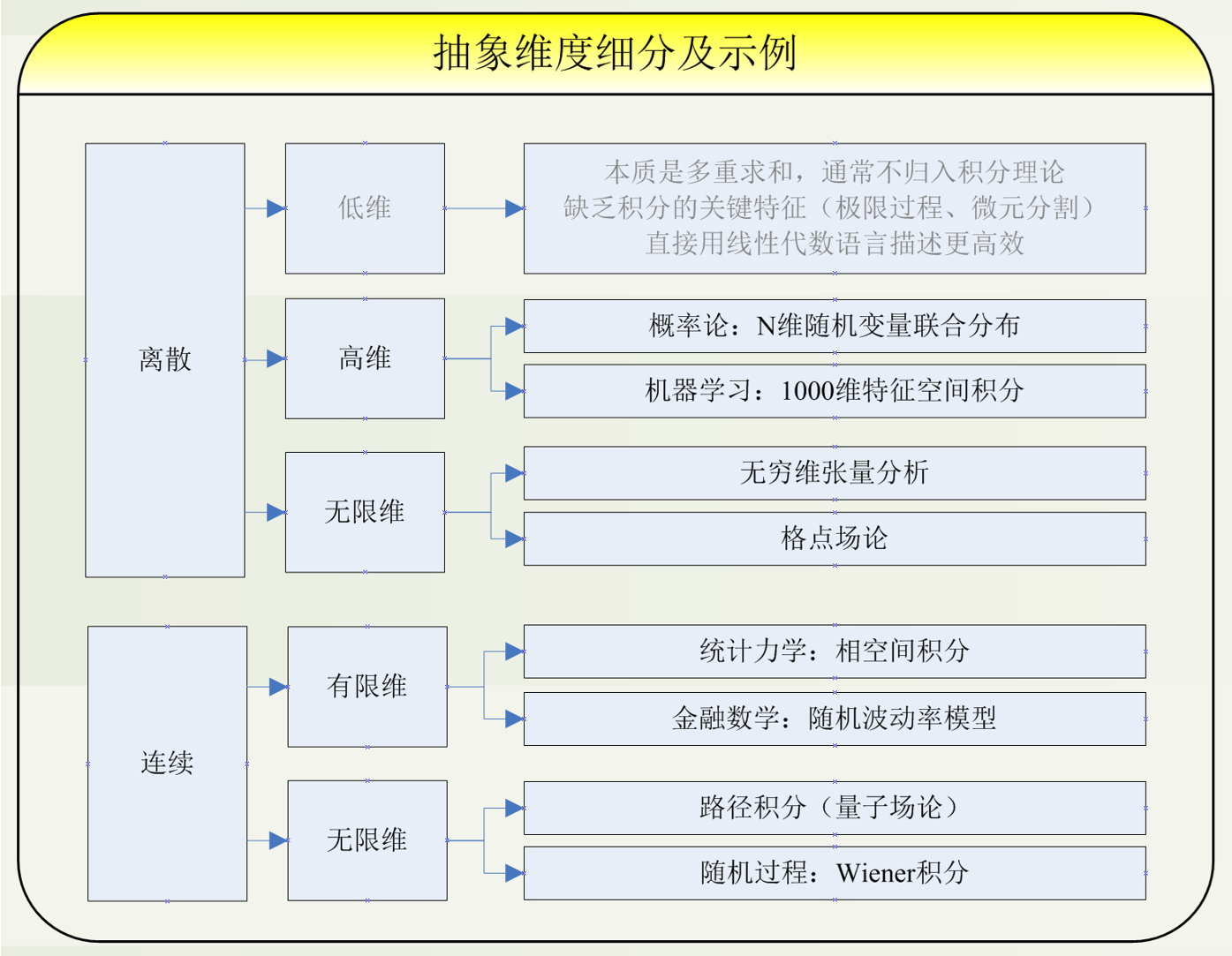
答：不仅可以对眼睛看得见的、物理维度进行积分，也可以对眼睛看不见的、抽象维度进行积分。对眼睛看得见的物理维度，最多划分为三维，一维的包含：直线和曲线；二维的包含：平面和曲面；三维的，就是指的是体区域；这里还有个四维，但是它与三维没有本质的差异，是在三维的基础上添加了一个时间的维度，叫做流体。 对眼睛看不见的抽象维度，可以从一维，扩展到任何高维，以及无限维。

---

问：不管是物理维度还是抽象维度，都可以进行 定积分 吗?

答：是的。定积分 适用于任何分类的任何维度。

---

问：不管是物理维度还是抽象维度，都可以进行 不定积分 吗？

答：不是的。对于 物理维度 或者 抽象维度 的一维，都可以进行 不定积分； 但是2+ 维度都不能 不定积分。

---

问：对于眼睛可见的物理维度的分析，是进行的连续性计算？还是离散性的计算呢？

答：可见的、物理性的三个维度，本身就具有连续性，这属于传统的积分范畴 ；但在实际计算时，有可能会将他们进行 离散处理，进行数值范畴的计算。

---

问：对于眼睛不可见的抽象维度的分析，是进行的连续性计算？还是离散性的计算呢？

答：抽象维度，它本身不具有连续性，既可以把它按照离散性处理，也可以近似地模拟为连续性处理。
那么回到本节我们要讲的重点，根据积分的分类及特性，汇总了文首的分类图，此时我们知道了曲线积分和曲面积分在我们研究的整个范围中所处的位置（红线勾选的部分）。

---

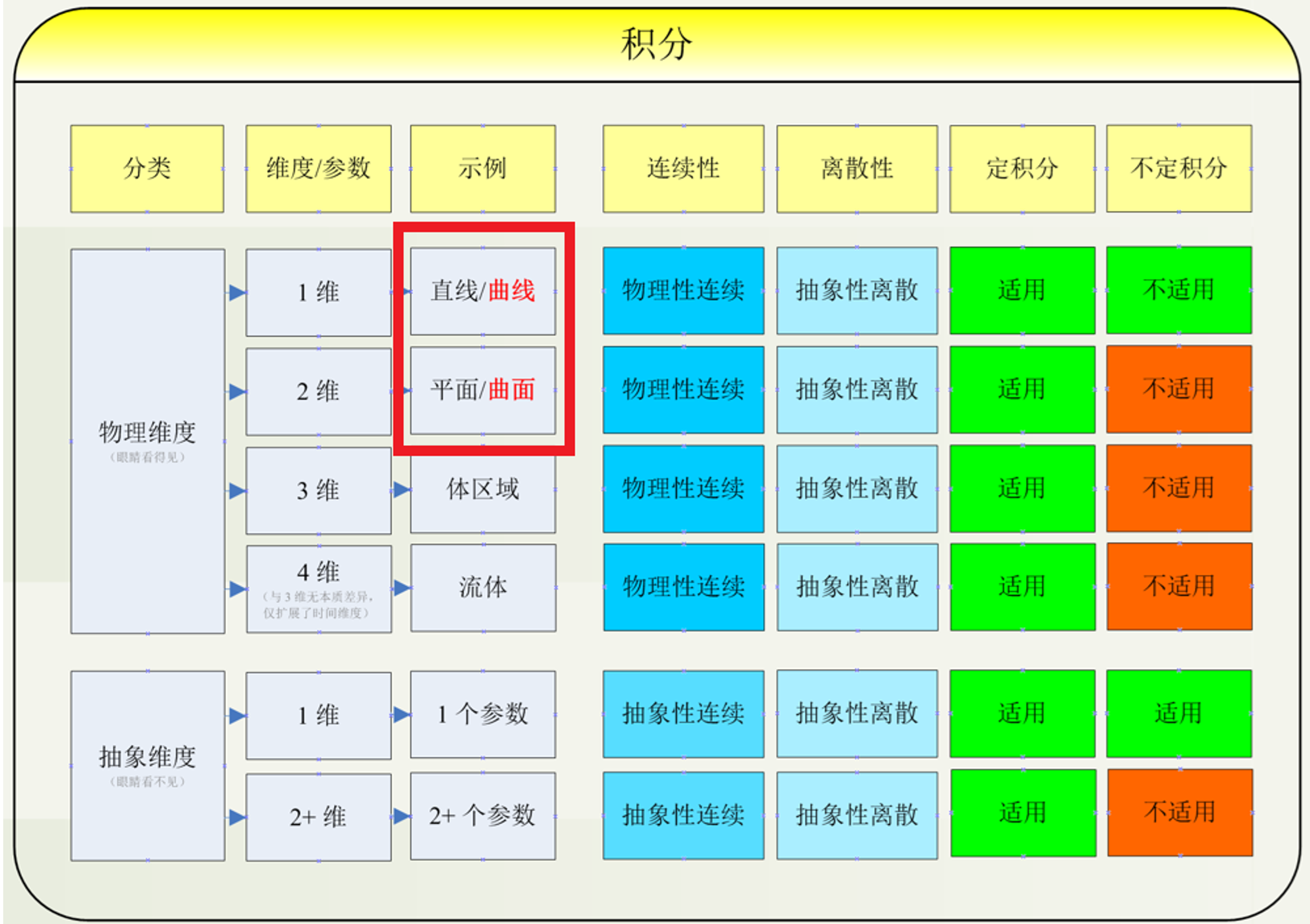
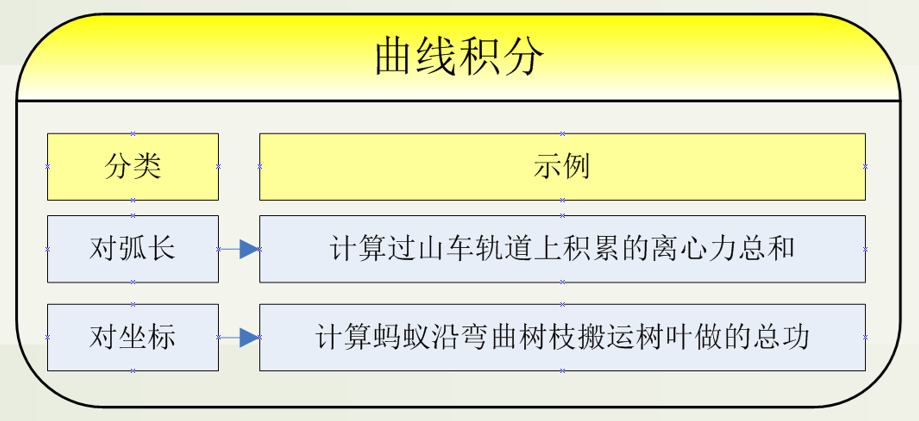
现在我们来理解 曲线积分 就比较容易。

定义：在"弯曲的路径"上积分。
相当于 ：沿着铁丝，测量铁丝上的属性累积

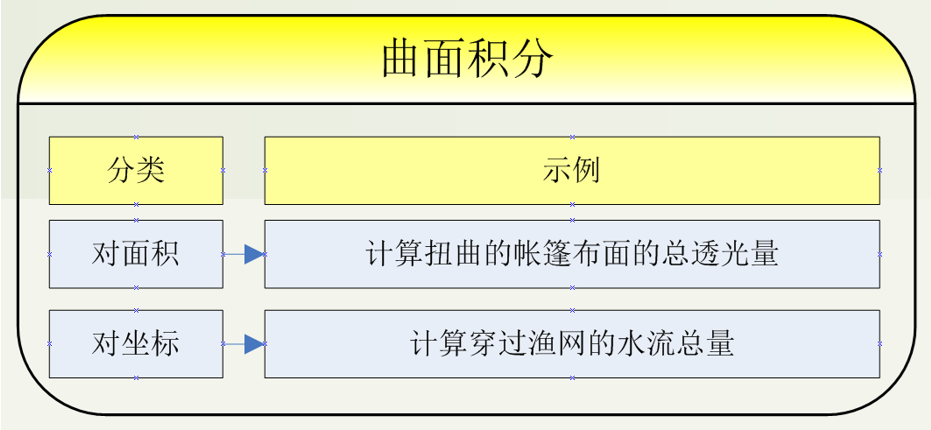
曲面积分：

定义：在"扭曲的膜"上积分。
相当于 ：覆盖薄膜，测量薄膜上的属性总和

---

最大收获

通过以上的学习，最大的收获不在于学了2个新概念，而在于明白了曲线积分和曲面积分两个概念在整个积分分类框架中的位置，更清晰了它们可能在解决实际问题过程中的一些所属范畴。