小白学高数 - 概念理解 - 向量代数

定义

有方向的量，代入数值进行计算，即 向量代数

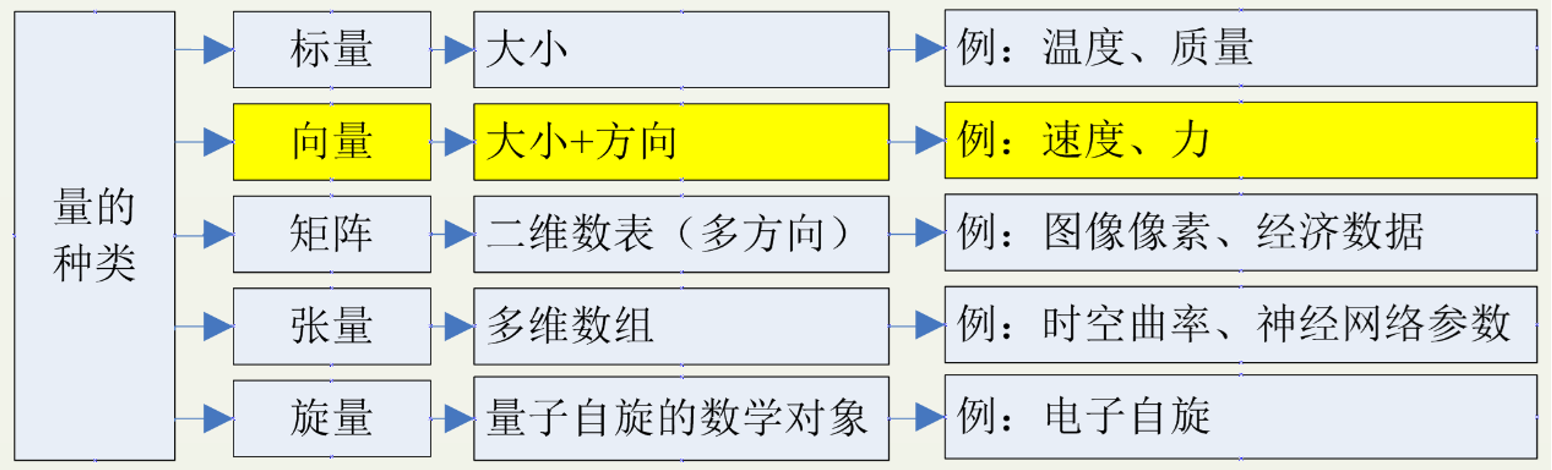
那么，除了有方向的量，还有哪些种类的量呢？我们研究的向量在哪个范围中呢？
还包含标量（大小）、向量（大小+方向）、矩阵（二维数组）、张量（多维数组）、旋量（量子自旋）等。

---

递进式理解

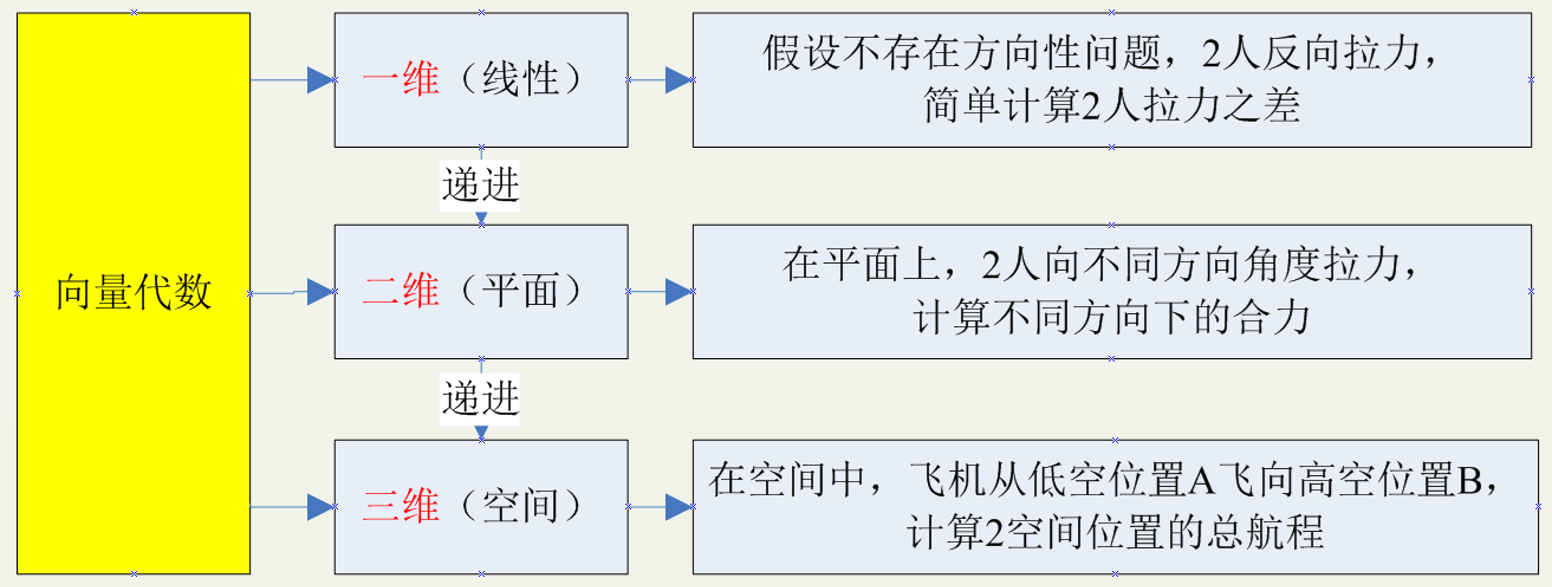
一维：小学的时候老师讲到，在同一个方向上，小明向 东 使用 5 牛的力，小强向反方向 西 使用 3 牛的力，那么结果会偏向东多少力？这是简单的减法计算：5-3=2；
在此处，实际上假设了不存在 方向性 问题，所以代入 5 和 3 两个简单的数字，就得到了 2 这个数值，这是 一维 的计算，它是 平面向量代数 的一种特例；
二维：在实际问题中，我们会遇到各个方向的问题，比如向 前方 走500米，再向 左边 走500米，那么相当于我们向 左前 方走了多少米？这是二维的计算，它是 空间向量代数 的一个特例；
三维：更复杂的，要考虑到三维空间方向，在立体空间上的方向变化的一些量的计算，比如 飞机从低空的位置A飞向高空的位置B，飞行的总航程计算；

---

研究视角

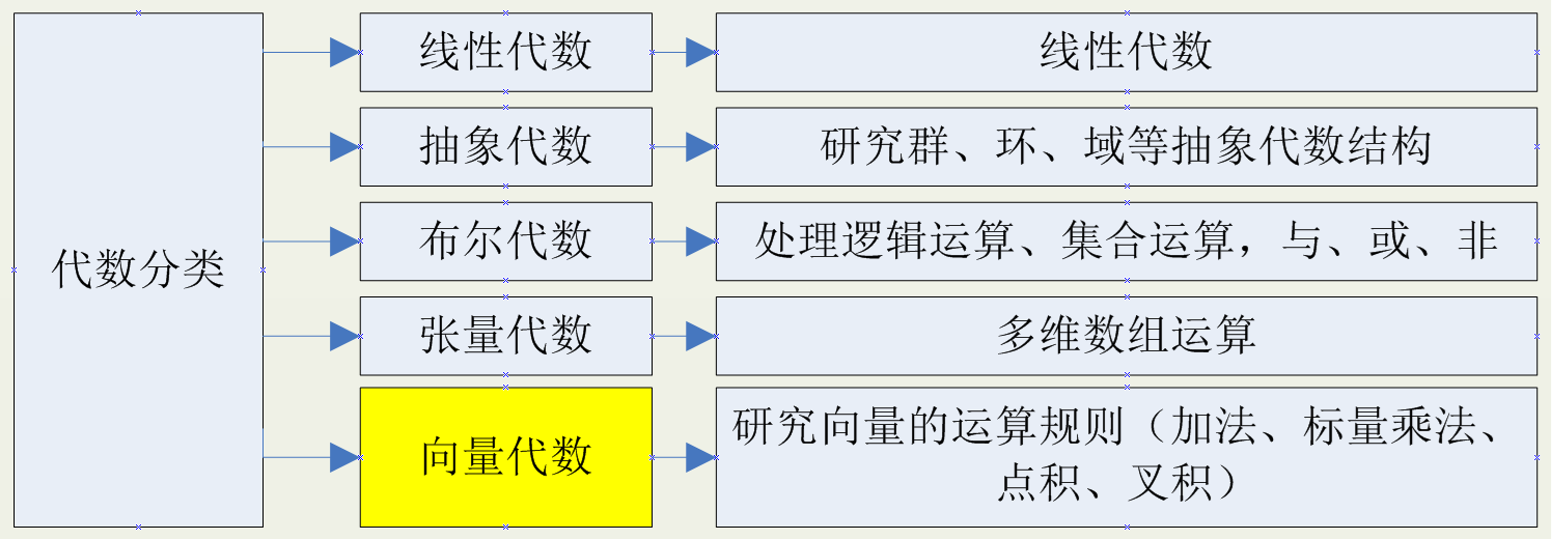
那么向量代数是我们研究问题中的哪一个视角呢？除了向量代数，还有什么代数呢？
还有线性代数、抽象代数、布尔代数、张量代数等：

---

解决问题

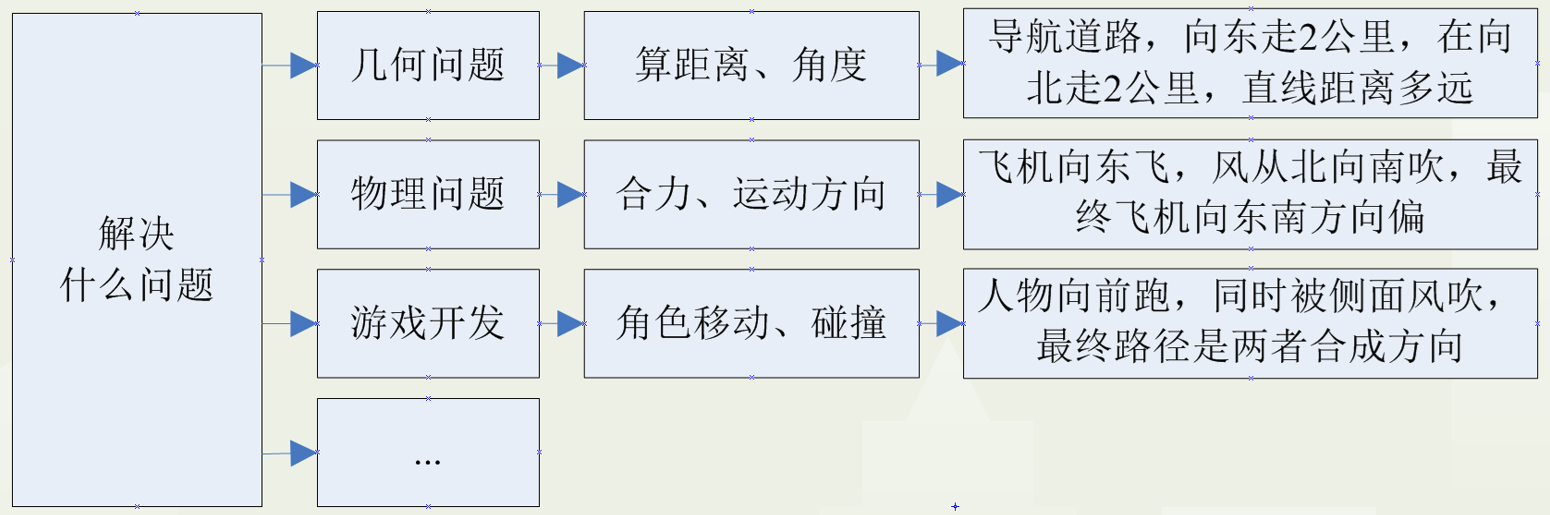
向量代数可以解决什么问题呢？
几何问题（算距离、角度）、物理问题（合力、运动方向）、游戏开发（角色移动、碰撞）等等。

---

浪漫总结

万物皆可向量代数。
你是东向的晨曦，我是北向的溪流，遇见你后，我们合成独一无二的轨迹 -- 斜阳下的漫步方向.