小白学高数 - 概念理解 - 积分

---

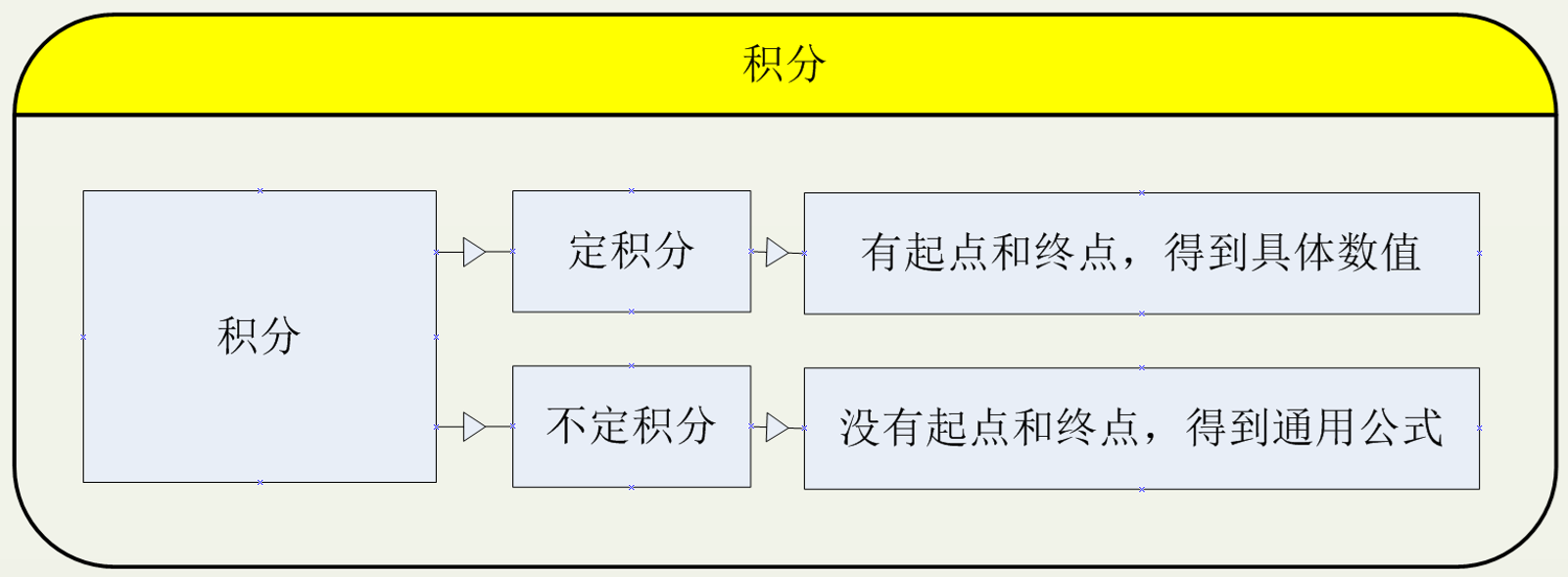
定积分与不定积分
积分，分为 定积分，和不定积分。

定积分：可以理解为，在固定总范围内，把一个规律性的事物，划分为无限份数，并进行累积的过程。就好像：在一个空的存钱罐里面，每天存入一块钱，连续存储30天，最后得知总共存储了30块钱。
不定积分：可以理解为，对于一个未知的目标范围，把一个规律性的事物，划分为无限份数，并进行累积的过程。就好像：男朋友送了一个存钱罐，里面已经有了一些钱，但是为了保持神秘感，他不告诉我，然后接着我自己每天往里面存一块钱，存储了30天，由于不确定最初里面有多少钱， 所以它的总钱数是 X+30, 这里的X就是男朋友送给的充满了浪漫甜蜜的无限可能。

---

积分与加法

加法计算：

积分计算：

积分，与加法，有相似之处，由上面两个比对，看到加法与积分的最大的区别是:
加法：绝对准确性，需要依赖于对这段圆弧的绝对的准确的计算，
积分：近似相等性，只需要对这段近似圆弧的直线的进行近似相等计算。
积分的必要性：当已有的计算条件非常的有限，并且需要高效地计算的时候，定积分就显得非常的必要；但是实际计算的时候，划分的段数是尽可能多份的，或者无限多份的，这样才能达到更高的精准度

---

积分的现实意义
把以上区别反映到实际的场景中，表现是，
加法：要求对每一个小份数有严格的标准的完全精准的计算方式，它的要求过于严格和苛刻，
积分：对于每个小份数的计算，只需要近似相等就可以，要求比较低，更容易得到，在实际场景中落地的可能性会更大，因此更实用；

这两者都能满足条件的情况下，那绝对是用加法是更准确的，但是当现实的条件更复杂的时候，一般是不具备这个条件的，只能退而求其次来分为小份数计算个大概，再累积。

---

积分 Q&A

切割份数必须等长吗？
• 不是的，也有可能会划分为不同的小区域，每个小区域内进行不同尺度的计算来进行累积；
每小份的结果必须相同吗？
• 不是的，不同小区域的计算参数可能不同，而得到不同的结果数据作为累加；
仅仅是直线的数值相加计算吗？
• 不是的，实际可能是各种其他形式，面积、趋势图等；
如何得到要切割为多少份数？
• 实际上的切割份数远比示例图中的份数更多，理论上需要让他接近无限小，但是这个粒度的最合适的一个值的查找，需要考虑到规律的连续性和规律的稳定性，基本上在确保规律的稳定性的前提下，就不必要再继续进行更细的划分，够用即可。

---

积分的爱情哲学
积分是对加法的妥协，是对不完美的妥协，类似于：如果我不是你，那么我就无限的接近你，这是我成为你的唯一的最近的方式；
如果加法是完美主义，那么积分就是实用主义，如果不能达到极致完美，那么就做到极致实用，它虽然不是100%的完整，但是也已经做到了在它极限范围内的完美。
这难道不是一种执着的爱情哲学吗？

我想抵达你，但是请原谅我，我已经尽力 ~