最远点采样加速---QuickFPS
一、背景
最远点采样FPS算法是下采样方法中应用最广泛的技术,能够尽可能保留原始的空间特征。先前的研究已经证实,在大规模点云处理中,FPS的性能优于随机采样。然而,FPS的计算量过大,必然会成为整个流程的瓶颈。在各个常见的点云网络中发现当16384个输入点进入神经网络(NN)时,30%-70%的运行时间都用于FPS处理。
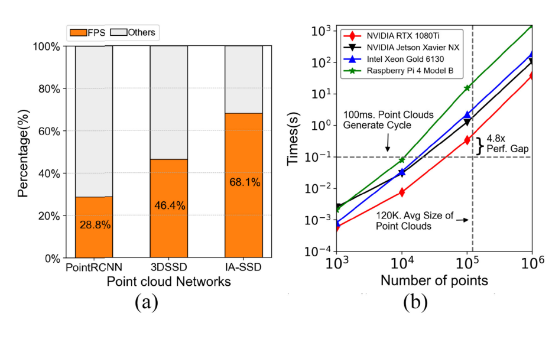
FPS由两层循环构成,其内层循环对计算并行性要求很高。最常见的解决方案是使用高端GPU来处理FPS,但遗憾的是,当点云规模扩大时,精度会出现显著差异。
在本研究中,我们尝试使用高规格GPU对10⁶规模的点云进行FPS采样,抽取其中10%的点。我们发现大部分计算都消耗在内存事务中,主要原因是内存占用量过大。特定领域的硬件加速器可以通过协同设计的架构和算法来弥补性能差距。目前已有多种用于点云处理的硬件加速器被提出。
然而,目前唯一针对FPS的加速器是PointAcc。
PointACC由MPU、MMU和 systolic carriage 组成的6级流水线构成,它能够同时计算多个点到最新采样点的距离,并构建了一个“获取-计算-排序”流水线,以优化片上存储器访问和计算操作。尽管PointAcc是一种能提高性能的高效架构,但它存在内存占用量大的问题。PointAcc不适用于大规模点云。因为当点云的规模超过加速器的片上容量时,PointAcc需要在片上静态随机存取存储器(SRAM)和片外动态随机存取存储器(DRAM)之间频繁交换数据,这会导致不可接受的延迟。
为解决上述问题,提出了QuickFPS。
二、核心思想
这一篇介绍的QuickFPS采用两级树算法将大规模点云划分为多个点桶,然后,根据空间和几何特征,只处理少量必要的桶。最后,为了最大限度地发挥基于桶的FPS的优势,对部分桶内点距离进行延迟更新,并协同设计加速器,是一种高效的FPS处理算法。

三、相关细节
3.1 距离更新
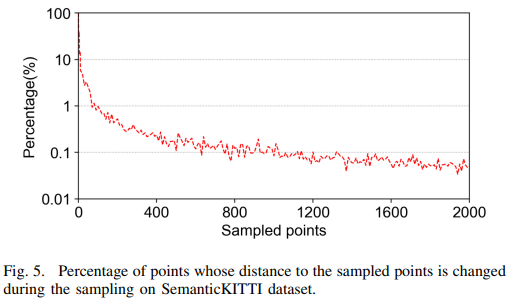
我们开展了一项案例研究,以展示在采样过程中其到采样点的距离被更新的点所占的比例。在该案例研究中,FPS采用了SemanticKITTI[32]数据集,该数据集平均包含120000个点。我们对2000个点进行了采样。如图5所示,在开始的400次迭代中,这一比例从100%迅速下降到1%以下。1200次迭代后,该比例甚至下降到0.1%以下。这一结果表明,在大多数迭代中,只有少数点需要更新距离。如果某个桶满足特定条件,就可以省去对该桶内点的内存访问。
3.2 树构建
采用kdtree将点云划分成块,构建一个两层树。Kd树是一种二叉树,按最大范围内的维度对点进行排序分成两组,重复分割过程,直到创建出所需数量的桶。它将点云空间划分为小区域。每个块维护一个最远点,通过少比较和延迟更新来加速。
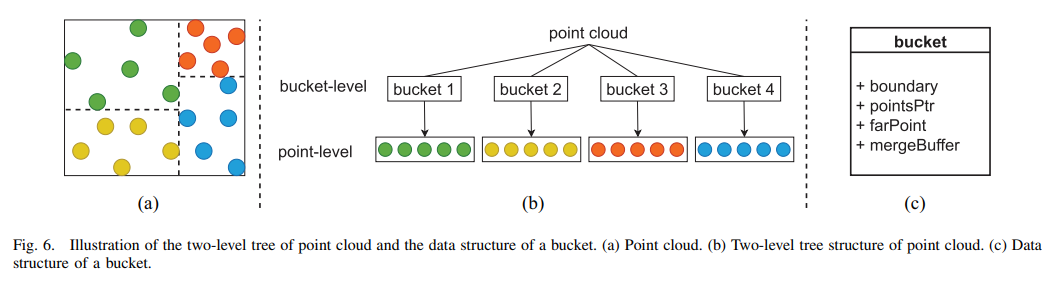
- 桶的结构体
| 变量 | 含义 |
|---|---|
| boundary | 边界:包含桶的最小和最大坐标 |
| pointsPtr | 点指针:包含当前桶的点数据在DRAM中的起始地址 |
| farPoint | 远点:表示数据包中点中距离采样点最远的点 |
| mergeBuffer | 合并缓冲区:存储需要在后续迭代中处理的采样点 |
-
符号定义

-
桶远点
给定一个采样点集S_k、一个桶B_i和点云P。桶远点被定义为桶内距离S_k最远的点。
由于FPS会选择最远的点作为采样点,下一个采样点将从桶远点中选取。
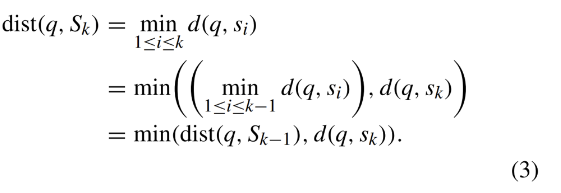
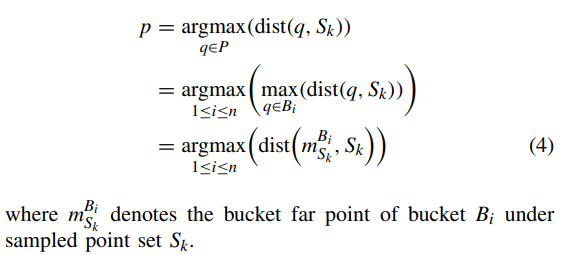
计算每个桶内点q与S_k的最大值,并返回采样点集S_k与该桶的桶远点之间的距离中的最大值以及S_k。
3.3 跳过更新距离的情况
依据公式3可知当最新采样点距离如果大于之前的点距离,则该点的距离是不需要更新的
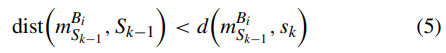
如果将公式5代入公式3,若dist()小于d(),则\(dist(m^{B_i} {S {k-1}},S_{k-1})\)就等于\(dist(m^{B_i} {S {k-1}},S_{k})\)
因此,在\(S_{k-1}\)下桶b_i的远点与在S_k下的远点相同。这个时候该桶的最远点不需要更新。
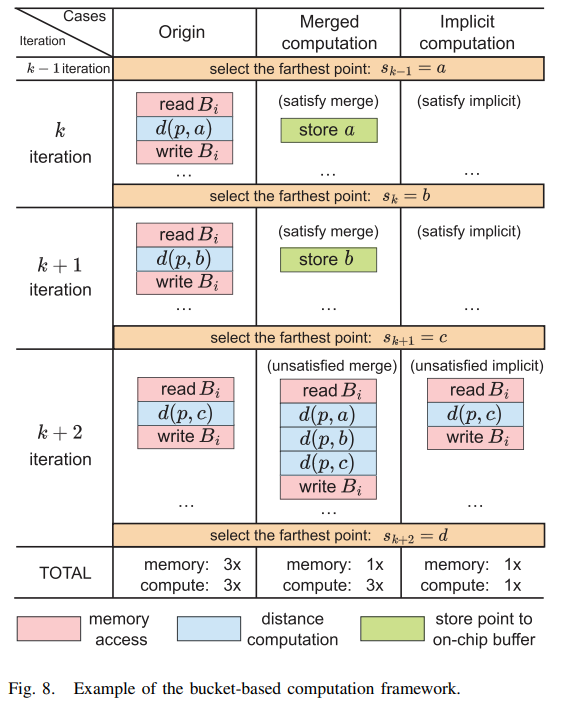
3.4 合并计算
通常,要得到下一个采样点\(S_{k+1}\),需要获取每个桶的桶远点\(m_{sk}^{bi}\),并从中选出最远的点。
然而,如果满足公式5,就会延迟对桶B_i的计算,因为只有当边界距离小于最远点距离,说明可能会影响到桶内的点距离,这种情况下是需要对桶内点进行检查看是否需要更新距离的,此时会将最近的采样点发送到合并缓冲区,后续达到一定数量后统一进行计算。
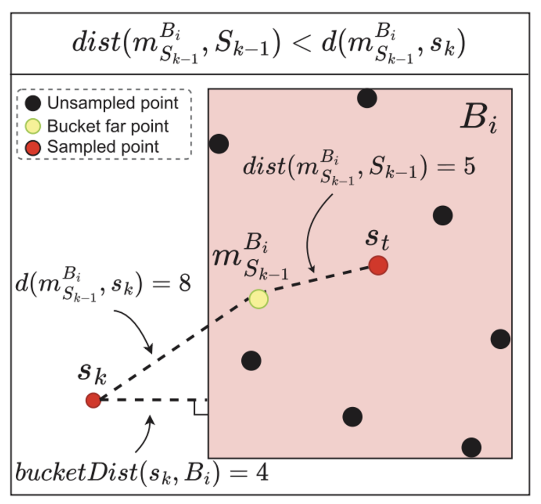
3.5 隐式计算
最新一个采样点距离桶中的所有点都很远,距离度量的距离不会发生变化。在这种情况下,可以跳过距离计算。
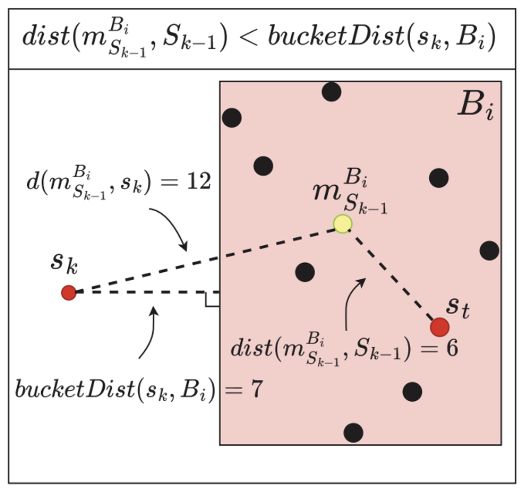
3.6 实现步骤
##### 更新流程(在KDNode::update_distance中):
1. 遍历等待点:对每个在waitpoints中的参考点:
• 计算当前桶的最远点(max_point)到参考点的距离cur_distance。
• 与桶内当前最大距离lastmax_distance比较:
• 如果cur_distance > lastmax_distance:说明参考点在当前桶的远处,只有当包围盒距离小时才可能影响桶内点的距离,进入下一步包围盒判断。
• 否则,说明参考点会影响当前桶的最大距离,即桶内存在点需要更新距离,将参考点加入delaypoints(延迟更新队列)。
2. 包围盒剪枝:
• 计算参考点到桶包围盒的最小距离boundary_distance。
• 如果boundary_distance < lastmax_distance:说明桶内可能存在点需要更新距离,将参考点加入delaypoints(延迟更新队列)。
• 否则,跳过该桶。
3. 批量处理延迟点:
• 当delaypoints中的点数达到阈值(MERGESIZE),则批量处理:
• 遍历桶内所有点,计算每个点到所有延迟参考点的距离,并更新点的最小距离。
• 更新桶的max_point(当前最远点)。
• 清空delaypoints。
4. 立即更新:
• 如果桶是非叶子节点,则将参考点下发到左右子节点(递归更新)。
• 如果是叶子节点且不满足延迟条件,则立即更新桶内所有点到参考点的距离,并更新max_point。
5. 清空等待队列:
处理完所有waitpoints后清空。
6. 最远点查找
在KDLineTree::max_point中:
• 遍历所有桶(KDNode_list)。
• 比较每个桶的max_point.dis(桶内当前最远点的距离)。
• 返回全局距离最大的点。
部分代码
void KDLineTree::sample(const int sample_num) {
Point ref_point;
for (int i = 1; i < sample_num; i++) {
ref_point = max_point();
sample_points[i] = ref_point;
update_distance(ref_point);
}
}
void KDLineTree::update_distance(const Point &ref_point) {
for(const auto& bucket : KDNode_list){
bucket->send_wait_point(ref_point);
bucket->update_distance(memory_ops, mult_ops);
}
}
void KDNode::update_distance(int &memory_ops, int &mult_ops) {
for(const auto& ref_point: this->waitpoints){
float lastmax_distance = this->max_point.dis;
float cur_distance = this->max_point.distance(ref_point);
mult_ops++;
// cur_distance > lastmax_distance意味着当前Node的max_point不会进行更新
if (cur_distance > lastmax_distance) {
float boundary_distance = bound_distance(ref_point);
mult_ops++;
if (boundary_distance < lastmax_distance) {
this->delaypoints.push_back(ref_point);
#ifdef NOMAPPING
#ifndef MERGESIZE
#define MERGESIZE 4
#endif
if(this->delaypoints.size() >= MERGESIZE){
//logging(this->idx, pointRight - pointLeft);
float dis;
float maxdis;
for (const auto &delay_point: delaypoints) {
maxdis = -1;
for(int i = pointLeft; i < pointRight; i++){
dis = points[i].updatedistance(delay_point);
if (dis > maxdis) {
maxdis = dis;
max_point = points[i];
}
}
}
this->delaypoints.clear();
}
#endif
}
}
else {
if (this->right && this->left) {
if(!delaypoints.empty()){
for (const auto &delay_point: delaypoints) {
this->left->send_delay_point(delay_point);
this->right->send_delay_point(delay_point);
}
delaypoints.clear();
}
this->left->send_delay_point(ref_point);
this->left->update_distance(memory_ops, mult_ops);
this->right->send_delay_point(ref_point);
this->right->update_distance(memory_ops, mult_ops);
updateMaxPoint(this->left->max_point, this->right->max_point);
} else {
//logging(this->idx, pointRight - pointLeft);
float dis;
float maxdis;
this->delaypoints.push_back(ref_point);
for (const auto &delay_point: delaypoints) {
maxdis = -1;
for(int i = pointLeft; i < pointRight; i++){
dis = points[i].updatedistance(delay_point);
if (dis > maxdis) {
maxdis = dis;
max_point = points[i];
}
}
}
mult_ops += delaypoints.size() * (pointRight - pointLeft);
memory_ops += (pointRight - pointLeft);
this->delaypoints.clear();
}
}
}
this->waitpoints.clear();
}
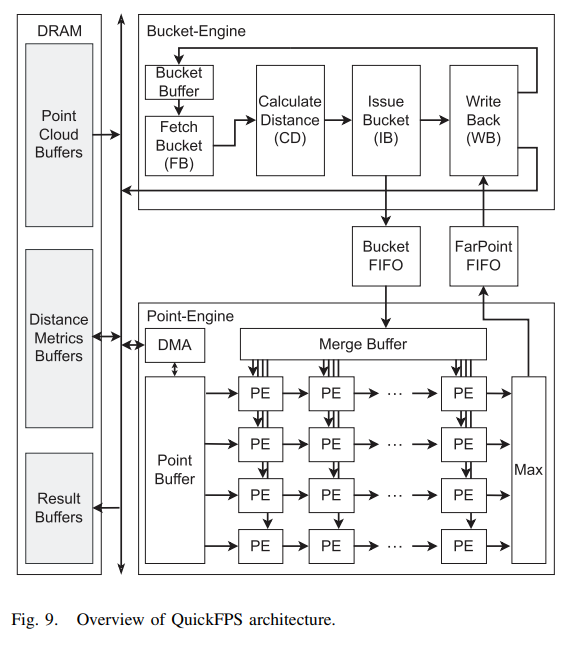
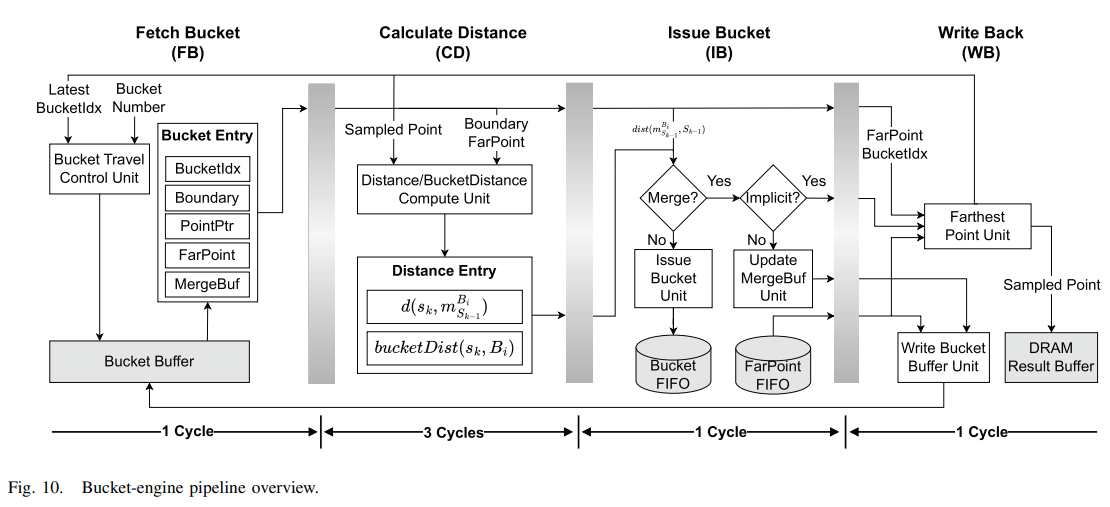
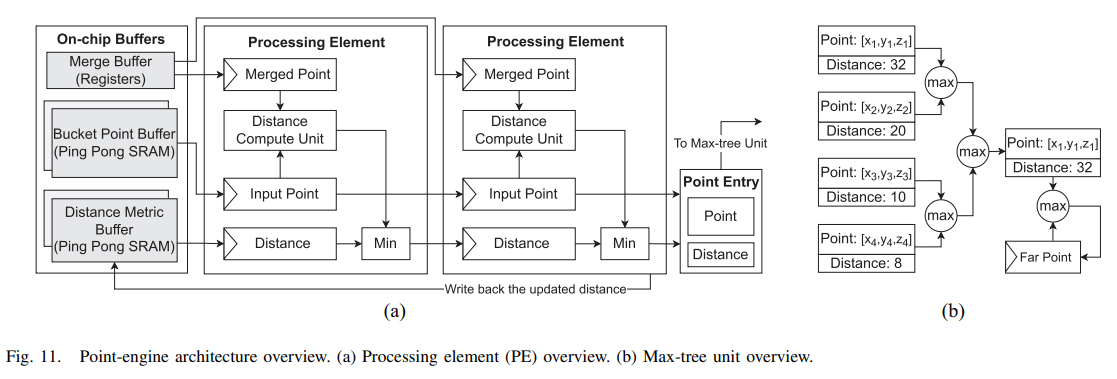
3.6 硬件加速
这一块主要是硬件加速,旨在最大限度地发挥上述机制的优势。这一块不太懂,直接把论文的图放这里了。
四、效果
-
性能分析
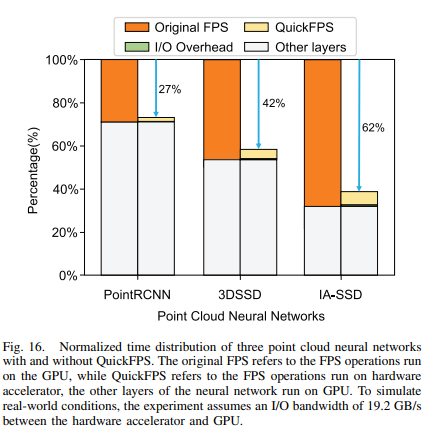
-
对比分析
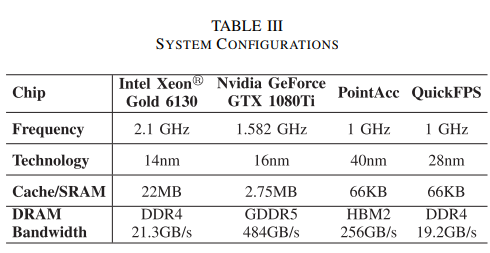
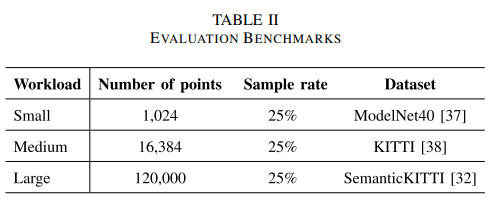
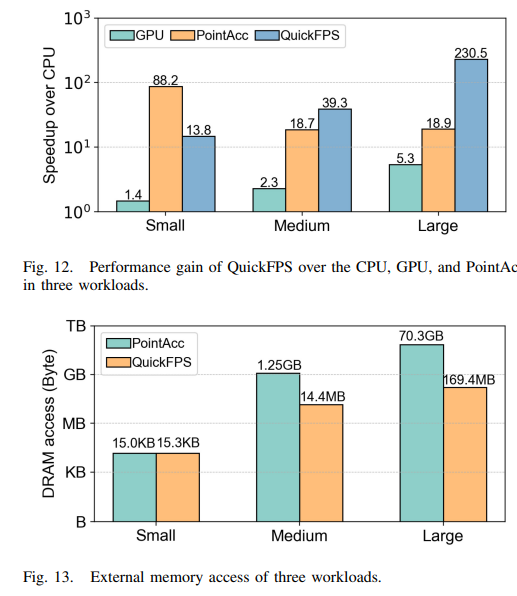
-
实测效果

在CPU上从91496个点中采样22874个点需0.17s,相比于之前的FPS(3.3s)和AFPS(0.25s)都要快,而且相比于APFS误差更小一些。
参考链接:
https://jisoo0-0.github.io/논문리뷰/2023/08/01/논문리뷰-QuickFPS.html
https://www.ablesci.com/assist/detail?id=E7KW1w




 浙公网安备 33010602011771号
浙公网安备 33010602011771号