斜框IOU实现

在目标检测时通常需要计算包围框的IOU，用于判断正负样本以及后续NMS过滤。框A和框B的IOU的值为其交集面积除以并集面积，

$$IOU = \frac{Area_{A \cap B}}{Area_{A \cup B}}$$

如果框为轴向包围盒，则可以参考IOU及NMS实现 ，但有时会遇到旋转框问题，这里对旋转框IOU计算方法做一个记录。

一、算法思路

参考论文 RRPN中提出的旋转框IOU计算方法

输入输出

• 输入： 由$(x, y, w, h, \theta)$表示的一系列矩形，其中$(x, y)$表示框的中心坐标，$w$表示框的宽度，$h$表示框的高度，$\theta$表示框由轴向包围框顺时针旋转至当前位置的角度。
• 输出： 任意两矩形之间的IOU值

算法步骤

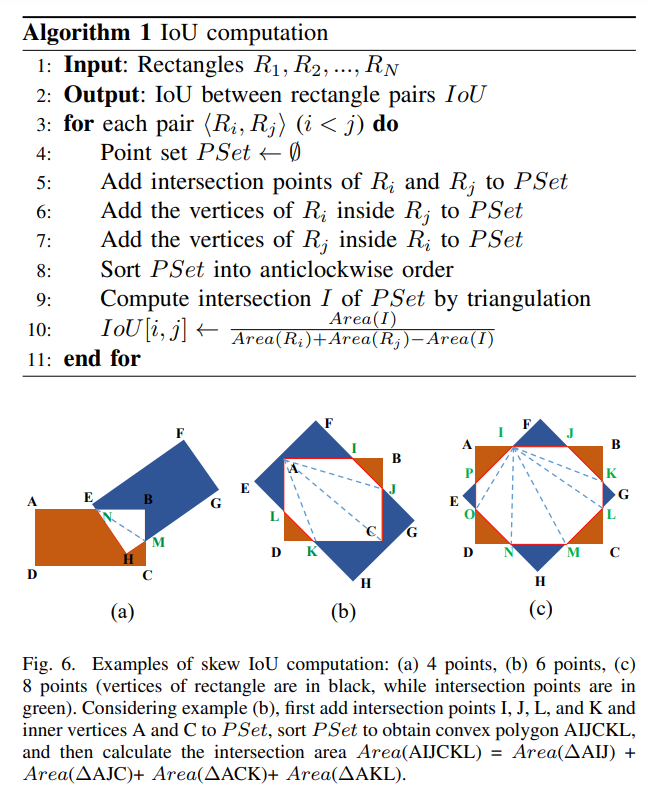
对于任意两个四边形$A$和$B$，其IOU计算如下：

• 将四边形$A$和$B$边的交点存于点集$P_{set}$
• 将$A$落在$B$内部的顶点存于点集$P_{set}$
• 将$B$落在$A$内部的顶点存于点集$P_{set}$
• 对点集$P_{set}$中点按照逆时针排序
• 三角化后计算三角形面积，其和即为交集面积$Area_{A \cap B}$
• $IOU_{AB} = \frac{Area_{A \cap B}}{Area_{A} + Area_{B} - Area_{A \cap B}}$

二、关键算子

2.1 坐标转换

以$(x, y, w, h, \theta)$表示矩形，在计算点集$P_{set}$时需要依据矩形四个顶点坐标，所以需要弄清楚中间转换过程。

如上图所示，红色框$A'B'C'D'$为目标斜框，绿色框$ABCD$表示轴向框，轴向框顺时针旋转$\theta$后得到目标斜框，现需要求出斜框各顶点$A', B', C', D'$的坐标。

步骤1：中心点到轴向框顶点向量

依据中心点$O'(x, y)$和框的宽度$w$和高度$h$可以得到中心点$O'$到轴向框各顶点坐标的向量分别为$O'A(\frac{w}{2}, \frac{h}{2}) \quad O'B(\frac{w}{2}, -\frac{h}{2})$, $O'C(-\frac{w}{2}, -\frac{h}{2}) \quad O'D(-\frac{w}{2}, \frac{h}{2})$

步骤2：向量顺时针旋转$\theta$

参考博客：平面向量旋转可知，顺时针旋转其旋转矩阵为

$$T = \begin{bmatrix} cos\theta & sin\theta \\ -sin\theta & cos\theta \\ \end{bmatrix}$$

所以向量$O'A' = T \cdot O'A, \quad O'B' = T \cdot O'B, \quad O'C' = T \cdot O'C, \quad O'D' = T \cdot O'D$
以$O'A'$求解为例，其横坐标$X_{O'A'} = cos\theta * \frac{w}{2} + sin\theta * \frac{h}{2}$, 纵坐标$Y_{O'A'} = -sin\theta * \frac{w}{2} + cos\theta * \frac{h}{2}$

所以

$O'A'(w * cos\theta * 0.5 + h * sin\theta * 0.5, -w * sin\theta * 0.5 + h * cos\theta * 0.5)$

因此：顶点$A'$的坐标为：

$A'(x + w * cos\theta * 0.5 + h * sin\theta * 0.5, y - w * sin\theta * 0.5 + h * cos\theta * 0.5)$

同理：

$O'B'(w * cos\theta * 0.5 - h * sin\theta * 0.5, -w * sin\theta * 0.5 - h * cos\theta * 0.5)$

$O'C'(-w * cos\theta * 0.5 - h * sin\theta * 0.5, w * sin\theta * 0.5 - h * cos\theta * 0.5)$

$O'D'(-w * cos\theta * 0.5 + h * sin\theta * 0.5, w * sin\theta * 0.5 + h * cos\theta * 0.5)$

所以有：

$B'(x + w * cos\theta * 0.5 - h * sin\theta * 0.5, y - w * sin\theta * 0.5 - h * cos\theta * 0.5)$

$C'(x - w * cos\theta * 0.5 - h * sin\theta * 0.5, y + w * sin\theta * 0.5 - h * cos\theta * 0.5) ==> C'(2x - X_{A'}, 2y - Y_{A'})$

$D'(x - w * cos\theta * 0.5 + h * sin\theta * 0.5, y + w * sin\theta * 0.5 + h * cos\theta * 0.5) ==> D'(2x - X_{B'}, 2y - Y_{B'})$

代码实现

struct RotatedBox {
  float x_ctr, y_ctr, w, h, a;
};

struct Point {
  float x, y;
  Point(const float& px = 0, const float& py = 0) : x(px), y(py) {}
  Point operator+(const Point& p) const {
    return Point(x + p.x, y + p.y);
  }
  Point& operator+=(const Point& p) {
    x += p.x;
    y += p.y;
    return *this;
  }
  Point operator-(const Point& p) const {
    return Point(x - p.x, y - p.y);
  }
  Point operator*(const float coeff) const {
    return Point(x * coeff, y * coeff);
  }
}

void GetRotatedVertices(const RotatedBox& box, Point(&pts)[4]) {
  // M_PI / 180. == 0.01745329251
  double theta = box.a * 0.01745329251;
  float cosTheta2 = (float)cos(theta) * 0.5f;
  float sinTheta2 = (float)sin(theta) * 0.5f;

  // y: top --> down; x: right --> left
  pts[0].x = box.x_ctr + sinTheta2 * box.h + cosTheta2 * box.w;
  pts[0].y = box.y_ctr + cosTheta2 * box.h - sinTheta2 * box.w;
  pts[1].x = box.x_ctr - sinTheta2 * box.h + cosTheta2 * box.w;
  pts[1].y = box.y_ctr - cosTheta2 * box.h - sinTheta2 * box.w;
  pts[2].x = 2 * box.x_ctr - pts[0].x;
  pts[2].y = 2 * box.y_ctr - pts[0].y;
  pts[3].x = 2 * box.x_ctr - pts[1].x;
  pts[3].y = 2 * box.y_ctr - pts[1].y;
}

2.2 线段求交

参考线段相交中方法一

代码实现

double EPS = 1e-5;
float Cross2d(const Point & A, const Point & B) {
  return A.x * B.y - B.x * A.y;
}

bool Insert(const Point& A, const Point& B, const Point& C, const Point&D, Point&P)
{
     
     Point AB = B - A;
     Point CD = D - C;
     float det = Cross2d(CD , AB);

      // This takes care of parallel lines
      if (std::fabs(det) <= 1e-14) {
        return false;
      }

      Point AC= C - A;

      double t = Cross2d(CD, AC) / det;
      double u = Cross2d(AB, AC) / det;

      if (t > -EPS && t < 1.0f + EPS && u > -EPS && u < 1.0f + EPS) {
         P = A + AB * t;
         return true;
      }
}

2.3 点是否在多边形内部

参考常见几何问题中第1个内容：点是否在多边形内部，可以采用其中射线法的思路。
但这里框是矩形，所以可以采用以下更简单的判别方法。

如上图所示，如果点$P$在矩形内部，则：
$\vec{AP}$ 到$\vec{AB}$的投影长度小于或等于$\vec{AB}$的长度且$\vec{AP}$ 到$\vec{AD}$的投影长度小于或等于$\vec{AD}$，
其中投影可以采用向量点乘计算

相反如果点$P$在矩形外部，则：
$\vec{AP}$ 到$\vec{AB}$的投影长度大于$\vec{AB}$的长度且$\vec{AP}$ 到$\vec{AD}$的投影长度大于$\vec{AD}$

代码实现

double EPS = 1e-5;
float Dot2d(const Point & A, const Point & B) {
  return A.x * B.x + A.y * B.y;
}

bool IsInner(const Point& A, const Point&B, const Point& C, const Point&D, const Point& P){
    const Point& AB = B - A;
    const Point& AD = D - A;
    float ABdotAB = Dot2d(AB, AB);
    float ADdotAD = Dot2d(AD, AD);

    Const Point& AP = P - A;
   
    float APdotAB = Dot2d(AP, AB);
    float APdotAD = Dot2d(AP, AD);

    if ((APdotAB > -EPS) && (APdotAD > -EPS) && (APdotAB < ABdotAB + EPS) && (APdotAD < ADdotAD + EPS)) {
        return true;
    }
    return false;
}

2.4 点集排序

由于矩形框相交形成的相交区域都是凸区域，所以可以借助凸包来完成逆时针排序。
参考博客凸包（Convex Hull）问题算法详解以及凸包算法（Graham扫描法）, 这里采用Graham(格拉翰)扫描法
博主给了个动图，很好的演示了算法流程, 动图地址请==>动图

算法步骤

1. 先找出y值最小的点，如果存在y值相等，则优先选择x值最小的作为起始点$P_{0}$，该点一定处于凸包上；
2. 以$P_{0}$作为原点，其他所有点减去$P_{o}$得到对应的向量；
   
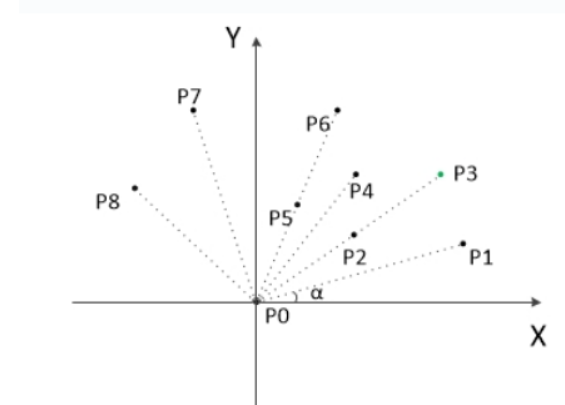
3. 计算所有向量与$X$轴正向的夹角$\alpha$，按从小到大进行排列，遇到$\alpha$相同的情况，则向量较短（即离$P_{0}$较近的点）的排在前面，得到初始点序$P_{1}, P_{2}, ..., P_{n}$，由几何关系可知点序中第一个点$P_{1}$和最后一个点$P_{n}$一定在凸包上；
4. 将$P_{0}$和$P_{1}$压入栈中，将后续点$P_{2}$作为当前点，跳转第8步；
5. 栈中最上面那个点形成向量$P_{ij}, i < j$， 利用叉乘判断当前点是否在该向量的左边还是右边或者向量上
6. 如果在左边或者向量上，则将当前点压入栈中，下一个点作为当前点，跳转第8步
7. 如果当前点在向量右边，则表明栈顶元素不在凸包上，将栈顶元素弹出，跳转第5步；
8. 判断当前点是否是最后一个元素，如果是则将其压缩栈中，栈中所有元素即是凸包上所有点，算法结束，否则跳到第5步。

代码实现

int ConvexHullGraham(const std::vector<Point> &p, std::vector<Point> &q, bool bShiftToZero = false) 
{
  const numIn = p.size();
  q.resize(numIn);
  
  // Step 1:
  // Find point with minimum y
  // if more than 1 points have the same minimum y,
  // pick the one with the minimum x.
  int t = 0;
  for (int i = 1; i < numIn; i++) {
    if (p[i].y < p[t].y || (p[i].y == p[t].y && p[i].x < p[t].x)) {
      t = i;
    }
  }
  Point& start = p[t]; // starting point

  // Step 2:
  // Subtract starting point from every points (for sorting in the next step)
  for (int i = 0; i < numIn; i++) {
    q[i] = p[i] - start;
  }

  // Swap the starting point to position 0
  Point tmp = q[0];
  q[0] = q[t];
  q[t] = tmp;

  // Step 3:
  // Sort point 1 ~ numIn according to their relative cross-product values
  // (essentially sorting according to angles)
  // If the angles are the same, sort according to their distance to origin
  float dist(numIn);
#if defined(__CUDACC__) || __HCC__ == 1 || __HIP__ == 1
  // compute distance to origin before sort, and sort them together with the
  // points
  for (int i = 0; i < numIn; i++) {
    dist[i] = Dot2d(q[i], q[i]);
  }

  // CUDA version
  // In the future, we can potentially use thrust
  // for sorting here to improve speed (though not guaranteed)
  for (int i = 1; i < numIn - 1; i++) {
    for (int j = i + 1; j < numIn; j++) {
      float crossProduct = Cross2d(q[i], q[j]);
      if ((crossProduct < -1e-6) || (std::fabs(crossProduct) < 1e-6 && dist[i] > dist[j])) {
        Point qTmp = q[i];
        q[i] = q[j];
        q[j] = qTmp;
        Point distTmp = dist[i];
        dist[i] = dist[j];
        dist[j] = distTmp;
      }
    }
  }
#else
  // CPU version
  std::sort(
      q + 1, q + numIn, [](const Point& A, const Point& B) -> bool {
        float temp = Cross2d(A, B);
        if (std::fabs(temp) < 1e-6) {
          return Dot2d(A, A) < Dot2d(B, B);
        } else {
          return temp > 0;
        }
      });
  // compute distance to origin after sort, since the points are now different.
  for (int i = 0; i < numIn; i++) {
    dist[i] = Dot2d(q[i], q[i]);
  }
#endif

  // Step 4:
  // Make sure there are at least 2 points (that don't overlap with each other)
  // in the stack
  int k; // index of the non-overlapped second point
  for (k = 1; k < numIn; k++) {
    if (dist[k] > 1e-8) {
      break;
    }
  }
  if (k == numIn) {
    // We reach the end, which means the convex hull is just one point
    q[0] = p[t];
    return 1;
  }
  q[1] = q[k];
  int m = 2; // 2 points in the stack
  // Step 5:
  // Finally we can start the scanning process.
  // When a non-convex relationship between the 3 points is found
  // (either concave shape or duplicated points),
  // we pop the previous point from the stack
  // until the 3-point relationship is convex again, or
  // until the stack only contains two points
  for (int i = k + 1; i < numIn; i++) {
    while (m > 1) {
      auto q1 = q[i] - q[m - 2], q2 = q[m - 1] - q[m - 2];
      // Cross2d() uses FMA and therefore computes round(round(q1.x*q2.y) -
      // q2.x*q1.y) So it may not return 0 even when q1==q2. Therefore we
      // compare round(q1.x*q2.y) and round(q2.x*q1.y) directly. (round means
      // round to nearest floating point).
      if (q1.x * q2.y >= q2.x * q1.y)
        m--;
      else
        break;
    }
    // Using double also helps, but float can solve the issue for now.
    // while (m > 1 && Cross2d(q[i] - q[m - 2], q[m - 1] - q[m - 2])
    // >= 0) {
    //     m--;
    // }
    q[m++] = q[i];
  }

  // Step 6 (Optional):
  // In general sense we need the original coordinates, so we
  // need to shift the points back (reverting Step 2)
  // But if we're only interested in getting the area/perimeter of the shape
  // We can simply return.
  if (!bShiftToZero) {
    for (int i = 0; i < m; i++) {
      q[i] += start;
    }
  }

  return m;
}

参考链接

Arbitrary-Oriented Scene Text Detection via Rotation Proposals
Rotated IoU 计算旋转矩形之间的重叠面积
Detector2