学习笔记——网络流

一、网络流的概念

网络流：所有弧上流量的集合$f = {f(u,v)}$，称为该流量网络的一个网络流。

定义：带权的有向图$G =(V,E) $，满足以下条件，则称为网络流图。：
1.有且仅有一个入度为0的顶点$ s $，称$s$为源点。
2.有且仅有一个出度为0的顶点$ t $，称$t$为汇点。
3.每条边的权值都为非负数，称为该边的容量，记作$c(u,v)$。

弧的流量：通过流量网络$G$中的每条弧$(u,v)$上的实际流量（简称流量），记作$f(u,v)$。

性质

对于任意一个时刻，设$f(u,v)$为实际流量，则整个图$G$的流网络满足3个性质：

$1$.流量限制：对于任意$u,v \in V $，$f(u,v) \le c(u,v)$。
$2$.反对称性：对于任意$u,v \in V $，$f(u,v) = -f(v,u)$，即从$u$到$v$的流量等于从$v$到$u$的流量的相反数。
$3$.流守恒性：对于任意$u \in V $，若$u$不为$S$或$T$，一定有$\sum f(u,v) = 0$，其中$(u,v) \in V $。简单来说就是流入$u$点的流量等于流出$u$点的流量，因为$u$点本身不会“制造”和“消耗”流量。

可行流：在流量网络$G$中满足以下条件的网络流$f$，称为可行流

$1$.弧流量限制条件:$0 \le f(u,v) \le c(u,v)$

$2$.平衡条件：流入$u$点的流量等于流出$u$点的流量（源点和汇点除外）

举个栗子：

上图中可行流为:$2+1+2=5$

零流：网络流上每条弧的流量都为$0$。

伪流：如果一个网络流只满足弧流量限制条件，不满足平衡条件，则这种网络流为伪流或容量可行流(预流推进算法有用)。

最大流最小割定理：在容量网络中，满足弧流量限制条件和平衡条件并且具有最大流量的可行流，称为网络最大流（简称最大流）。

最大流

对于网络流图$G$，流量最大的可行流$f$，称为最大流

弧的类型

$1$.饱和弧：$f(u,v)=c(u,v)$
$2$.非饱和弧：$f(u,v) < c(u,v)$
$3$.零弧：$f(u,v) = 0$
$4$.非零弧：$f(u,v) > 0$

链

在流量网络中，相邻两个顶点之间有一条弧（不要求所有弧的方向都和链的方向相同），则称该顶点序列($u_1$、$u_2$......$u_n$)为一条链。

割

无向图的割集：$C(A,B)$将图$G$分为$A$、$B$两个点集，$A$集和$B$集之间所有边的集合称为无向图的割集。

网络的割集：$C(S,T)$将网络$G$分为$S$、$T$两个点集（$s \in S$，$t \in T$，其中$s$为源点，$t$为汇点），$S$集和$T$集之间所有边的集合称为网络的割集。

带权图的割集：割集中所有边的权值和

通俗的理解一下: 割集好比是一个恐怖分子，把你家和自来水厂之间的水管网络砍断了一些，然后自来水厂无论怎么放水，水都只能从水管断口哗哗流走了，
你家就停水了，割的大小应该是恐怖分子应该关心的事，毕竟细管子好割一些，而最小割花的力气最小

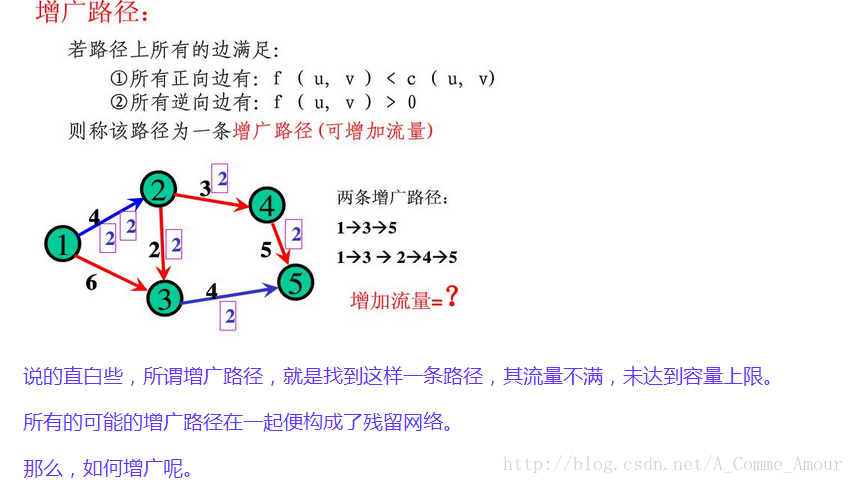
增广路

定义：如果一个可行流不是最大流，那么当前网络中一定存在一条增广路。

前置知识：

前向弧：方向和链的正方向一致的弧。

后向弧：方向和链的正方向一相反的弧。

设$f$是一个容量网络$G$中的一条可行流，$P$是从源点到汇点的一条链，若$P$满足：

$P$中所有前向弧都是非饱和弧

$P$中所有后向弧都是非零弧

则称$P$为关于可行流$f$的一条增广路，沿这增广路改进可行流的操作称为增广。

图文结合理解一下

残留容量

给定容量网络$G(V,E)$及可行流$f$，弧$(u,v)$上的残留容量记为$cl(u,v)=c(u,v)-f(u,v)$，每条弧上的残留容量表示这条弧上可以增加的流量。因为从顶点$u$到顶点$v$的流量减少，等价于从顶点$v$到顶点$u$的流量增加，所以每条弧$(u,v)$上还有一个反方向的残留容量$cl(v,u)=-f(u,v)$。

残余网络

在一个网络流图上，找到一条从源点到汇点的路径（即找到了一个流量）后，对路径上所有的边的容量都减去此次找到的量，并添加一条反向边（容量也等于此次找到的流量），这样得到的新图，就称为原图的“残余网络”。

费用流

最小费用最大流

最大流最小割定理:网络的最大流等于最小割

具体的证明分三部分

1.任意一个流都小于等于任意一个割。这个很好理解：自来水公司随便给你家通点水，构成一个流，恐怖分子随便砍几刀，砍出一个割，由于容量限制，每一根的被砍的水管子流出的水流量都小于管子的容量，每一根被砍的水管的水本来都要到你家的，现在流到外面，加起来得到的流量还是等于原来的流，
管子的容量加起来就是割，所以流小于等于割。由于上面的流和割都是任意构造的，所以任意一个流小于任意一个割

2.构造出一个流等于一个割。当达到最大流时，根据增广路定理，残留网络中$s$到$t$已经没有通路了，否则还能继续增广，我们把$s$能到的的点集设为$S$，不能到的点集为$T$，构造出一个割集$C[S,T]$，$S$到$T$的边必然满流，否则就能继续增广，这些满流边的流量和就是当前的流即最大流
把这些满流边作为割，就构造出了一个和最大流相等的割

3.最大流等于最小割。设相等的流和割分别为$Fm$和$Cm$，则因为任意一个流小于等于任意一个割，任意$F≤Fm=Cm≤$任意$C$。

证明如下：对于一个网络流图$G=(V,E)$，其中有源点$s$和汇点$t$，那么下面三个条件是等价的：

流$f$是图$G$的最大流

残留网络$Gf$不存在增广路

对于$G$的某一个割$(S,T)$，此时$f = C(S,T)$

首先证明$1 => 2$：
我们利用反证法，假设流$f$是图$G$的最大流，但是残留网络中还存在有增广路$p$，其流量为$fp$。则我们有流$ f' = f + fp > f $。这与$f$是最大流产生矛盾。

接着证明$2 => 3$：
假设残留网络$Gf$不存在增广路，所以在残留网络$Gf$中不存在路径从$s$到达$t$。我们定义$S$集合为：当前残留网络中$s$能够到达的点。同时定义$T=V-S$。此时$(S,T)$构成一个割$(S,T)$。且对于任意的$u∈S$,$v∈T$，有$f(u,v)=c(u,v)$。若$f(u,v) < c(u,v)$，则有$Gf(u,v) > 0$，$s$可以到达$v$，与$v$属于$T$矛盾。
因此有$f(S,T)=Σf(u,v)=Σc(u,v)=C(S,T)$。

最后证明$3 => 1$：
由于$f$的上界为最小割，当$f$到达割的容量时，显然就已经到达最大值，因此$f$为最大流。这样就说明了为什么找不到增广路时，所求得的一定是最大流。

以上概念均摘自A_Comme_Amour dalao的CSDN

二、网络流常用算法

一、最大流算法

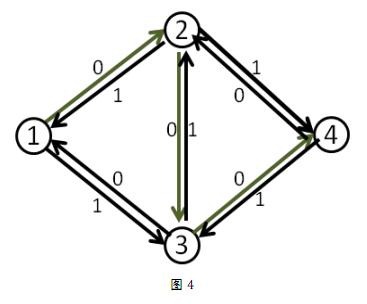
下面是所有最大流算法的精华部分：引入反向边

为什么要有反向边呢？

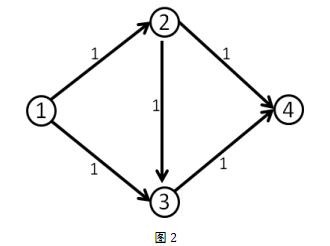
我们第一次找到了$1-2-3-4$这条增广路，这条路上的$delta$值显然是$1$。于是我们修改后得到了下面这个流。（图中的数字是容量）

这时候$(1,2)$和$(3,4)$边上的流量都等于容量了，我们再也找不到其他的增广路了，当前的流量是1。

但这个答案明显不是最大流，因为我们可以同时走$1-2-4$和$1-3-4$，这样可以得到流量为$2$的流。

那么我们刚刚的算法问题在哪里呢？问题就在于我们没有给程序一个“后悔”的机会，应该有一个不走$(2-3-4)$而改走$(2-4)$的机制。那么如何解决这个问题呢？回溯搜索吗？那么我们的效率就上升到指数级了。

而这个算法神奇的利用了一个叫做反向边的概念来解决这个问题。即每条边$(u,v)$都有一条反向边$(v,u)$，反向边也同样有它的容量。

我们直接来看它是如何解决的：

在第一次找到增广路之后，在把路上每一段的容量减少$delta$的同时，也把每一段上的反方向的容量增加$delta$。即在$dec(c[x,y],delta)$的同时，$inc(c[y,x],delta)$

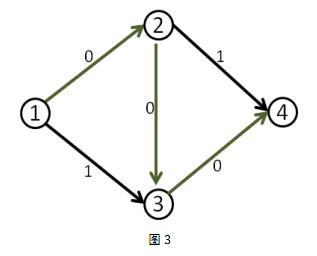
我们来看刚才的例子，在找到$1-2-3-4$这条增广路之后，把容量修改成如下

这时再找增广路的时候，就会找到$1-3-2-4$这条可增广量，即$delta$值为$1$的可增广路。将这条路增广之后，得到了最大流$2$。

那么，这么做为什么会是对的呢？我来通俗的解释一下吧。

事实上，当我们第二次的增广路走$3-2$这条反向边的时候，就相当于把$2-3$这条正向边已经是用了的流量给”退”了回去，不走$2-3$这条路，而改走从$2$点出发的其他的路也就是$2-4$。（有人问如果这里没有$2-4$怎么办，这时假如没有$2-4$这条路的话，最终这条增广路也不会存在，因为他根本不能走到汇点）同时本来在$3-4$上的流量由$1-3-4$这条路来“接管”。而最终$2-3$这条路正向流量$1$，反向流量$1$，等于没有流量。

这就是这个算法的精华部分，利用反向边，使程序有了一个后悔和改正的机会

(1)Edmonds-Karp算法

原理：求最大流的过程，就是不断找到一条源到汇的路径，若有，找出增广路径上每一段[容量-流量]（就是剩余流量）的最小值$delta$，然后构建残余网络，再在残余网络上寻找新的路径，使总流量增加。然后形成新的残余网络，再寻找新路径…..直到某个残余网络上找不到从源到汇的路径为止，最大流就算出来了。

思路：不断用BFS寻找增广路并不断更新最大流量值，直到网络上不存在增广路为止

实现过程：在$BFS$寻找一条增广路时，我们只需要考虑剩余流量不为$0$的边，然后找到一条从$S$到$T$的路径，同时计算出路径上各边剩余容量值的最小值$incf[n]$ ，则网络的最大流量就可以增加$incf[n]$（经过的正向边容量值全部减去$incf[n]$，反向边全部加上$incf[n]$）

$Q$：为什么不能用$dfs$找最大流

$A$：如果运气不好这种图会让程序执行$200$次$dfs$，虽然实际上最少只要$2$次我们就能得到最大流

时间复杂度：$O(nm^2)$

代码

const int N=2e2+10,M=5e3+10,INF=1<<29;
int n,m,s,t,ans;
int us[N][N];

int head[N],tot=1;
struct w_star{
	int nxt,to,wei;	
}e[M<<1];
il void add_e(int u,int v,int wei){
	e[++tot]=(w_star){head[u],v,wei};
	head[u]=tot;	
}

bool vis[N];
int incf[N],pre[N];
//incf[i]表示从源点到i节点的最小剩余流量

il bool bfs(){//找从源点到汇点的一条增广路
	memset(vis,0,sizeof(vis));
	queue <int> q;
	q.push(s);vis[s]=1;incf[s]=INF;pre[t]=-1;
	while(!q.empty()){
		int u=q.front();q.pop();
		for(R int i=head[u];i;i=e[i].nxt){
			if(e[i].wei){//剩余流量不为0的边
				int to=e[i].to;
				if(vis[to])	 continue;
				incf[to]=min(incf[u],e[i].wei);
                //传递最小剩余流量
				pre[to]=i;
                 //记录该边，方便修改边权 
				q.push(to);vis[to]=1;
			}
		}	
	}
	return pre[t]!=-1;
}

il void update(){
	int u=t;
	while(u!=s){
		int i=pre[u];
		e[i].wei-=incf[t];
        //正向边容量减去最小剩余流量
		e[i^1].wei+=incf[t];
        //反向边容量加上最小剩余流量（方便以后退流量）
		u=e[i^1].to;	
	}
	ans+=incf[t];//累加每一条增广路经的最小流量值 
}

signed main()
{
	n=read();m=read();s=read();t=read();
	for(R int i=1;i<=m;++i){
		int u=read(),v=read(),wei=read();
		if(!us[u][v]){//处理重边的操作
			add_e(u,v,wei);add_e(v,u,0);	
			us[u][v]=tot;
		}
		else e[us[u][v]^1].wei+=wei;
	}
	while(bfs()) update();//直到网络中不存在增广路 
	printf("%lld\n",ans);
	return 0;
}

(2)$Dinic$算法

$EK$算法每次都可能会遍历整个残量网络，但只找出一条增广路,是不是有点不划算？能不能一次找多条增广路呢？这时候，$Dinic$算法就闪亮登场了

思路：

每次多路增广：$u$ 点通过一条边，向 $v$ 输出流量以后，$v$ 会尝试到达汇点（到达汇点才真正增广），然后 $v$ 返回实际增广量。这时，如果 $u$ 还有没用完的供给，就继续尝试输出到其它边。

但是要警惕绕远路、甚至绕回的情况，不加管制的话极易发生。怎么管？

源点顺着残量网络想要到达其它点，需要经过一些边对吧？按照经过的边数（即源点出发以后的距离）把图分层，即用 bfs 分层。每次尝试给予时，只考虑给予自己下一层的点，就可以防止混乱。

综合上面两条。每回合也是从源点出发，先按照当前残量网络分一次层，随后多路增广，尽可能增加流量。增广过程中，会加入一些反向边，这些反向边逆着层次图，本回合并不会走。所以还需要进入下一回合。一直到 bfs 分层时搜不到汇点（即残量网络断了）为止。

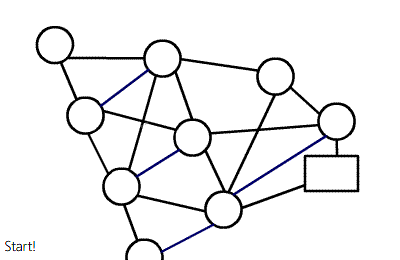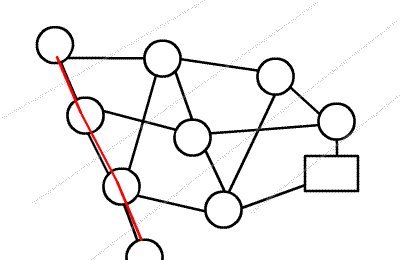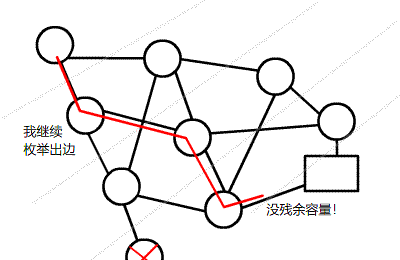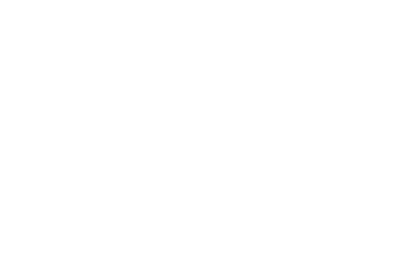
$Dinic$算法框架

1.在残量网络上$BFS$求出节点的层次，构造分层图

2.在分层图上$DFS$寻找增广路，在回溯时同时更新边权

时间复杂度：$O(n^2m)$


const int N=2e2+10,M=5e3+10,INF=1<<29;
int n,m,s,t,ans;

int head[N],tot=1;
struct w_star{
	int nxt,to,wei;	
}e[M<<1];
il void add_e(int u,int v,int wei){
	e[++tot]=(w_star){head[u],v,wei};
	head[u]=tot;	
}

int now[N],dep[N];
//now[i]记录当前走到的边的下一条边（当前弧优化）
//dep[i]记录i节点是在第几次bfs后找到的，即i节点在分成图的第几层

il bool bfs(){//在残量网络中构造分层图 
	for(R int i=1;i<=n;++i) dep[i]=INF;
   for(R int i=1;i<=n;++i) now[i]=head[i];//一开始没有走过任何一条边，所以记录s节点所连接的第一条边
   //实际上前两重循环应该从使用的最小下标到使用的最大下标
	queue <int> q;
	q.push(s);dep[s]=0;
	while(!q.empty()){
		int u=q.front();q.pop();
		for(R int i=head[u];i;i=e[i].nxt){
			int to=e[i].to;
			if(e[i].wei>0&&dep[to]==INF){//确保to节点有剩余流量且没有bfs被访问过
				q.push(to);
				dep[to]=dep[u]+1;//在分层图中的下一层
			}	
		}
	}	
	return dep[t]!=INF;
}	

il int dfs(int u,int sum){//sum是整条增广路对最大流的贡献
	if(u==t) return sum;
	int k,res=0;//k是当前最小的剩余容量
	for(R int i=now[u];i&&sum;i=e[i].nxt){
		now[u]=i;//当前弧优化 
		int to=e[i].to;
		if(e[i].wei>0&&(dep[to]==dep[u]+1)){
			k=dfs(to,min(sum,e[i].wei));
			if(k==0) dep[to]=INF;//剪枝，去掉增广完毕的点 
			e[i].wei-=k;
			e[i^1].wei+=k;
			res+=k;//res表示经过该点的所有流量和（相当于流出的总量） 
			sum-=k;//sum表示经过该点后剩余的流量，就是上文中u还有没用完的供给，就继续尝试输出到其它边
		}
	}
	return res;
}

signed main()
{
	n=read();m=read();s=read();t=read();
	for(R int i=1;i<=m;++i){
		int u=read(),v=read(),wei=read();
		add_e(u,v,wei);add_e(v,u,0);	
	}
	while(bfs()) ans+=dfs(s,INF);//流量守恒（流入=流出）
	printf("%lld\n",ans);
	return 0;
}

板子 (有动图的良心题解)(学习网络流的好题解)(我的代码)

(3)$HLPP$算法

$HLPP$ ($Highest$ $Label$ $Preflow$ $Push$)最高标签预流推进算法是处理网络最大流里两种常用方法——增广路&预流推进中，预流推进算法的一种。据传由$tarjan$发明~~怎么又是他~~ ，并被其他科学家证明了其复杂度是紧却的$O(n^2 \sqrt{m} )$ 。在随机数据中不逊色于普通的增广路算法，而在精心构造的数据中无法被卡，所以是一种可以替代$Dinic$的方法（随我怎么说，代码又长又难调，所以还是$Dinic$好啊$TAT$）

但无论怎样，$wiki$里面已经承认$HLPP$是现在最优秀的网络流算法了。

主要思路：对每个点记录超额流($Extra$ $Flow$) ，即允许流在非源点暂时存储，并伺机将超额流推送出去。不可推送的，就会流回源点。那么最终答案显然存储在 $Extra[T]$ 里面。（显然，因为$t$节点无法推送到其他节点，所以最终暂存在$t$节点的流量就是最大流量）

但同时这也有一个问题，就是会出现两个点相互推送不停的情况。为了防止这样，我们采用最高标号的策略：给每个点一个高度，对于一个点$u$以及它的伴点集合{$v$}，当且仅当$h_u = h_v + 1$时才可以推送流。并且我们对于源点$S$，设置$h_S = n$，并对于$S$实行无限制推送（源点流量无限）。那么最后的答案就保存在$Extra[T]$里面。

但有时，我们发现有个点是“谷”，即周围点的高度都比它高，但是它有超额流。那么我们此时考虑拔高它的高度，即重贴标签($relabel$)操作。

算法框架：

以下用$Extra_u$表示$u$的超额流，$h_u$表示$u$的高度，用$f_k$表示边$k$的容量。

倒着$BFS$一遍，搜出每个点离汇点的最短距离作为初始高度而不是把零作为初始高度（源点高度还是$n$）（$n$表示顶点的个数）

将$S$的流推送到每个与$S$相邻的点，同时把它们加入一个以高度为关键值排序的大根堆，保证之后每次取出的是高度最高且超额流不为$0$的点继续执行推送操作

对于点$u$的推送过程，若$Extra_u$减到了$0$，就立即退出（优化一）

对于每条出边$k$，推送的流量$F = min(f_k,Extra_u)$并执行$u,v$两个点的超额流增减操作。若$v$不在堆中，要把$v$放到堆里面。

若推送完毕后$Extra[u]$不为$0$，就从他的伴点集合里选一个高度最小的点（设为$h_{min}$），则新的$h_u = h_{min} + 1$，并把$u$入堆。

接下来我们发现，重贴标签的过程似乎与$ISAP$有点点像……所以我们不妨通过一个$Gap$数组来记录“断层情况”：即如果对于一个点$u$来说，他的伴点集{$v$}已经不存在$ h_u = h_v + 1$的点了，并且也不存在一个点$j$使得$h_j = h_u$那么这个地方就是一个断层($Gap$) ，那么也就是说，**对于所有$h_i > h_u$的点来说，它们把流推送到$h_u$的高度就不能继续推送了，所以我们直接$h_i = n + 1$，让他们回流到源点。**（优化二）

注意！这个写法是经典写法，其时间复杂度是紧却的$\Theta (n^2mlogn)$的

代码

const int N=2e4+10,M=4e5+10,INF=1<<29;
int n,m,s,t,ans;

int head[N],tot=1;
struct w_star{
	int nxt,to,wei;	
}e[M<<1];
il void add_e(int u,int v,int wei){
	e[++tot]=(w_star){head[u],v,wei};
	head[u]=tot;	
}

struct state{
	int num,h;
	il bool operator < (const state & now)const {
		return h<now.h;//以高度为关键字进行排序
	}
};
priority_queue <state> heap;
int h[N],gap[N],ext[N];
//h[i]记录节点i的高度
//gap[i]记录高度为i的节点的数量
//ext[i]记录节点i的超额流
bool vis[N];
int min_h;//记录伴生集合中高度最小的点

il void preflow_push(){
	int k;
	for(R int i=1;i<=n;++i)	 if(h[i]<INF) ++gap[h[i]];
	for(R int i=head[s];i;i=e[i].nxt){
		int to=e[i].to;
		if(k=e[i].wei){
			e[i].wei-=k;e[i^1].wei+=k;ext[s]-=k;ext[to]+=k;
			if(to!=t&&!vis[to]) {heap.push((state){to,h[to]});vis[to]=1;}
		}
	}
	while(!heap.empty()){
		int u=heap.top().num;heap.pop();min_h=INF;vis[u]=0;
		for(R int i=head[u];i;i=e[i].nxt){
			int to=e[i].to;
			if(e[i].wei&&h[u]==h[to]+1)	{
				int k=min(ext[u],e[i].wei);//找可以推进的最小流
				e[i].wei-=k;e[i^1].wei+=k;ext[u]-=k;ext[to]+=k;
				if(!vis[to]&&to!=s&&to!=t) {heap.push((state){to,h[to]});vis[to]=1;}
			}
			if(e[i].wei) min_h=min(min_h,h[to]);
			if(!ext[u]) break;//优化一
		}
		if(ext[u]){//出现断层，进行优化二
			if(!(--gap[h[u]]))	
				for(R int i=1;i<=n;++i) if(i!=s&&i!=t&&h[i]>h[u]&&h[i]<n+1) h[i]=n+1;
			h[u]=min_h+1;
			heap.push((state){u,h[u]});vis[u]=1;++gap[h[u]];
			
		}
	}
	
}

signed main()
{
	n=read();m=read();s=read();t=read();
	for(R int i=1;i<=m;++i) {
		int u=read(),v=read(),wei=read();
		add_e(u,v,wei);add_e(v,u,0);	
	}
	for(R int i=1;i<=n;++i) h[i]=INF;
	queue <int> q;
	q.push(t);h[t]=0;
	while(!q.empty()){//倒着BFS
		int u=q.front();q.pop();
		for(R int i=head[u];i;i=e[i].nxt){
			int to=e[i].to;
			if(h[to]>h[u]+1) h[to]=h[u]+1,q.push(to);
		}
	}
	if(h[s]==0) {cout<<0<<endl;return 0;}//源点就是汇点，则无解
	h[s]=n;preflow_push();printf("%lld\n",ext[t]);
	return 0;
}

板子 (理解算法用题解)(网络流算法大全题解)(代码+终极优化题解)(我的代码)

2.费用流算法

模型简述：给定一个流量网络，每一条边包含容量和单位费用两个属性，且这条边的费用相当于这条边的流量$\times $单位费用，求得到最大流时的最小费用。

SPFA算法

算法框架：

建立一个队列，将源点加入队列中，建立一个数组$cost$记录源点到所有点的最小费用（初始为$INF$，源点到本身的最小费用为$0$）。

从队列中取出队头元素，更新其连接的所有点的最小费用；如果更新成功且被更新点不在队列中，则把该点加入到队尾。

重复以上操作，直至队列为空或出现负权环

只要将$EK$算法中的$BFS$更改为$SPFA$即可。

$Q$：为什么不用效率更高的$Dinic$算法

$A$：因为$Dinic$算法一次找出多条增广路，不能保证一次增广的流量$\times $流到$t$点的最小费用就是该次增广的总费用（可能流最小费用的路径已经用过了（达到流量上限），但其他路径依然按最小费用进行计算，导致最小费用偏小）

代码（其实就是$EK$再套一个$SPFA$的板子）

const int N=5e3+10,M=5e4+10,INF=1<<30;
int n,m,s,t,max_flow,min_cost;
int head[N],tot=1;
struct w_star{
	int nxt,to,flow,cost;	
}e[M<<1];
il void add_e(int u,int v,int flow,int cost){
	e[++tot]=(w_star){head[u],v,flow,cost};
	head[u]=tot;
}	

bool vis[N];
int incf[N],cost[N],pre[N];

il bool SPFA(){
	for(R int i=1;i<=n;++i) vis[i]=0;
	for(R int i=1;i<=n;++i) cost[i]=INF;
	queue <int> q;
	q.push(s);vis[s]=1;incf[s]=INF;cost[s]=0;pre[t]=-1;
	while(!q.empty()){
		int u=q.front();q.pop();vis[u]=0;
		for(R int i=head[u];i;i=e[i].nxt){
			int to=e[i].to;
			if(e[i].flow&&cost[to]>cost[u]+e[i].cost){
				cost[to]=cost[u]+e[i].cost;
				pre[to]=i;
				incf[to]=min(incf[u],e[i].flow);	
				if(!vis[to]){q.push(to);vis[to]=1;}
			}
		}	
	}
	return pre[t]!=-1;
}

il void update(){
	int u=t;
	max_flow+=incf[t];min_cost+=incf[t]*cost[t];
	while(u!=s){
		int i=pre[u];
		e[i].flow-=incf[t];
		e[i^1].flow+=incf[t];
		u=e[i^1].to;
	}
}


signed main()
{
	n=read();m=read();s=read();t=read();
	for(R int i=1;i<=m;++i) {
		int u=read(),v=read(),flow=read(),cost=read();
		add_e(u,v,flow,cost);add_e(v,u,0,-cost);	
	}
	while(SPFA()) update();
	printf("%lld %lld",max_flow,min_cost);
	return 0;
}

板子 (网络流全模板题解)(代码用题解)(我的代码)

最小割算法

1.几个定义

1.割：给定一个图$G(V,E)$，其中$V$是点集，$E$是边集。在$E$中去掉一个边集$C$使得$G(V,E-C)$不连通，$C$就是图$G(V,E)$的一个割。

2.最小割：在$G(V,E)$所有割中，边权和最小的割就是最小割。

最大流最小割定理：

1.最小割等价于最大流。

2.最小割在最大流中一定是满流边，是增广路径中容量最小的边。

3.一条增广路径只对应一条最小割。（如果一条增广路中两条满流且都需要割掉，那一定通过反向边分成两条增广路）

一条最小割可以对应多条增广路径，但一条增广路径只能对应一条最小割（或最小割的可能性）

求最小割就是求增广路径中容量最小的边，所以恰好和最大流的求解一致。

1.板子题（建边方式神奇的题解（可以不用跑两次））（我的代码）

2.运用拆点的最小割（题解）（我的代码）

2.最大权闭合子图

首先有一个有向连通图，每个点带有一个权值，例如：

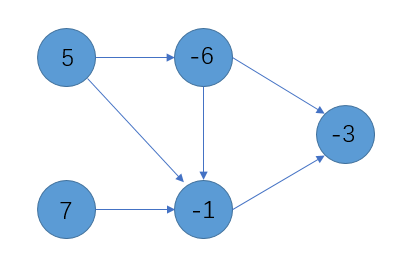
在此基础上构造一个超级源点$s$和超级汇点$t$，由$s$连向点权为正的点，容量为该点权值，由点权为负的点连向$t$，容量为该点权值的绝对值，原先点与点之间的边不变，容量为$INF$,如下图

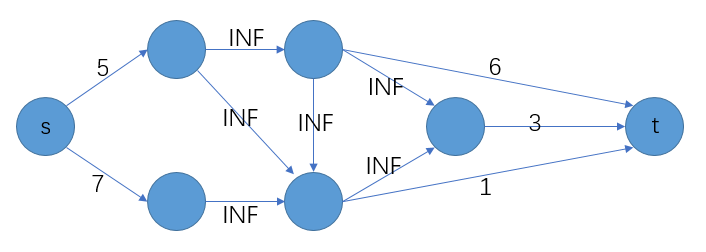
此时，我们可以得到以下结论：

$1$.该带权有向图的关于$s-t$的最小割是简单割。

简单割：割集中所有的边，都与$s$或$t$连接。

理解：该图中不与$s$或$t$相连的边容量都为$INF$，所以最小割一定在与$s$或$t$连接的边上。

$2$.该图中的每一个简单割会产生两个子图，我们设含有点$s$的图是图$S$，含有点$t$的图是图$T$，则图$S$是闭合图。

闭合图：取图中一些节点及与它们相连的边构成集合{$V$,$E$}，若集合$V$中任意节点连接的任意出弧所指向的终点也在集合$V$中 ，则{$V$,$E$}构成闭合图。

理解：简单割内不包含边权为$INF$的边，图$S$中没有边与图$T$连通，那么所有的权值不为$INF$的出弧都只能连接在图$S$之内，即为闭合图。

栗子：

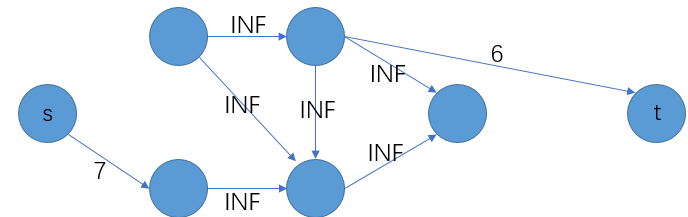
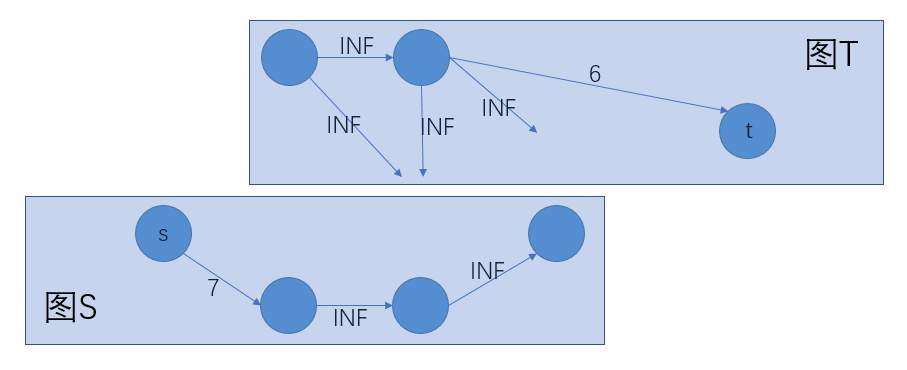
$3$.最小割产生的图S和图T，图S为最大权闭合子图

最大权闭合子图：在整个图中，有多个子图是满足闭合图的条件的，其中点权之和最大的，为最大权闭合子图。

理解：因为割集中的所有边不是连接在$s$上就是连接在$t$上，所以我们令割集中所有连接在$s$上的边的权值和为$x_1$,所有连接在$t$上的边的权值和为$x_2$，则割集中所有边的权值和为$X = x_1 + x_2$。

令图$S$中所有点的权值和为$W$，记其中正权值之和为$w_1$，负权值之和的绝对值为$-w_2$，$W = w_1 - w_2$。

所以$W + X = x_1 + x_2 + w_1 - w_2$

又因为$x_2 = w_2$（因为图$S$中所有负权值的点，必然连接到$t$点，而图$S$必然要与$t$分割开，所以割集中连接在$t$点上的边权值和就是图$S$中所有负权值点的权值之和）

所以$W + X = w_1 + x_1$

又因为$w_1 + x_1$为图中所有的正权值之和，记为$sum$，且$sum$为一个定值

所以$W = sum - X$，即“图$S$中所有点的正权值和”$=$“整个图中所有的正权值之和”$-$ “割集中所有的边权和”

所以只要减去最小割，就可以得到最大权闭合子图。

综上所述，我们可以得到求解此类题目的一般步骤：

1.记录整个图中所有的正权值和

2.建立对应的流网络，跑最大流（最大流在数值上等于最小割）

3.用正权值之和减去最大流，得到最大权闭合子图权值和。

最大权闭合子图

拓扑+最大权闭合子图板子（题解区（longlongzhu123大佬的题解））（我的代码）

板子题（题解）（我的代码）

原图中点的连边不为INF的最大权闭合子图（提供思路的题解）（我的代码（前向星数组一定要开大点！！！））

有思考的建边题（题解）（我的代码）

本题要求掌握顺难则反的思想，可以将题目转化为求不满足的要求的最小代价（最小割），并熟悉建边及退流思想

离散变量模型

立体图+有限制路径网络流（题解）（我的代码）

本题有路径限制，即最多可以流的节点数，就可以在临界点（设为$v$）连接一条回到初始点（设为$u$）的容量为$INF$边（保证不会被割掉），其中$u$到$v$之间跨过的点数就是限制。

平面图最短路

平面无向图（网络流题解）（我的代码（网络流））（对偶图最短路题解）（我的代码（对偶图最短路））

平面图最短路经典题（对偶图最短路题解）（我的代码）（标点方式新颖的代码）

对于平面图最短路，首先要了解其与最大流最小割的关系，有

对偶图最短路 $=$ 最大流 $=$ 最小割

一般来说，此类题目会卡最大流（包括当前弧优化的$Dinic$），所以一般要转化为对偶图最短路。主要了解对偶图的建边方式——对于每一个封闭区间看做一个点，分割相邻两个封闭区间的边的容量就是该两个封闭区间连边的长度，再由原先的起点和终点的连边将最外围的封闭区间分成两个点（即对偶图的起点和终点），用$dijkstra$跑一遍最短路即可。如下图：

新建点最小割

板子题（题解）（我的代码）

拆边为点求最小割（题解）（我的代码）

本题同样运用顺难则反的思想，求其不满足的最小代价。对于本题的边，可以从源点连接两条到该边两端点的边权为$(\dfrac{E_{a[i]}}{2})$的边，再连接两条从该边两端点到汇点的边权为$(\dfrac{E_{b[i]}}{2})$的边，因为有可能割的是一条连接源点的边，一条连接汇点的边，所以在这两点之间连接一条边权为$(\dfrac{E_{a[i]} + E_{b[i]}}{2}) + E_{c[i]}$的无向边，保证这种情况时该无向边被割掉或改为割与汇点相连的两条边，从而保证答案的正确性。

例题

1.输出路径的最大流问题 (题解)(我的代码)

2.基础建模题 (网络流24题题解)(我的代码)

3.输出路径的网络流基础题 ~~（别看他是紫，其实难度就是绿）~~ (题解)(我的代码)

4.最小路径覆盖问题 (题解)(我的代码)

本题主要要掌握拆点技巧，将一个点拆成两个（设为$x,y$），加一条由源点流向$x$和$y$流向汇点的边，将原图中要连边的两点（设为$u,v$）中$u_x$连向$v_y$，再跑一遍最大流，最大流量就是可以合并的边数，最小路径覆盖就是节点数减去最大流量。

5.建立分层图后跑网络流（其实只用$SPFA$就可以）(网络流题解)(我的代码)

输出路径的最大流基础题 (思路题解)(代码题解)(我的代码)

P2053 [SCOI2007]修车（拆点费用流（将M个师傅拆成N $\times$ M个，对应修第几次车））（题解）（我的代码）

P2050 [NOI2012] 美食节（题解）（题解）

本题是修车的加强版，由于可能会$T$飞，所以我们要优化：对于每一个厨师，只有当他做完一道菜后才有可能做其他的，所以我们一开始只要连该点乘一倍的情况，每次找到一条增广路后从所有菜向该节点连前一倍数加一的边，就可以大大减少$SPFA$的复杂度（~~防止我们SPFA~~）

P3980 [NOI2008] 志愿者招募（题解）（我的代码）

本题让我们对网络流有了更深的理解：在一些限制条件较多的题目中，我们可以用网络流来进行求解，又因为在本题中一个决策会导致多个限制条件的改变，而网络流的流量是一对一的，所以我们可以以一个人为一点流量，让这一点流量覆盖$s_i$到$t_i$天（具体就是从$s_i$天向$t_i+1$天连一条容量无限费用为$c_i$的边）。再以天数为点，相邻两天的边的容量为该天需要的人数的负数，补齐人数限制，跑一遍最小费用最大流即可。

注意到网络流的容量不能为负数，所以相邻两条边的容量为$INF-$当天的需要人数，费用为$0$。