浅谈网络最大流
网络最大流
目录
-
前言
-
双倍经验
-
网络流初步
-
网络最大流
-
\(EK\)增广路算法
-
\(Dinic\)算法
前言
这篇题解是当做学习记录写的,所以会对网络最大流这个概念进行讲解(\(dalao\)们可以忽略蒟蒻\(orz\))
双倍经验\(Time\)
-
洛谷P3376 【模板】 (\(Ek\)算法 / \(Dinic\)算法)
网络流初步
这里主要讨论一下网络流算法可能会涉及到的一些概念性问题
- 定义
对于任意一张有向图(也就是网络),其中有\(N\)个点、\(M\)条边以及源点\(S\)和汇点\(T\)
然后我们把\(c(x,y)\)称为边的容量
- 转换
为了通俗易懂,我们来结合生活实际理解上面网络的定义:
将有向图理解为我们城市的水网,有\(N\)户家庭、\(M\)条管道以及供水点\(S\)和汇合点\(T\)
是不是好理解一点?现在给出一张网络(图丑勿怪啊QAQ):
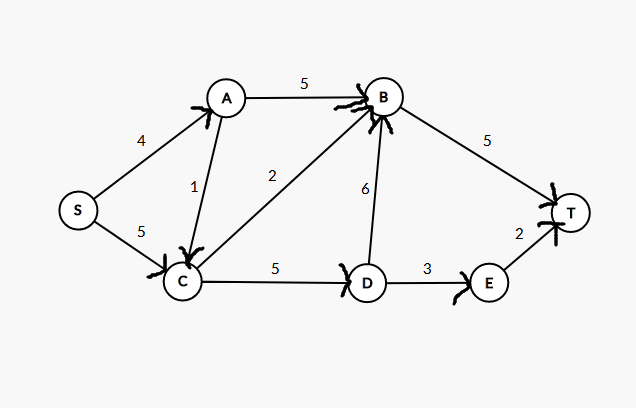
\(S->C->D->E->T\)就是该网络的一个流,\(2\)这个流的流量
- 流函数
和上面的\(c\)差不多,我们把\(f(x,y)\)称为边的流量,则\(f\)称为网络的流函数,它满足三个条件:
-
\(s(x,y)≤c(x,y)\)
-
\(f(x,y)=-f(y,x)\)
-
\(\forall\) \(x\)≠\(S\),\(x≠T\), \(\sum_{(u,x)∈E }f(u,x)=\sum_{(x,v)∈E }f(x,v)\)
这三个条件其实也是流函数的三大性质:
-
容量限制:每条边的流量总不可能大于该边的容量的(不然水管就爆了)
-
斜对称:正向边的流量=反向边的流量(反向边后面会具体讲)
-
流量守恒:正向的所有流量和=反向的所有流量和(就是总量始终不变)
- 残量网络
在任意时刻,网络中所有节点以及剩余容量大于\(0\)的边构成的子图被称为残量网络
最大流
对于上面的网络,合法的流函数有很多,其中使得整个网络流量之和最大的流函数称为网络的最大流,此时的流量和被称为网络的最大流量
最大流能解决许多实际问题,比如:一条完整运输道路(含多条管道)的一次最大运输流量,还有二分图(蒟蒻还没学二分图,学了之后会更新的qwq)
下面就来介绍计算最大流的两种算法:\(EK\)增广路算法和\(Dinic\)算法
\(Edmonds-Karp\)增广路算法
(为了简便,习惯称为\(EK\)算法)
- 首先来讲增广路是什么:
若一条从\(S\)到\(T\)的路径上所有边的剩余容量都大于0,则称这样的路径为一条增广路(剩余流量:\(c(x,y)-f(x,y)\))
- 然后就是\(EK\)算法的核心思想啦:
如上,显然我们可以让一股流沿着增广路从\(S\)流到\(T\),然后使网络的流量增大
\(EK\)算法的思想就是不断用BFS寻找增广路并不断更新最大流量值,直到网络上不存在增广路为止
- 再来讲理论实现过程:
在\(BFS\)寻找一条增广路时,我们只需要考虑剩余流量不为\(0\)的边,然后找到一条从\(S\)到\(T\)的路径,同时计算出路径上各边剩余容量值的最小值\(dis\),则网络的最大流量就可以增加\(dis\)(经过的正向边容量值全部减去\(dis\),反向边全部加上\(dis\))
- 反向边
插入讲解一下反向边这个概念,这是网络流中的一个重点
为什么要建反向边?
因为可能一条边可以被包含于多条增广路径,所以为了寻找所有的增广路经我们就要让这一条边有多次被选择的机会
而构建反向边则是这样一个机会,相当于给程序一个反悔的机会!
为什么是反悔?
因为我们在找到一个\(dis\)后,就会对每条边的容量进行减法操作,而直接更改值就会影响到之后寻找另外的增广路!
还不好理解?那我们举个通俗易懂的例子吧:
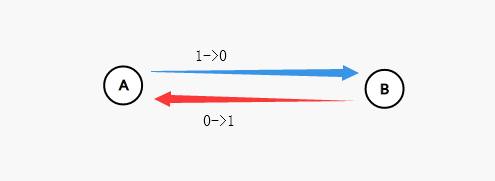
原本\(A\)到\(B\)的正边权是1、反边权是0,在第一次经过该边后(假设\(dis\)值为1),则正边权变为0,反边权变为1
当我们需要第二次经过该边时,我们就能够通过走反向边恢复这条边的原样(可能有点绕,大家好好理解一下)
以上都是我个人的理解,现在给出《算法竞赛进阶指南》上关于反向边的证明:
“当一条边的流量\(f(x,y)>0\)时,根据斜对称性质,它的反向边流量\(f(y,x)<0\),此时必定有\(f(y,x)<c(y,x)\),所以\(EK\)算法除了遍历原图的正向边以外还要考虑遍历每条反向边”
- 邻接表“成对存储”
我们将正向边和反向边存在“2和3”、“4和5”、“6和7”····
为什么?
因为在更新边权的时候,我们就可以直接使用\(xor 1\)的方式,找到对应的正向边和反向边(奇数异或1相当于-1,偶数异或1相当于+1)
代码实现如下(整个更新边权的操作函数):
inline void update() {
int x=t;
while(x!=s) {
int v=pre[x];
e[v].val-=dis[t];
e[v^1].val+=dis[t];
x=e[v^1].to;
}
ans+=dis[t];
}
- 适用范围
时间复杂度为\(O(nm^2)\),一般能处理\(10^3\)~\(10^4\)规模的网络
- 代码\(Code\)
(以本道模板题的代码为准,其他题可以将\(longlong\)换成\(int\)并且可以去掉处理重边操作)
#include <bits/stdc++.h>
using namespace std;
int n,m,s,t,u,v;
long long w,ans,dis[520010];
int tot=1,vis[520010],pre[520010],head[520010],flag[2510][2510];
struct node {
int to,net;
long long val;
} e[520010];
inline void add(int u,int v,long long w) {
e[++tot].to=v;
e[tot].val=w;
e[tot].net=head[u];
head[u]=tot;
e[++tot].to=u;
e[tot].val=0;
e[tot].net=head[v];
head[v]=tot;
}
inline int bfs() { //bfs寻找增广路
for(register int i=1;i<=n;i++) vis[i]=0;
queue<int> q;
q.push(s);
vis[s]=1;
dis[s]=2005020600;
while(!q.empty()) {
int x=q.front();
q.pop();
for(register int i=head[x];i;i=e[i].net) {
if(e[i].val==0) continue; //我们只关心剩余流量>0的边
int v=e[i].to;
if(vis[v]==1) continue; //这一条增广路没有访问过
dis[v]=min(dis[x],e[i].val);
pre[v]=i; //记录前驱,方便修改边权
q.push(v);
vis[v]=1;
if(v==t) return 1; //找到了一条增广路
}
}
return 0;
}
inline void update() { //更新所经过边的正向边权以及反向边权
int x=t;
while(x!=s) {
int v=pre[x];
e[v].val-=dis[t];
e[v^1].val+=dis[t];
x=e[v^1].to;
}
ans+=dis[t]; //累加每一条增广路经的最小流量值
}
int main() {
scanf("%d%d%d%d",&n,&m,&s,&t);
for(register int i=1;i<=m;i++) {
scanf("%d%d%lld",&u,&v,&w);
if(flag[u][v]==0) { //处理重边的操作(加上这个模板题就可以用Ek算法过了)
add(u,v,w);
flag[u][v]=tot;
}
else {
e[flag[u][v]-1].val+=w;
}
}
while(bfs()!=0) { //直到网络中不存在增广路
update();
}
printf("%lld",ans);
return 0;
}
\(Dinic\)算法
\(EK\)算法每次都可能会遍历整个残量网络,但只找出一条增广路
是不是有点不划算?能不能一次找多条增广路呢?
答案是可以的:\(Dinic\)算法
- 分层图&\(DFS\)
根据\(BFS\)宽度优先搜索,我们知道对于一个节点\(x\),我们用\(d[x]\)来表示它的层次,即\(S\)到\(x\)最少需要经过的边数。在残量网络中,满足\(d[y]=d[x]+1\)的边\((x,y)\)构成的子图被称为分层图(相信大家已经接触过了吧),而分层图很明显是一张有向无环图
为什么要建分层图?
讲这个原因之前, 我们还要知道一点:\(Dinic\)算法还需要\(DFS\)
现在再放上第一张图,我们来理解

根据层次的定义,我们可以得出:
第0层:S
第1层:A、C
第2层:B、D
第3层:E、T
在\(DFS\)中,从\(S\)开始,每次我们向下一层次随便找一个点,直到到达\(T\),然后再一层一层回溯回去,继续找这一层的另外的点再往下搜索
这样就满足了我们同时求出多条增广路的需求!
- \(Dinic\)算法框架
-
在残量网络上\(BFS\)求出节点的层次,构造分层图
-
在分层图上\(DFS\)寻找增广路,在回溯时同时更新边权
- 适用范围
时间复杂度:\(O(n^2m)\),一般能够处理\(10^4\)~\(10^5\)规模的网络
相较于\(EK\)算法,显然\(Dinic\)算法的效率更优也更快:虽然在稀疏图中区别不明显,但在稠密图中\(Dinic\)的优势便凸显出来了(所以\(Dinic\)算法用的更多)
此外,\(Dinic\)算法求解二分图最大匹配的时间复杂度为\(O(m\sqrt{n})\)
- 代码\(Code\)
这份代码是本模板题的AC代码,但是使用到了\(Dinic\)算法的两个优化:当前弧优化+剪枝
#include <bits/stdc++.h>
using namespace std;
const long long inf=2005020600;
int n,m,s,t,u,v;
long long w,ans,dis[520010];
int tot=1,now[520010],head[520010];
struct node {
int to,net;
long long val;
} e[520010];
inline void add(int u,int v,long long w) {
e[++tot].to=v;
e[tot].val=w;
e[tot].net=head[u];
head[u]=tot;
e[++tot].to=u;
e[tot].val=0;
e[tot].net=head[v];
head[v]=tot;
}
inline int bfs() { //在惨量网络中构造分层图
for(register int i=1;i<=n;i++) dis[i]=inf;
queue<int> q;
q.push(s);
dis[s]=0;
now[s]=head[s];
while(!q.empty()) {
int x=q.front();
q.pop();
for(register int i=head[x];i;i=e[i].net) {
int v=e[i].to;
if(e[i].val>0&&dis[v]==inf) {
q.push(v);
now[v]=head[v];
dis[v]=dis[x]+1;
if(v==t) return 1;
}
}
}
return 0;
}
inline int dfs(int x,long long sum) { //sum是整条增广路对最大流的贡献
if(x==t) return sum;
long long k,res=0; //k是当前最小的剩余容量
for(register int i=now[x];i&∑i=e[i].net) {
now[x]=i; //当前弧优化
int v=e[i].to;
if(e[i].val>0&&(dis[v]==dis[x]+1)) {
k=dfs(v,min(sum,e[i].val));
if(k==0) dis[v]=inf; //剪枝,去掉增广完毕的点
e[i].val-=k;
e[i^1].val+=k;
res+=k; //res表示经过该点的所有流量和(相当于流出的总量)
sum-=k; //sum表示经过该点的剩余流量
}
}
return res;
}
int main() {
scanf("%d%d%d%d",&n,&m,&s,&t);
for(register int i=1;i<=m;i++) {
scanf("%d%d%lld",&u,&v,&w);
add(u,v,w);
}
while(bfs()) {
ans+=dfs(s,inf); //流量守恒(流入=流出)
}
printf("%lld",ans);
return 0;
}
- 当前弧优化
对于一个节点\(x\),当它在\(DFS\)中走到了第\(i\)条弧时,前\(i-1\)条弧到汇点的流一定已经被流满而没有可行的路线了
那么当下一次再访问\(x\)节点时,前\(i-1\)条弧就没有任何意义了
所以我们可以在每次枚举节点\(x\)所连的弧时,改变枚举的起点,这样就可以删除起点以前的所有弧,来达到优化剪枝的效果
对应到代码中,就是\(now\)数组
后序
终于写完了....现在来特别感谢一些:@那一条变阻器 对于使用\(EK\)算法过掉本题的帮助 以及 @取什么名字 讲解\(Dinic\)算法的\(DFS\)部分内容
如果本篇题解有任何错误或您有任何不懂的地方,欢迎留言区评论,我会及时回复、更正,谢谢大家orz!


 浙公网安备 33010602011771号
浙公网安备 33010602011771号