采用pso进行pid参数寻优

粒子群优化（PSO）算法用于PID参数寻优是一种有效的优化方法

粒子群优化（PSO）算法原理

PSO算法是一种基于群体智能的优化算法，灵感来源于鸟群或鱼群的觅食行为。PSO通过在多维搜索空间中移动一组“粒子”（代表潜在解）来找到最优解。每个粒子都有自己的位置和速度，并逐步向最佳解靠近。PSO算法具有全局搜索能力和较高的计算效率，常用于求解复杂的优化问题。

基于PSO的PID参数整定方法

在基于PSO的PID参数整定中，将PID控制器的参数（比例增益Kp、积分增益Ki和微分增益Kd）编码为粒子的位置向量。目标函数通常与控制系统的性能指标相关，如误差积分（IAE）、时间乘以误差绝对值积分（ITAE）等。优化目标是最小化这个性能指标。

具体步骤如下：

1. 初始化粒子群：包括粒子的位置（PID参数）、速度和适应度值。粒子的位置和速度在搜索空间中随机初始化。
2. 评估适应度值：使用当前PID参数对控制系统进行仿真，并计算性能指标。
3. 更新个体历史最优位置（pBest）和全局最优位置（gBest）：每个粒子记录自己目前遇到的最佳位置，所有粒子中适应度值最优的粒子位置为全局最优位置。
4. 更新粒子速度和位置：根据公式更新粒子速度和位置，使粒子逐渐靠近最优解。
5. 重复步骤2-4：直到满足终止条件（如达到最大迭代次数或性能指标足够好）。
6. 输出全局最优位置：作为整定后的PID参数。

参数编码与解码方式

在PSO算法中，每个粒子的位置代表了潜在的解决方案，即PID参数的可能值。参数编码是将PID参数组合转化为粒子位置的过程，而解码则是将粒子位置还原为PID参数值的过程。编码策略可以简单地将P、I、D值线性映射到粒子的位置坐标上。

粒子的运动与信息更新规则

粒子的运动由其自身的历史最优位置（pbest）和群体的历史最优位置（gbest）引导。粒子在每一步更新时，会根据当前位置、速度以及pbest和gbest来进行速度和位置的更新。速度更新公式为：

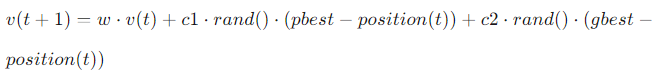
其中，( w ) 是惯性权重，( c1 ) 和 ( c2 ) 是学习因子，( rand() ) 是介于0和1之间的随机数。

终止条件与性能评估

终止条件是PSO算法停止搜索的条件，常见的终止条件包括达到最大迭代次数、连续迭代后适应度值改进小于某个阈值或者系统达到预设的性能标准。性能评估是通过运行仿真或实际控制系统来检验找到的PID参数是否满足系统性能要求。

实验结果与分析

通过MATLAB仿真，展示了基于PSO的PID参数整定方法的优越性。仿真结果表明，该方法能够自动调整PID控制器的参数，使控制系统的性能达到最优。与传统的PID参数整定方法相比，该方法具有更高的效率和准确性。

总结来说，PSO算法在PID参数优化中，通过模拟自然界的群体行为，能够高效搜索参数空间，找到满足控制性能指标的最优PID参数组合。然而，参数的选择和适应度函数的设计对算法的性能有着显著的影响。

参考代码 PSO算法优化PID参数