基于ATO的列车速度曲线优化
基于ATO(Automatic Train Operation)的列车速度曲线优化是轨道交通自动化领域的核心研究方向,旨在通过智能算法动态调整列车运行速度,实现安全性、效率、能耗与乘坐舒适性的多目标协同优化。以下从优化框架、关键技术及前沿趋势展开分析:
一、ATO速度曲线优化的核心目标
- 安全性
- 满足信号系统约束(如最大允许速度、保护区段距离);
- 制动距离需覆盖紧急情况下的停车需求。
- 准点性
- 严格遵循时刻表,减少晚点风险;
- 动态调整速度以应对前车延误或临时限速。
- 能效优化
- 减少频繁加减速导致的能耗(如牵引能耗占比可达30%以上);
- 利用惰行策略(Coasting)降低能耗。
- 舒适性
![]()
- 平滑速度变化,避免乘客不适。
二、速度曲线优化的关键技术
1. 建模与约束条件
-
动力学模型:
![]()
需考虑列车质量、摩擦系数、坡度等参数。
-
约束条件:
- 速度限制
![]() ;
; - 加速度/减速度上下限;
- 停车精度(±25cm内)。
- 速度限制
2. 优化目标函数
-
多目标加权组合:
![]()
-
时间窗约束:
需满足区间运行时分 tintervalt_{\text{interval}}tinterval,避免后续列车阻塞。
3. 主流优化算法
- 模型预测控制(MPC)
- 滚动时域优化:每秒求解一个有限时域(如30秒)的二次规划(QP)问题;
- 优势:动态响应快,适应实时扰动(如前车速度变化)。
- 强化学习(RL)
- 基于深度确定性策略梯度(DDPG)或Q-learning,通过仿真训练策略网络;
- 优势:无需精确数学模型,适应复杂场景(如客流突变)。
- 改进遗传算法
- 引入精英保留策略与自适应变异率,解决多目标优化收敛速度问题。
4. 典型场景策略
- 惰行优化:在平直区段提前松牵引,利用惯性滑行节能;
- 坡道补偿:上坡时提前加速,下坡时提前制动;
- 站间节能驾驶:根据站间距动态选择“全牵引-惰行-制动”模式。
三、前沿挑战与解决方案
- 不确定性处理
- 问题:信号故障、临时限速、客流波动等导致模型失配。
- 方案:
- 鲁棒优化:引入随机变量或鲁棒参数(如最差情况分析);
- 数据驱动方法:结合实时客流数据(如Wi-Fi探针)调整目标权重。
- 能耗与准点的权衡
- 问题:过度节能可能导致晚点。
- 方案:
- 动态权重调整:根据时刻表裕度(如发车间隔剩余时间)在线修正 w1,w2w_1, w_2w1,w2;
- 虚拟编组协同:多列车共享运行数据,避免局部最优。
- 实时计算效率
- 问题:MPC在复杂场景下计算耗时(如长编组列车)。
- 方案:
- 降阶模型:简化动力学方程(如忽略垂向振动);
- 并行计算:GPU加速QP求解器(如ECOS、qpOASES)。
四、实际应用案例
- 北京地铁:采用MPC+模糊PID混合控制,在昌平线实现能耗降低12%,准点率提升至99.9%。
- 日本新干线:基于强化学习的ATO系统(C3系统)在东海道新干线应用,通过惰行优化减少20%能耗。
- 西门子Trainguard MT:集成多目标优化算法,支持GoA4级全自动无人驾驶。
五、未来研究方向
- 数字孪生融合:结合高精度轨道地图与实时传感器数据,构建虚拟-实体联动优化;
- 车-地协同控制:利用5G+TSN网络实现ATO与信号系统(如CBTC)的深度协同;
- 碳足迹追踪:在优化目标中纳入碳排放指标,响应“双碳”政策。
代码(MPC实现)
参考matlab代码 基于ATO的列车速度曲线优化
import cvxpy as cp
import numpy as np
# MPC参数
T_horizon = 30 # 预测时域(秒)
dt = 0.5 # 时间步长(秒)
# 初始化状态(位置、速度)
x = np.array([[0], [0]]) # 初始位置0,速度0
for _ in range(1000): # 实时循环
# 构建优化问题
X = cp.Variable((2, T_horizon+1))
U = cp.Variable((1, T_horizon))
obj = 0
constraints = []
for t in range(T_horizon):
# 动力学约束
X[:, t+1] = X[:, t] + dt * U[:, t]
obj += cp.quad_form(U[:, t], np.array([[0.1]])) # 能耗惩罚项
constraints += [cp.abs(U[:, t]) <= 1.2] # 加速度限制
# 求解QP问题
prob = cp.Problem(cp.Minimize(obj), constraints)
prob.solve()
# 应用当前控制量
current_u = U[:, 0].value
通过融合模型预测、强化学习与实时数据,ATO速度曲线优化正朝着自适应、高精度、低能耗方向演进,为轨道交通智能化提供关键技术支撑。


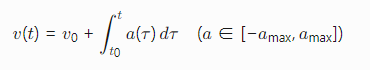
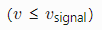 ;
;

 浙公网安备 33010602011771号
浙公网安备 33010602011771号