浅谈高斯消元

线性代数相关定义

线型方程组

设有 \(n\) 个未知数 \(m\) 个方程的线性方程组

\[\begin{cases} a_{11}x_1 + a_{12}x_2 + \dots + a_{1n}x_n = b_1\\ a_{21}x_1 + a_{22}x_2 + \dots + a_{2n}x_n = b_2\\ \dots\text{}\dots\text{}\dots\text{}\dots\\ a_{m1}x_1 + a_{m2}x_2 + \dots + a_{mn}x_x = b_m \end{cases} \]

其中 \(a_{ij}\) 为第 \(i\) 个方程第 \(j\) 个未知数的系数，\(b_i\) 是第 \(i\) 个方程的常数项。
当常数项 \(b_1,b_2,b_3,\dots,b_m\) 不全为零时，该线性方程组叫做 \(n\) 元非齐次线性方程组。
当 \(b_1,b_2,b_3,\dots,b_m\) 全为零时，该线性方程组

\[\begin{cases} a_{11}x_1 + a_{12}x_2 + \dots + a_{1n}x_n = 0\\ a_{21}x_1 + a_{22}x_2 + \dots + a_{2n}x_n = 0\\ \dots\text{}\dots\text{}\dots\text{}\dots\\ a_{m1}x_1 + a_{m2}x_2 + \dots + a_{mn}x_x = 0 \end{cases} \]

称为 \(n\) 元齐次线性方程组。

\(n\) 元线性方程组往往简称为线性方程组或方程组。

对于 \(n\) 元齐次线性方程组，\(x_1 = x_2 = x_3 = x_n = 0\) 一定是它的解，这个解叫齐次线性方程组的零解。如果有一组不全为零的数是它的解，则叫做齐次线性方程组的非零解。

齐次线性方程组一定有零解，不一定有非零解。

矩阵

对于非齐次线性方程组

\[\begin{cases} a_{11}x_1 + a_{12}x_2 + \dots + a_{1n}x_n = b_1\\ a_{21}x_1 + a_{22}x_2 + \dots + a_{2n}x_n = b_2\\ \dots\text{}\dots\text{}\dots\text{}\dots\\ a_{m1}x_1 + a_{m2}x_2 + \dots + a_{mn}x_x = b_m \end{cases} \]

有如下几个矩阵：

\[A = \begin{pmatrix} a_{ij} \end{pmatrix} ,x = \begin{pmatrix}x_1\\x_2\\ \vdots \\x_n\end{pmatrix},b =\begin{pmatrix} b_1\\b_2\\ \vdots \\ b_m\end{pmatrix},B = \begin{pmatrix} a_{11}&a_{12}&\dots &a_{1n}&b_1\\ a_{21}&a_{22}&\dots &a_{2n}&b_2 \\ \vdots & \vdots & &\vdots &\vdots\\ a_{m1}&a_{m2}& \dots & a_{mn} & b_m \end{pmatrix}, \]

其中 \(A\) 成为系数矩阵，\(x\) 称为未知数矩阵，\(b\) 称为常数项矩阵，\(B\) 称为增广矩阵。高斯消元就是在增广矩阵上进行的。

矩阵的初等变换

下面三种变换称为矩阵的初等行变换：

  1. 对换两行（对换 \(i,j\) 两行，记作 \(r_i \leftrightarrow r_j\)）
  2. 以非零数 \(k\) 乘上某一行中所有元（第 \(i\) 行乘以 \(k\)，记作 \(r_i \times k\)）
  3. 把某一行数所有元的 \(k\) 倍加到另一行的所有元上去（第 \(j\) 行的 \(k\) 倍加到第 \(i\) 行上，记作 \(r_i+k\times r_j\)）

把矩阵的初等行变换的“行”换成“列”，就得到了矩阵的初等列变换。
矩阵的初等行变换和矩阵的初等列变换，统称为初等变换。

高斯消元

主要思想

反复运用初等变换将原矩阵变换为形如

\[\begin{pmatrix} 1&a_{12} &a_{13} & \dots & a_{1n} &b_1 \\ &1&a_{23}&\dots&a_{2n}&b_2\\ &&\vdots&\vdots&\vdots&\vdots\\&&&&1&b_n \end{pmatrix} \]

的上三角矩阵，然后从下至上回带求解。
而且可以观察到每一行对应主元之下，该主元的系数都为 \(0\)。

主要步骤

  • 找到当前主元系数不为 \(0\) 的一行（这里通常也找系数绝对值较大的一行）。
  • 将这一行与当前处理到的行交换。
  • 运用初等变换将主元的系数变为 \(1\)。
  • 运用初等变换将其余行（不包含当前行上面的行）的主元的系数变为 \(0\)（目的是变成上三角矩阵）。

最后通过上三角矩阵回带求解，得到答案。

无解 & 无穷解

通过初中知识可知，\(n\) 个未知数要有 \(n\) 个方程才能求解，如果在找主元不为 \(0\) 的一行是找不到了（即这个主元的所有系数都为 \(0\)），这是肯定是会出现两种情况。

  1. 无解，出现 \(0 = k \not= 0\) 时。
  2. 无穷解，出现 \(0 = 0\) 时。

故处理时如果出现找不到主元时先跳过这一行，最后在所有系数都为 \(0\) 的行中判断常数即可。

无解举例

\[\begin{cases} 3x_1 + 7x_2 - 5x_3 = 47\\ x_1 + 4x_2 + x_3 = 58\\ 2x_1 + 3x_2 - 6x_3 = 5 \end{cases} \Rightarrow \begin{pmatrix} 3&7&-5&47\\1&4&1&58\\2&3&-6&5 \end{pmatrix} \Rightarrow \begin{pmatrix} 3&7&-5&47\\0&5&8&127\\0&0&0&16 \end{pmatrix} \]

此时无解。

无穷解举例

\[\begin{cases} 3x_1 + 7x_2 - 5x_3 = 47\\ x_1 + 4x_2 + x_3 = 58\\ 2x_1 + 3x_2 - 6x_3 = -11 \end{cases} \Rightarrow \begin{pmatrix} 3&7&-5&47\\1&4&1&58\\2&3&-6&-11 \end{pmatrix} \Rightarrow \begin{pmatrix} 3&7&-5&47\\0&5&8&127\\0&0&0&0 \end{pmatrix} \]

此时有无数解。

解释

下面通过几组样例，在程序中插入 printf 语句，追踪一下高斯消元的执行过程。

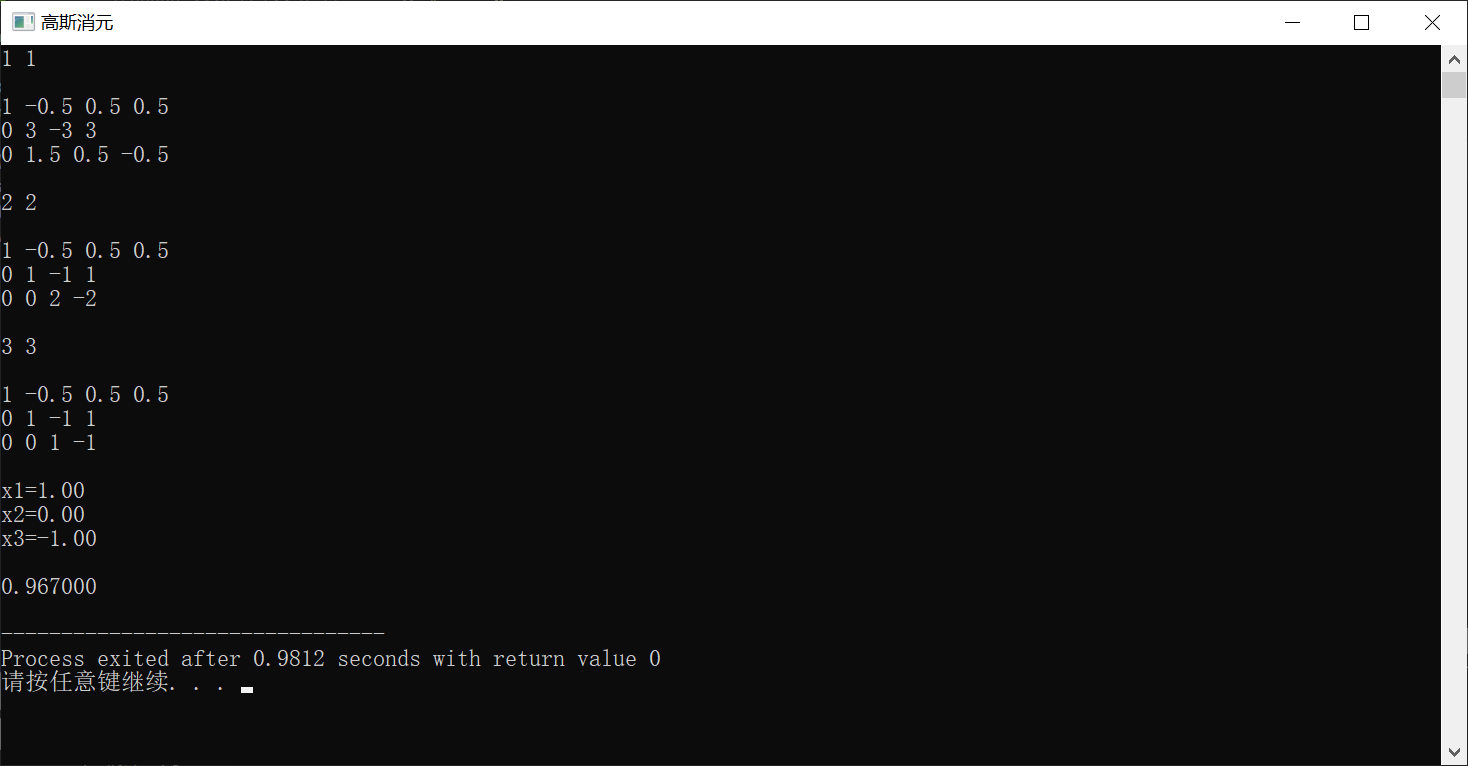
唯一解

输入：

3
2 -1 1 1
4 1 -1 5
1 1 1 0

输出：

x1=1.00
x2=0.00
x3=-1.00

唯一解

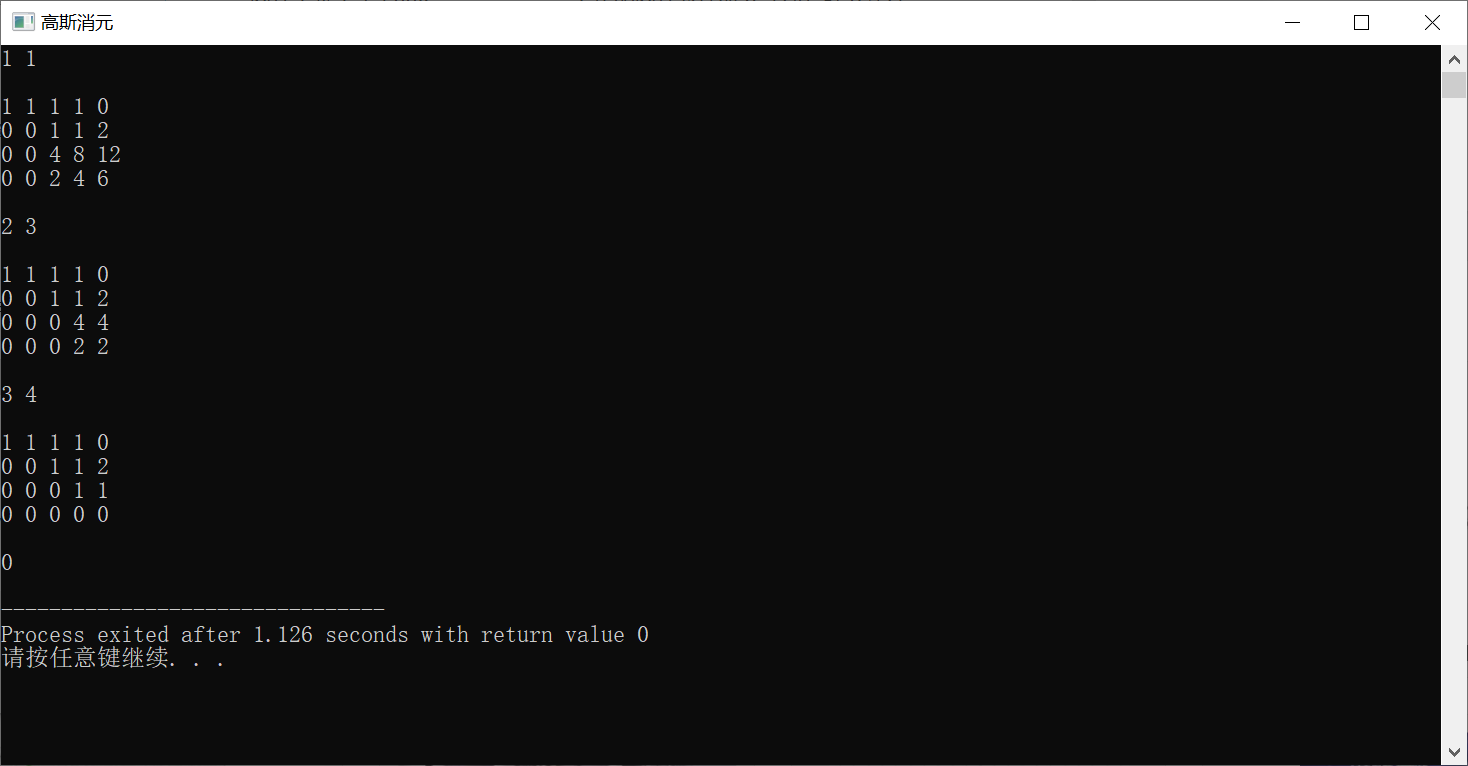
无穷解
输入：

4
0 0 2 4 6
0 0 1 1 2
0 0 4 8 12
1 1 1 1 0

输出：

0

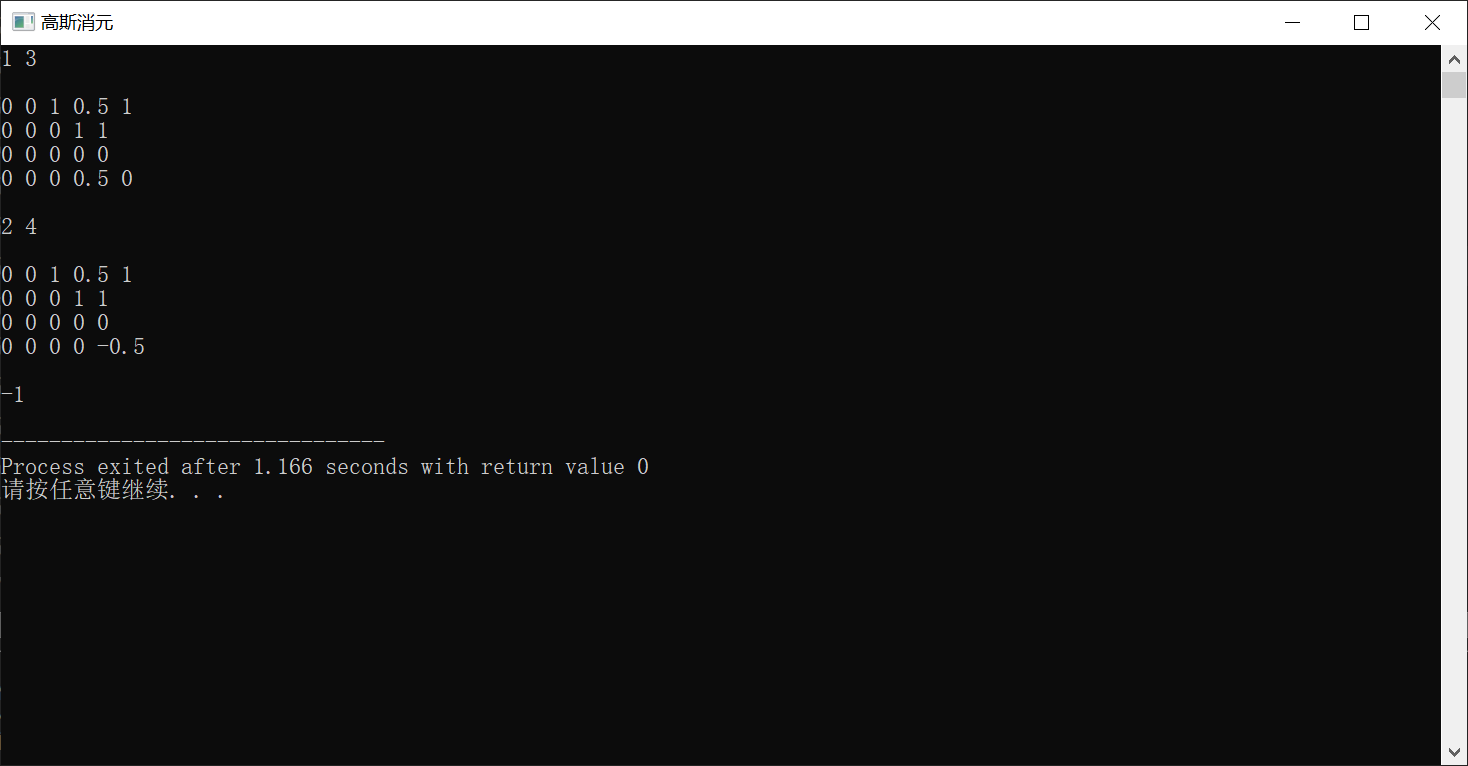
无解
输入：

4
0 0 2 1 2
0 0 1 1 1
0 0 0 1 1
0 0 0 0 0

输出：

-1

无解

代码实现

模板题：
P2455 [SDOI2006] 线性方程组

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
#include <ctime>

using namespace std;

const int maxn = 105;
const double eps = 1e-7;//精度
double a[maxn][maxn];
double ans[maxn];
int n;

void print()
{
	puts("");
	for (int i = 1; i <= n; i++)
	{
		for (int j = 1; j <= n + 1; j++) cout << a[i][j] << " ";
		puts("");
	}
	puts("");
}//调试，输出矩阵

void gauss()
{
	//row 行 col 列
	int col = 1, row = 1;
	for (col = 1; col <= n; col++)//枚举主元所在列（1~n）
	{
		//step1 找到主元非0的一行
		int t = row;
		for (int i = row; i <= n; i++)
		{
			if (fabs(a[i][col]) > eps)
			{
				t = i;
				break;
			}
		}
		// step2
		if (fabs(a[t][col]) < eps) continue;//主元系数为0，即产生了自由元，先暂且不管
		swap(a[row], a[t]);//否则替换两行

		//step3 将主元系数置1，注意枚举顺序
		for (int i = n + 1; i >= row; i--)
		{
			a[row][i] /= a[row][col];
		}

		//step4 将下面所有的主元系数消为0
		for (int i = row + 1; i <= n; i++)
		{
			for (int j = n + 1; j >= col; j--)
			{
				a[i][j] -= a[i][col] * a[row][j];
			}
		}

		//step5 处理下一个主元
		row++;
	}

	//处理的主元个数小于n，产生了自由元，一定是无解/无穷解
	if (row <= n)
	{
		for (int i = row; i <= n; i++)
		{
			if (fabs(a[i][n + 1]) > eps)
			{
				cout << "-1" << endl;
				exit(0);
			}
		}
		puts("0");
		exit(0);
		return;
	}
	else
	{
		//step6 回代求解答案
		for (int i = n; i >= 1; i--)
		{
			ans[i] = a[i][n + 1];
			for (int j = i + 1; j <= n; j++)
			{
				ans[i] -= ans[j] * a[i][j];
			}
		}
		for (int i = 1; i <= n; i++) printf("x%d=%.2lf\n", i, ans[i]);
	}
}




int main()
{
#ifndef ONLINE_JUDGE
#define LOCAL
	//freopen("in.txt","r",stdin);
#endif
	cin >> n;
	for (int i = 1; i <= n; i++)
	{
		for (int j = 1; j <= n + 1; j++)
		{
			scanf("%lf", &a[i][j]);
		}
	}
	gauss();
#ifdef LOCAL
	fprintf(stderr, "%f\n", 1.0 * clock() / CLOCKS_PER_SEC);
#endif
	return 0;
}

高斯-约当消元法

主要思想

与高斯消元思想相近，但略有不同。
反复运用初等变换将系数矩阵变换为形如

\[\begin{pmatrix} 1&0&0&\dots&0\\ 0 & 1 &0 & \dots &0\\ \vdots & \vdots & \vdots & &\vdots\\ 0 & 0 &0 & \dots & 1 \end{pmatrix} \]

的单位矩阵。

主要步骤

  • 找到当前主元系数不为 \(0\) 的一行（这里通常也找系数绝对值较大的一行）。
  • 将这一行与当前处理到的行交换。
  • 运用初等变换将主元的系数变为 \(1\)。
  • 运用初等变换将其余行的主元的系数变为 \(0\)。

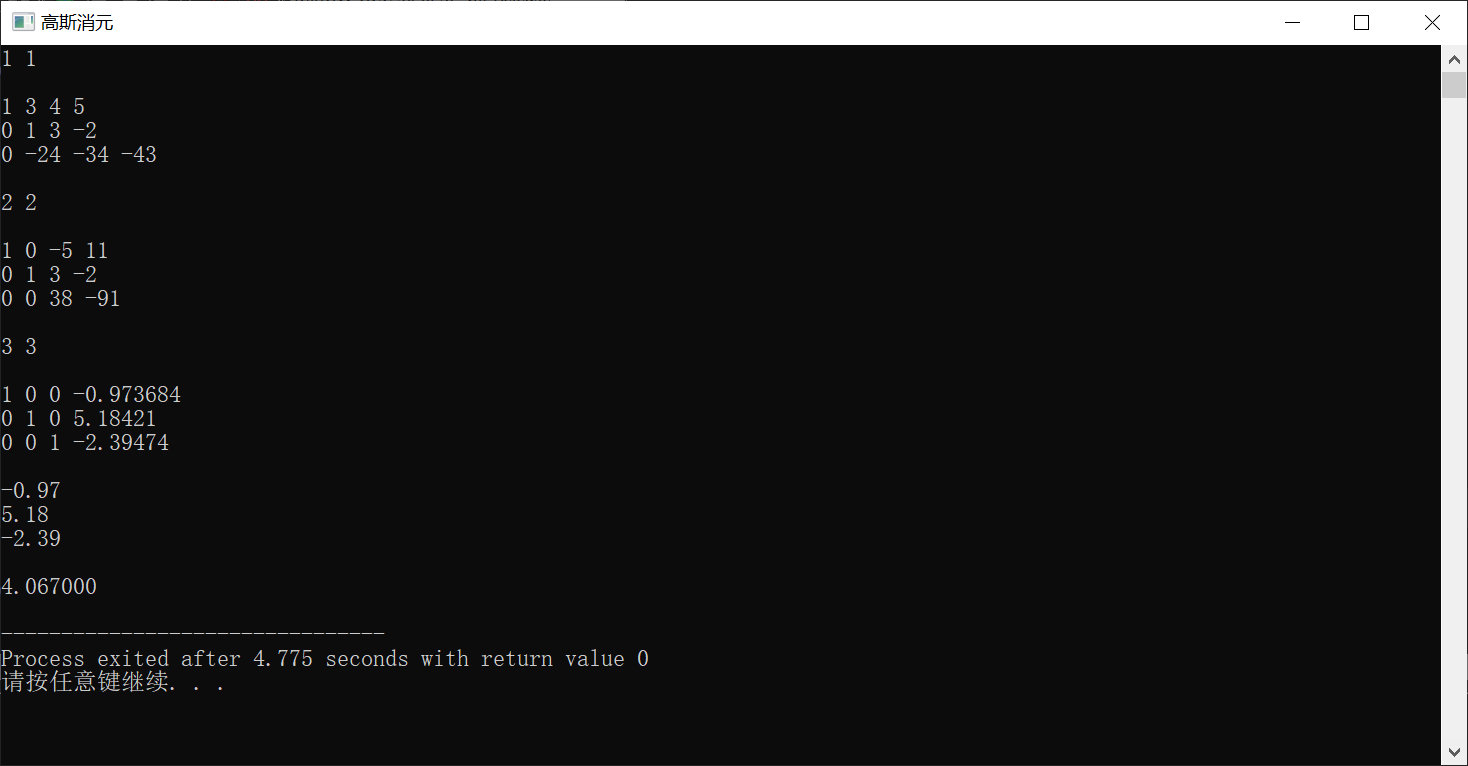
解释

追踪高斯-约当消元的执行过程。

输入：

3
1 3 4 5
1 4 7 3
9 3 2 2

输出

-0.97
5.18
-2.39

高斯-约当消元

代码实现

相比高斯消元只需改动一点，具体细节见代码。

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
#include <ctime>

using namespace std;

const int maxn = 105;
const double eps = 1e-7;//精度
double a[maxn][maxn];
double ans[maxn];
int n;

void print()
{
	puts("");
	for (int i = 1; i <= n; i++)
	{
		for (int j = 1; j <= n + 1; j++) cout << a[i][j] << " ";
		puts("");
	}
	puts("");
}//调试，输出矩阵

void gauss()
{
	//row 行 col 列
	int col = 1, row = 1;
	for (col = 1; col <= n; col++)//枚举主元所在列（1~n）
	{
		//step1 找到主元非0的一行
		int t = row;
		for (int i = row; i <= n; i++)
		{
			if (fabs(a[i][col]) > eps)
			{
				t = i;
				break;
			}
		}
		// step2
		if (fabs(a[t][col]) < eps) continue;//主元系数为0，即产生了自由元，先暂且不管
		swap(a[row], a[t]);//否则替换两行

		//step3 将主元系数置1，注意枚举顺序
		for (int i = n + 1; i >= row; i--)
		{
			a[row][i] /= a[row][col];
		}

		//step4 将所有的主元系数消为0
		for (int i = 1; i <= n; i++)
		{
			if (i == row) continue;
			for (int j = n + 1; j >= col; j--)
			{
				a[i][j] -= a[i][col] * a[row][j];
			}
		}
		//cout<<row<<" "<<col<<endl;
		//print();
		//step5 处理下一个主元
		row++;
	}

	//处理的主元个数小于n，产生了自由元，一定是无解/无穷解
	if (row <= n)
	{
		for (int i = row; i <= n; i++)
		{
			if (fabs(a[i][n + 1]) > eps)
			{
				cout << "No Solution" << endl;
				exit(0);
			}
		}
		puts("No Solution");
		exit(0);
		return;
	}
	else
	{
		//step6 输出答案
		for (int i = 1; i <= n; i++) printf("%.2lf\n", a[i][n + 1]);
	}
}




int main()
{
#ifndef ONLINE_JUDGE
#define LOCAL
	//freopen("in.txt","r",stdin);
#endif
	cin >> n;
	for (int i = 1; i <= n; i++)
	{
		for (int j = 1; j <= n + 1; j++)
		{
			scanf("%lf", &a[i][j]);
		}
	}
	gauss();
	puts("");
#ifdef LOCAL
	fprintf(stderr, "%f\n", 1.0 * clock() / CLOCKS_PER_SEC);
#endif
	return 0;
}

例题

posted @ 2025-01-13 18:47  vanueber  阅读(81)  评论(0)    收藏  举报