P2447 [SDOI2010] 外星千足虫 题解
@
[SDOI2010] 外星千足虫
题目描述
公元 \(2333\) 年 \(2\) 月 \(3\) 日,在经历了 \(17\) 年零 \(3\) 个月的漫长旅行后,“格纳格鲁一号”载人火箭返回舱终于安全着陆。此枚火箭由美国国家航空航天局(NASA)研制发射,行经火星、金星、土卫六、木卫二、谷神星、“张衡星”等 \(23\) 颗太阳系星球,并最终在小行星“杰森星”探寻到了地外生命。宇航员在“杰森星”地表岩层下 \(45.70\) 米位置发现一批珍贵的活体生命样本,并将其带回检测。
在带回的活体样本中,最吸引人的当属这些来自外星的千足虫了。这些虫子身躯纤长,身体分为若干节。受到触碰时,会将身体卷曲成圆环形,间隔一段时间后才会复原活动。
有趣的还不止如此。研究人员发现,这些虫子的足并不像地球千足虫成对出现、总共偶数条——它们每节身体下方都有着不定数量的足,但足的总数一定是奇数条!
虽然从外观难以区分二者,但通过统计足的数目,科学家们就能根据奇偶性判断出千足虫所属的星球。
作为 J 国派去 NASA 的秘密间谍,你希望参加这次研究活动以掌握进一步的情报,而 NASA 选拔的研究人员都是最优秀的科学家。于是 NASA 局长 Charles Bolden 出了一道难题来检测你的实力:
现在你面前摆有 \(1\ldots N\) 编号的 \(N\) 只千足虫,你的任务是鉴定每只虫子所属的星球,但不允许亲自去数它们的足。
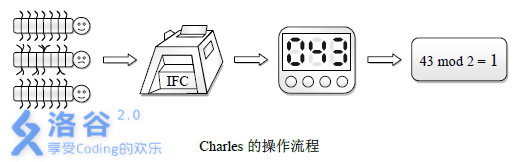
Charles 每次会在这 \(N\) 只千足虫中选定若干只放入“昆虫点足机”(the Insect Feet Counter, IFC)中,“点足机”会自动统计出其内所有昆虫足数之和。Charles 会将这个和数 \(\bmod\) \(2\) 的结果反馈给你,同时告诉你一开始放入机器中的是哪几只虫子。
他的这种统计操作总共进行 \(M\) 次,而你应当尽早得出鉴定结果。
假如在第 \(K\) 次统计结束后,现有数据就足以确定每只虫子的身份,你就还应将这个 \(K\) 反馈给 Charles,此时若 \(K<M\),则表明那后 \(M-K\) 次统计并非必须的。
如果根据所有 \(M\) 次统计数据还是无法确定每只虫子身份,你也要跟 Charles 讲明:就目前数据会存在多个解。
输入格式
第一行是两个正整数 \(N,M\)。
接下来 \(M\) 行,按顺序给出 Charles 这 \(M\) 次使用“点足机”的统计结果。每行包含一个 \(01\) 串和一个数字,用一个空格隔开。\(01\) 串按位依次表示每只虫子是否被放入机器:如果第 \(i\) 个字符是 \(0\) 则代表编号为 \(i\) 的虫子未被放入,\(1\) 则代表已被放入。后面跟的数字是统计的昆虫足数 \(\bmod\) \(2\) 的结果。
由于 NASA 的实验机器精确无误,保证前后数据不会自相矛盾。即给定数据一定有解。
输出格式
在给定数据存在唯一解时有 \(N+1\) 行,第一行输出一个不超过 \(M\) 的正整数 \(K\),表明在第 \(K\) 次统计结束后就可以确定唯一解;接下来N行依次回答每只千足虫的身份,若是奇数条足则输出 ?y7M#(火星文),偶数条足输出 Earth。
如果输入数据存在多解,输出 Cannot Determine。
样例 #1
样例输入 #1
3 5
011 1
110 1
101 0
111 1
010 1
样例输出 #1
4
Earth
?y7M#
Earth
样例 #2
样例输入 #2
5 7
01100 1
11000 1
10100 0
11100 1
00011 1
00000 0
11111 0
样例输出 #2
Cannot Determine
提示
评分标准
对于每一个测试点,如果你的输出文件与答案文件完全相同,该测试点得满分。
否则,对于存在唯一解的测试点,如果你正确回答所有千足虫的身份,将得到 \(50\%\) 的分数;
其他情况,该测试点得零分。
数据规模和约定
对于 \(20\%\) 的数据,满足 \(N=M\leq 20\);
对于 \(40\%\) 的数据,满足 \(N=M\leq 500\);
对于 \(70\%\) 的数据,满足 \(N\leq500\),\(M\leq 10^3\);
对于 \(100\%\) 的数据,满足 \(1\leq N\leq 10^3\),\(1\leq M\leq 2\times 10^3\)。
题目分析
前置芝士:高斯消元
如果不会可以看看这篇文章:数学-高斯消元
首先观察到本题的方程式在模 \(2\) 意义下进行的,所以考虑令地球千足虫的足的总数为 \(0\),外星千足虫的足的总数为 \(1\)。
因为若 \(x \equiv 1 \pmod 2\),则 \(x + 2n \equiv 1 \pmod 2\),其中 \(n\) 为正整数。与 \(0\) 同余也成立。
于是将问题转化为求解下列方程组
在模 \(2\) 意义下,上面的操作跟异或运算是等价的,即 \((a \bmod 2 + b \bmod 2) \bmod 2 = a \operatorname{xor} b\),读者可以将 \(0,1\) 分别代入验证,这里不再赘述。
于是问题转化为求
调用普通的高斯消元求解异或线性方程组即可求解出问题 \(2\) 的答案。
而对于问题 \(1\),由于题目保证数据不会出现冲突,那么如果我们用到第 \(k\) 个方程,那么前 \(k\) 个方程都不会存在冲突,于是在寻找主元时,第 \(1\) 个主元的行所在的最大行编号便是答案。
如果消元时存在主元为 \(0\) 的情况,即有多解,输出 \(\text{Cannot Determine}\) 即可。
代码实现
朴素解法
最普通的高斯消元,时间复杂度 \(O(n^2 m)\),最坏情况下无法通过此题。
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <bitset>
using namespace std;
const int maxm = 2e3 + 5;
const int maxn = 1e3 + 5;
int a[maxm][maxm];
int ans[maxn];
int n, m;
int tot = -1;
void gauss()
{
//row 行 col 列
int row = 1, col = 1;
for (col = 1; col <= n; ++col)
{
int t = row;
for (int i = row; i <= m; i++)
{
if (a[i][col])
{
t = i;
break;
}
}
if (!a[t][col])
{
puts("Cannot Determine");
exit(0);
}
tot = max(tot, t);
swap(a[row], a[t]);
for (int i = row + 1; i <= m; i++)
{
if (!a[i][col]) continue;
for (int j = n + 1; j >= col; j--)
{
a[i][j] = a[i][j] ^ a[row][j];
}
}
++row;
}
cout << tot << endl;
for (int i = n; i >= 1; i--)
{
ans[i] = a[i][n + 1];
for (int j = i + 1; j <= n; j++)
{
if (a[i][j]) ans[i] ^= ans[j];
}
}
for (int i = 1; i <= n; i++)
{
cout << (ans[i] ? "?y7M#" : "Earth") << endl;
}
return;
}
int main()
{
#ifndef ONLINE_JUDGE
#define LOCAL
//freopen("in.txt","r",stdin);
#endif
cin >> n >> m;
for (int i = 1, x; i <= m; i++)
{
for (int j = 1; j <= n; j++)
{
char y;
cin >> y;
a[i][j] = y - '0';
}
scanf("%d", &x);
a[i][n + 1] = x;
}
gauss();
#ifdef LOCAL
fprintf(stderr, "%f\n", 1.0 * clock() / CLOCKS_PER_SEC);
#endif
return 0;
}
bitset 优化
由于是异或方程组,可以使用 bitset 优化,时间复杂度 \(O(\frac{n^2 m}{\omega})\) ,其中 \(\omega = 32\)。
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <bitset>
using namespace std;
const int maxm = 2e3 + 5;
const int maxn = 1e3 + 5;
bitset<maxm> a[maxm];
int ans[maxn];
int n, m;
int tot = -1;
void gauss()
{
//row 行 col 列
int row = 1, col = 1;
for (col = 1; col <= n; ++col)
{
int t = row;
for (int i = row; i <= m; i++)
{
if (a[i].test(col))
{
t = i;
break;
}
}
if (!a[t].test(col))
{
puts("Cannot Determine");
exit(0);
}
tot = max(tot, t);
swap(a[row], a[t]);
for (int i = row + 1; i <= m; i++)
{
if (!a[i].test(col)) continue;
a[i] ^= a[row];
}
++row;
}
cout << tot << endl;
for (int i = n; i >= 1; i--)
{
ans[i] = a[i].test(n + 1);
for (int j = i + 1; j <= n; j++)
{
if (a[i].test(j)) ans[i] ^= ans[j];
}
}
for (int i = 1; i <= n; i++)
{
cout << (ans[i] ? "?y7M#" : "Earth") << endl;
}
return;
}
int main()
{
#ifndef ONLINE_JUDGE
#define LOCAL
//freopen("in.txt","r",stdin);
#endif
cin >> n >> m;
char ch;
for (int i = 1, x; i <= m; i++)
{
ch = getchar();
for (int j = 1; j <= n; j++)
{
ch = getchar();
a[i].set(j, ch - '0');
}
scanf("%d", &x);
a[i].set(n + 1, x);
}
gauss();
#ifdef LOCAL
fprintf(stderr, "%f\n", 1.0 * clock() / CLOCKS_PER_SEC);
#endif
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号