洛谷 P1219：[USACO1.5] 八皇后 Checker Challenge ← DFS
【题目来源】
【题目描述】
一个如下的 6×6 的跳棋棋盘，有六个棋子被放置在棋盘上，使得每行、每列有且只有一个，每条对角线（包括两条主对角线的所有平行线）上至多有一个棋子。
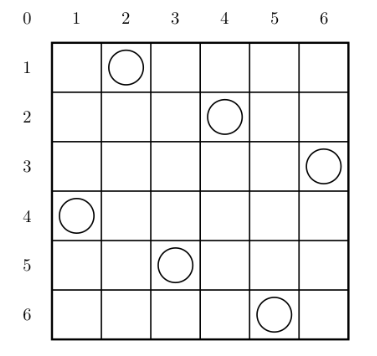
上面的布局可以用序列 2 4 6 1 3 5 来描述，第 i 个数字表示在第 i 行的相应位置有一个棋子，如下：
行号 1 2 3 4 5 6
列号 2 4 6 1 3 5
这只是棋子放置的一个解。请编一个程序找出所有棋子放置的解。
并把它们以上面的序列方法输出，解按字典顺序排列。
请输出前 3 个解。最后一行是解的总个数。
【输入格式】
一行一个正整数 n，表示棋盘是 n×n 大小的。
【输出格式】
前三行为前三个解，每个解的两个数字之间用一个空格隔开。第四行只有一个数字，表示解的总数。
【输入样例】
6
【输出样例】
2 4 6 1 3 5
3 6 2 5 1 4
4 1 5 2 6 3
4
【数据范围】
对于 100% 的数据，6≤n≤13。
【算法分析】
● 在二维矩阵中，主对角线和副对角线是两种基本的对角线方向。
（1）主对角线（左上到右下）
方向与特点：从矩阵的左上角延伸至右下角。
元素位置：位于主对角线上的所有元素，其行号（row）与列号（col）相等，即 row==col。这也是其最常见的判定方式。
公式应用：在编程中（例如解决八皇后问题），常用 row-col 的值来标识主对角线及与主对角线平行的对角线。因为，主对角线上的 row-col 是一个常数，与主对角线平行的任一对角线上的 row-col 是另外的常数。
（2）副对角线（右上到左下）
方向与特点：从矩阵的右上角延伸至左下角。它也称为反对角线或次对角线。
元素位置：位于副对角线上的所有元素，其行号（row）与列号（col）之和为定值。对于一个 n×n 的方阵，这个定值通常是 n-1，即 row+col==n-1。
公式应用：在编程中，常用 row+col 的值来标识副对角线及与副对角线平行的对角线。因为，副对角线上的 row+col 是一个常数，与副对角线平行的任一对角线上的 row+col 是另外的常数。
● 判断逻辑基于以下三个条件：
if(col[colIdx] || pdg[n-row+colIdx] || cdg[row+colIdx]) {
continue;
}
（1）列冲突检查：col[colIdx]
若为 true，表示第 colIdx 列已被其他行的皇后占用，当前位置不安全。
（2）主对角线（左上到右下）冲突检查：pdg[n-row+colIdx]
当 pdg[n-row+colIdx]=true 时 → 说明当前位置所在的【左上→右下】对角线（主对角线、或与主对角线平行的对角线）已经有皇后了，对角线冲突，直接跳过该列。该方向上的所有点满足“行索引-列索引=常数”。
C++ 中，数组的下标必须是非负整数（≥0），负数下标会直接导致程序运行报错、数组越界，这是绝对不能出现的错误！所以，原始公式 colIdx-row 不能直接作为 dg 的下标，必须做「偏移修正」，把负数全部转换成正整数！
那么，n-row+colIdx 是怎么来的？这个公式没有任何玄学，就是对原始公式做了一个正数偏移，一步变形就能得到：n-row+colIdx=(colIdx-row)+n。我们只是把 colIdx-row 的结果，整体加上了一个偏移量 n，仅此而已！
修正后的取值范围，完美适配数组下标。这是因为原始公式 colIdx-row ∈ [-(n-1), n-1]，加上偏移量n后，(colIdx-row)+n ∈ [ 1 , 2n-1 ]。所有结果全部变成了 正整数，而且没有重复、没有越界，完美满足数组下标的要求！
（3）副对角线（右上到左下）冲突检查：cdg[row+colIdx]
若 cdg[row+colIdx] 为 true，表示当前 (row, colIdx) 所在的对角线（副对角线、或与副对角线平行的对角线）已被占用。该方向上的所有点满足“行索引+列索引=常数”。
【算法代码】
#include <bits/stdc++.h>
using namespace std;
const int N=20;
bool pdg[N<<1]; //principal diagonal
bool cdg[N<<1]; //counter diagonal
int pos[N]; //Record column number where queen is placed
bool col[N];
int cnt;
int n;
void print() {
for(int i=1; i<=n; i++) {
cout<<pos[i]<<" ";
}
cout<<endl;
}
void dfs(int row) {
if(row>n) {
cnt++;
if(cnt<=3) print();
return;
}
for(int colIdx=1; colIdx<=n; colIdx++) {
if(col[colIdx] || pdg[n-row+colIdx] || cdg[row+colIdx]) {
continue;
}
pos[row]=colIdx;
col[colIdx]=pdg[n-row+colIdx]=cdg[row+colIdx]=true;
dfs(row+1); //Search the next line
col[colIdx]=pdg[n-row+colIdx]=cdg[row+colIdx]=false; //traceback
}
}
int main() {
cin>>n;
dfs(1);
cout<<cnt<<endl;
return 0;
}
/*
in:
6
out:
2 4 6 1 3 5
3 6 2 5 1 4
4 1 5 2 6 3
4
*/
【参考文献】
浙公网安备 33010602011771号