P1219 [USACO1.5] 八皇后 Checker Challenge

题目描述

一个如下的 $6 \times 6$ 的跳棋棋盘，有六个棋子被放置在棋盘上，使得每行、每列有且只有一个，每条对角线（包括两条主对角线的所有平行线）上至多有一个棋子。

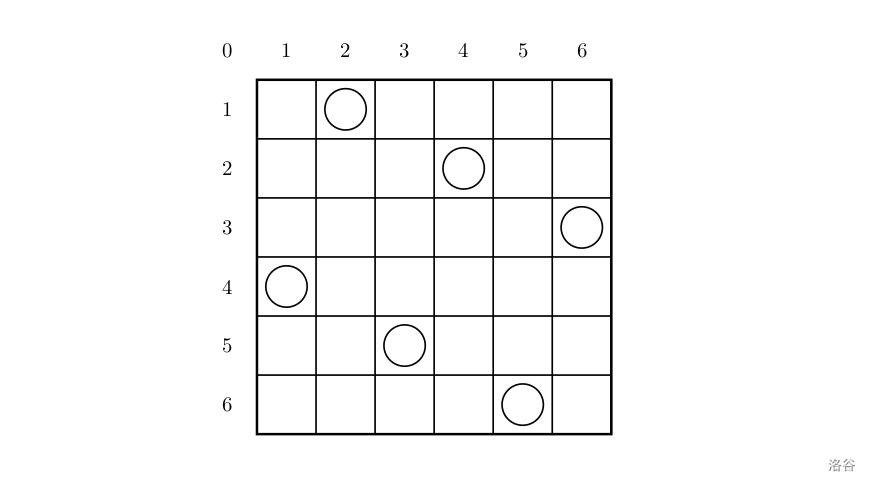
上面的布局可以用序列 $2\ 4\ 6\ 1\ 3\ 5$ 来描述，第 $i$ 个数字表示在第 $i$ 行的相应位置有一个棋子，如下：

行号 $1\ 2\ 3\ 4\ 5\ 6$

列号 $2\ 4\ 6\ 1\ 3\ 5$

这只是棋子放置的一个解。请编一个程序找出所有棋子放置的解。
并把它们以上面的序列方法输出，解按字典顺序排列。
请输出前 $3$ 个解。最后一行是解的总个数。

输入格式

一行一个正整数 $n$，表示棋盘是 $n \times n$ 大小的。

输出格式

前三行为前三个解，每个解的两个数字之间用一个空格隔开。第四行只有一个数字，表示解的总数。

输入输出样例 #1

输入 #1

6

输出 #1

2 4 6 1 3 5
3 6 2 5 1 4
4 1 5 2 6 3
4

说明/提示

【数据范围】
对于 $100%$ 的数据，$6 \le n \le 13$。

题目翻译来自NOCOW。

USACO Training Section 1.5

---

对角线规律

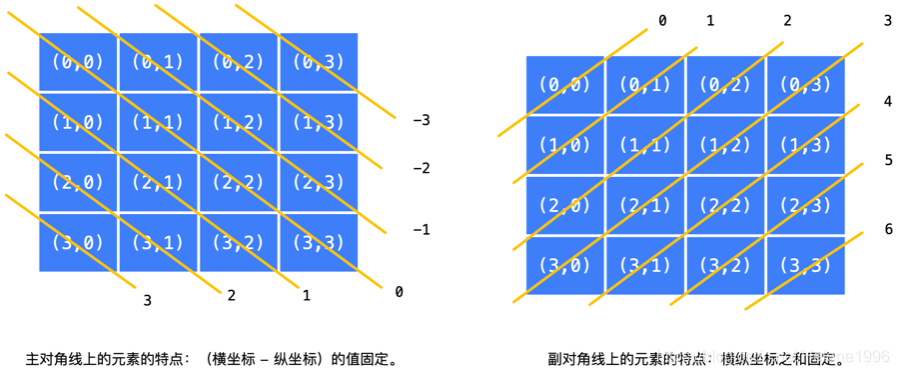
y=-x+b 、u=-i +b
y=x+b、u = i +b
可以用差值做为下标建立一个集合。我们落定一个皇后时，数组下标为皇后下标差值的设为false。这样其他对角线元素就可以检测后不落定

u对应纵坐标，i对应恒坐标

由于反对角线差值有负数，可以+一个绝对值n，也就是
n+i-u

#include <cstdio>
#include <iostream>

using namespace std;

const int N =20;

int n;
char g[N];
bool col[N],dg[N],udg[N]; //记录已经填过的数 

int x=0; // 第几个解
int sum = 0; // 一共多少个解

// u 递归深度 
void dfs(int u){
	 
    // 递归到底，输出
    if (u == n) {
        x++;
        sum++;
        if(x<=3){
            for(int i=0;i<n;i++)
			    printf("%d ",g[i]);
		    puts("");
        }
		return;
    }
    
	for(int i=0;i<n;i++)
		// 广度遍历
		if(!col[i] && !dg[u+i]&& !udg[n-u+i]){
			// 如果行列斜未有则落定
			g[u] = i+1; // 下标偏移1，从1始
			udg[n+i-u] = col[i] = dg[u+i] = true; // 行列斜标记
			dfs(u+1); // 深度优先
			udg[n+i-u] = col[i] = dg[u+i] = false; // 为广度恢复现场
		} 
}

int main(){
	cin >> n;
	dfs(0); 
    printf("%d",sum);
	return 0;
}