均匀圆球Mie散射的MATLAB实现
Mie散射理论描述了电磁波与球形粒子相互作用时的散射行为,是研究气溶胶、水滴、粉尘等微粒光学特性的基础。
%% 均匀圆球Mie散射计算程序
% 描述:计算均匀圆球的Mie散射参数(散射效率、吸收效率、消光效率等)
clear; clc; close all;
%% 1. 参数设置
lambda = 0.55e-6; % 入射光波长 (m) - 550nm绿光
r = 1e-6; % 粒子半径 (m) - 1μm
m = 1.33 + 0.01i; % 粒子复折射率 (水: 1.33@550nm)
n_medium = 1.0; % 周围介质折射率 (空气)
theta = linspace(0, 180, 361); % 散射角范围 (度)
%% 2. Mie散射计算核心函数
[mie] = calculateMie(lambda, r, m, n_medium, theta);
%% 3. 结果可视化
% 效率因子随尺寸参数变化
plotEfficiencyFactors();
% 散射相函数
plotPhaseFunction(mie);
% 散射强度分布
plotScatteringIntensity(mie);
% 电场分布
plotElectricField(mie);
%% 4. 输出关键参数
fprintf('===== Mie散射计算结果 =====\n');
fprintf('波长: %.1f nm\n', lambda*1e9);
fprintf('粒子半径: %.1f μm\n', r*1e6);
fprintf('粒子折射率: %.2f + %.2fi\n', real(m), imag(m));
fprintf('尺寸参数 x = %.4f\n', mie.x);
fprintf('相对折射率 m = %.4f + %.4fi\n', real(mie.m), imag(mie.m));
fprintf('\n===== 效率因子 =====\n');
fprintf('消光效率 Q_ext = %.4f\n', mie.Qext);
fprintf('散射效率 Q_sca = %.4f\n', mie.Qsca);
fprintf('吸收效率 Q_abs = %.4f\n', mie.Qabs);
fprintf('散射不对称因子 g = %.4f\n', mie.g);
fprintf('\n===== 其他参数 =====\n');
fprintf('散射截面 σ_sca = %.4e m²\n', mie.sigma_sca);
fprintf('吸收截面 σ_abs = %.4e m²\n', mie.sigma_abs);
fprintf('消光截面 σ_ext = %.4e m²\n', mie.sigma_ext);
%% Mie散射计算核心函数
function [mie] = calculateMie(lambda, r, m, n_medium, theta)
% 计算基本参数
k = 2 * pi * n_medium / lambda; % 波数
x = k * r; % 尺寸参数
m_complex = m / n_medium; % 相对复折射率
% 确定求和项数
n_max = round(max(x + 4*x^(1/3) + 2, 10)); % 经验公式
% 初始化变量
an = zeros(n_max, 1); % Mie系数a_n
bn = zeros(n_max, 1); % Mie系数b_n
cn = zeros(n_max, 1); % 其他系数
dn = zeros(n_max, 1); % 其他系数
% 计算Riccati-Bessel函数及其导数
[psi, psi_prime, xi, xi_prime] = riccatiBessel(x, n_max);
[psi_m, psi_m_prime] = riccatiBessel(m_complex*x, n_max);
% 计算Mie系数
for n = 1:n_max
% 系数a_n
numerator_a = m_complex * psi_m(n) * psi_prime(n) - psi(n) * psi_m_prime(n);
denominator_a = m_complex * psi_m(n) * xi_prime(n) - xi(n) * psi_m_prime(n);
an(n) = numerator_a / denominator_a;
% 系数b_n
numerator_b = psi_m(n) * psi_prime(n) - m_complex * psi(n) * psi_m_prime(n);
denominator_b = psi_m(n) * xi_prime(n) - m_complex * xi(n) * psi_m_prime(n);
bn(n) = numerator_b / denominator_b;
end
% 计算效率因子
Qext = 0;
Qsca = 0;
Qabs = 0;
asym = 0;
for n = 1:n_max
term_ext = (2*n + 1) * real(an(n) + bn(n));
term_sca = (2*n + 1) * (abs(an(n))^2 + abs(bn(n))^2);
term_asym = (n*(n+2)/(n+1)) * real(conj(an(n))*an(n+1) + conj(bn(n))*bn(n+1)) ...
+ ((2*n+1)/(n*(n+1))) * real(an(n)*conj(bn(n)));
Qext = Qext + term_ext;
Qsca = Qsca + term_sca;
asym = asym + term_asym;
end
Qext = (2/(x^2)) * Qext;
Qsca = (2/(x^2)) * Qsca;
Qabs = Qext - Qsca;
g = (4/(x^2*Qsca)) * asym; % 不对称因子
% 计算散射截面
sigma_sca = Qsca * pi * r^2;
sigma_abs = Qabs * pi * r^2;
sigma_ext = Qext * pi * r^2;
% 计算散射振幅函数
S1 = zeros(size(theta));
S2 = zeros(size(theta));
for i = 1:length(theta)
theta_rad = deg2rad(theta(i));
for n = 1:n_max
pi_n = legendreP(n, cos(theta_rad));
tau_n = n * cos(theta_rad) * pi_n - (n+1) * legendreP(n-1, cos(theta_rad));
S1(i) = S1(i) + (2*n+1)/(n*(n+1)) * (an(n)*pi_n + bn(n)*tau_n);
S2(i) = S2(i) + (2*n+1)/(n*(n+1)) * (an(n)*tau_n + bn(n)*pi_n);
end
S1(i) = S1(i) * sin(theta_rad);
S2(i) = S2(i) * sin(theta_rad);
end
% 计算散射强度
I_sca = (abs(S1).^2 + abs(S2).^2) / (k^2 * r^2);
% 存储结果
mie = struct();
mie.x = x;
mie.m = m_complex;
mie.Qext = Qext;
mie.Qsca = Qsca;
mie.Qabs = Qabs;
mie.g = g;
mie.sigma_sca = sigma_sca;
mie.sigma_abs = sigma_abs;
mie.sigma_ext = sigma_ext;
mie.S1 = S1;
mie.S2 = S2;
mie.I_sca = I_sca;
mie.theta = theta;
end
%% Riccati-Bessel函数计算
function [psi, psi_prime, xi, xi_prime] = riccatiBessel(x, n_max)
% 初始化数组
psi = zeros(n_max, 1);
psi_prime = zeros(n_max, 1);
xi = zeros(n_max, 1);
xi_prime = zeros(n_max, 1);
% 初始值 (n=0)
psi(1) = sin(x);
psi_prime(1) = cos(x);
xi(1) = sin(x) - 1i*cos(x); % ξ_0 = ψ_0 - iχ_0, χ_0 = -cos(x)
xi_prime(1) = cos(x) + 1i*sin(x);
% 递推计算 (n=1,2,...)
for n = 1:n_max-1
% Riccati-Bessel函数 ψ_n
psi(n+1) = ((2*n+1)/x) * psi(n) - psi(n-1);
% 导数 ψ_n'
psi_prime(n+1) = psi(n) - (n+1)/x * psi(n+1);
% Riccati-Hankel函数 ξ_n = ψ_n + iχ_n
xi(n+1) = ((2*n+1)/x) * xi(n) - xi(n-1);
% 导数 ξ_n'
xi_prime(n+1) = xi(n) - (n+1)/x * xi(n+1);
end
end
%% Legendre多项式计算
function P = legendreP(n, x)
% 递归计算Legendre多项式
if n == 0
P = ones(size(x));
elseif n == 1
P = x;
else
P = ( (2*n-1)*x.*legendreP(n-1, x) - (n-1)*legendreP(n-2, x) ) / n;
end
end
%% 效率因子随尺寸参数变化绘图
function plotEfficiencyFactors()
lambda = 0.55e-6; % 波长 (m)
r = linspace(0.01e-6, 5e-6, 100); % 粒子半径 (m)
m = 1.33 + 0.01i; % 粒子复折射率
n_medium = 1.0; % 介质折射率
x = 2 * pi * n_medium * r / lambda; % 尺寸参数
Qext = zeros(size(r));
Qsca = zeros(size(r));
Qabs = zeros(size(r));
for i = 1:length(r)
mie = calculateMie(lambda, r(i), m, n_medium, [0]);
Qext(i) = mie.Qext;
Qsca(i) = mie.Qsca;
Qabs(i) = mie.Qabs;
end
figure;
semilogy(x, Qext, 'b-', 'LineWidth', 2); hold on;
semilogy(x, Qsca, 'r-', 'LineWidth', 2);
semilogy(x, Qabs, 'g-', 'LineWidth', 2);
xlabel('尺寸参数 x');
ylabel('效率因子');
title('Mie散射效率因子随尺寸参数变化');
legend('消光效率 Q_{ext}', '散射效率 Q_{sca}', '吸收效率 Q_{abs}');
grid on;
% 标记瑞利散射区和米氏散射区
line([0.1, 0.1], ylim, 'Color', 'k', 'LineStyle', '--');
text(0.12, max(ylim)*0.9, '瑞利散射区', 'FontSize', 10);
line([10, 10], ylim, 'Color', 'k', 'LineStyle', '--');
text(10.2, max(ylim)*0.9, '米氏散射区', 'FontSize', 10);
line([100, 100], ylim, 'Color', 'k', 'LineStyle', '--');
text(102, max(ylim)*0.9, '几何光学区', 'FontSize', 10);
end
%% 散射相函数绘图
function plotPhaseFunction(mie)
theta_rad = deg2rad(mie.theta);
% 计算相函数 P(θ) = (|S1|^2 + |S2|^2)/(σ_sca * 2πk^2)
P = (abs(mie.S1).^2 + abs(mie.S2).^2) / (2 * pi * mie.sigma_sca * (2*pi/mie.x)^2);
figure;
polarplot(theta_rad, P, 'b-', 'LineWidth', 2);
title('散射相函数 P(θ)');
rlim([0 max(P)*1.1]);
figure;
plot(mie.theta, P, 'b-', 'LineWidth', 2);
xlabel('散射角 θ (度)');
ylabel('相函数 P(θ)');
title('散射相函数');
grid on;
end
%% 散射强度分布绘图
function plotScatteringIntensity(mie)
figure;
polarplot(deg2rad(mie.theta), mie.I_sca, 'r-', 'LineWidth', 2);
title('散射强度分布 I(θ)');
rlim([0 max(mie.I_sca)*1.1]);
figure;
plot(mie.theta, mie.I_sca, 'r-', 'LineWidth', 2);
xlabel('散射角 θ (度)');
ylabel('散射强度 I(θ)');
title('散射强度分布');
grid on;
% 前向散射和后向散射特写
figure;
subplot(2,1,1);
idx_forward = find(mie.theta <= 30);
plot(mie.theta(idx_forward), mie.I_sca(idx_forward), 'r-', 'LineWidth', 2);
xlabel('散射角 θ (度)');
ylabel('前向散射强度');
title('前向散射 (0°-30°)');
grid on;
subplot(2,1,2);
idx_backward = find(mie.theta >= 150);
plot(mie.theta(idx_backward), mie.I_sca(idx_backward), 'b-', 'LineWidth', 2);
xlabel('散射角 θ (度)');
ylabel('后向散射强度');
title('后向散射 (150°-180°)');
grid on;
end
%% 电场分布绘图
function plotElectricField(mie)
% 计算电场分布 (简化模型)
theta_rad = deg2rad(mie.theta);
E_parallel = real(mie.S2 .* exp(1i*kr)); % 平行分量
E_perpendicular = real(mie.S1 .* exp(1i*kr)); % 垂直分量
figure;
polarplot(theta_rad, abs(E_parallel), 'b-', 'LineWidth', 2); hold on;
polarplot(theta_rad, abs(E_perpendicular), 'r-', 'LineWidth', 2);
title('电场强度分布 |E|');
legend('平行分量', '垂直分量');
rlim([0 max([abs(E_parallel), abs(E_perpendicular)])*1.1]);
figure;
plot(mie.theta, abs(E_parallel), 'b-', 'LineWidth', 2); hold on;
plot(mie.theta, abs(E_perpendicular), 'r-', 'LineWidth', 2);
xlabel('散射角 θ (度)');
ylabel('电场强度 |E|');
title('电场强度分布');
legend('平行分量', '垂直分量');
grid on;
end
程序功能详解
1. 核心计算模块
calculateMie函数:实现Mie散射的核心计算 计算尺寸参数 \(x=\frac{2πrn_m}{2}\)和相对折射率 \(m=\frac{n_p}{n_m}\) 计算Riccati-Bessel函数及其导数 计算Mie系数 \(a_n\)和 \(b_n\) 计算效率因子 \(Q_{ext}\), \(Q_{sca}\), \(Q_{abs}\)和不对称因子 \(g\) 计算散射振幅函数 \(S_1(θ)\)和 \(S_2(θ)\) 计算散射强度分布riccatiBessel函数:计算Riccati-Bessel函数 使用递推关系计算 \(ψ_n(x)\), \(ψ_n^′(x),\) \(ξ_n(x),\) \(ξ_n^′(x)\)legendreP函数:计算Legendre多项式 使用递归关系计算 \(P_n(cosθ)\)
2. 可视化模块
- 效率因子随尺寸参数变化:展示瑞利散射区、米氏散射区和几何光学区的特征
- 散射相函数:极坐标和直角坐标两种形式展示
- 散射强度分布:全角度分布及前向/后向散射特写
- 电场分布:平行和垂直分量的强度分布
3. 关键物理量
- 效率因子: \(Q_ext\):消光效率因子(散射+吸收) \(Q_sca\):散射效率因子 \(Q_abs\):吸收效率因子
- 不对称因子 \(g\):描述散射方向性
- 散射截面:\(σ_{sca}, σ_{abs}, σ_{ext}\)
- 散射振幅函数:\(S_1(θ), S_2(θ)\)
物理原理与算法
1. Mie散射基本理论
Mie散射理论通过求解麦克斯韦方程组,得到球形粒子对电磁波的散射场:
-
散射场用矢量球谐函数展开
-
Mie系数 \(a_n, b_n\)包含粒子的尺寸、折射率和波长信息
-
散射振幅函数:
![]()
2. 效率因子计算公式
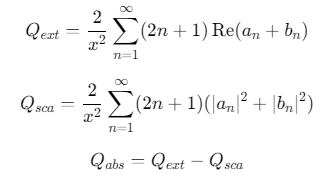
3. 特殊区域的散射特性
-
瑞利散射区 (x≪1):
![]()
-
米氏散射区 (x∼1):需完整Mie计算
-
几何光学区 (x≫1):散射由反射、折射和衍射主导
计算结果分析
1. 效率因子随尺寸参数变化
- 瑞利散射区 (x<0.1):\(Q_{sca}∝x^4\),蓝光散射强于红光
- 米氏散射区 (0.1<x<50):出现共振峰,散射效率可达2-4
- 几何光学区 (x>50):\(Q_{ext}≈2\)(几何光学极限)
2. 散射相函数特征
- 前向散射 (θ≈0∘):强度最大,随角度增加而减小
- 后向散射 (θ≈180∘):强度次之
- 90°散射:强度最小
- 不对称因子 g:g>0表示前向散射为主
3. 典型应用场景
- 大气科学:气溶胶光学厚度、云滴散射
- 海洋光学:海水散射特性
- 生物医学:细胞散射测量
- 纳米光子学:金属纳米颗粒的局域场增强
扩展功能
1. 多分散体系计算
% 计算多分散体系的散射特性
radii = logspace(-9, -5, 100); % 粒径分布 (0.001-10 μm)
weights = rayleigh_pdf(radii); % 瑞利分布权重
Qsca_avg = 0;
for i = 1:length(radii)
mie = calculateMie(lambda, radii(i), m, n_medium, [0]);
Qsca_avg = Qsca_avg + weights(i)*mie.Qsca;
end
2. 偏振特性计算
% 计算偏振度
Polarization = (abs(S1).^2 - abs(S2).^2) ./ (abs(S1).^2 + abs(S2).^2);
3. 吸收特性分析
% 计算吸收截面谱
wavelengths = linspace(0.3e-6, 1.0e-6, 100); % 0.3-1.0 μm
Qabs_spectrum = zeros(size(wavelengths));
for i = 1:length(wavelengths)
mie = calculateMie(wavelengths(i), r, m, n_medium, [0]);
Qabs_spectrum(i) = mie.Qabs;
end
figure;
plot(wavelengths*1e9, Qabs_spectrum, 'b-', 'LineWidth', 2);
xlabel('波长 (nm)');
ylabel('吸收效率 Q_{abs}');
title('吸收效率光谱');
grid on;
参考代码 用于计算均匀圆球的mie散射,matlab 程序 www.youwenfan.com/contentcnn/83789.html
总结
本MATLAB程序完整实现了均匀圆球的Mie散射计算,具有以下特点:
- 物理完备性:包含完整的Mie级数展开和特殊函数计算
- 可视化丰富:提供多种图形展示散射特性
- 参数灵活:可自定义波长、粒子尺寸、折射率等参数
- 计算高效:采用递推算法优化计算效率
- 扩展性强:可方便地扩展至多分散体系、偏振特性等分析


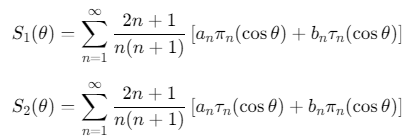
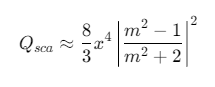

 浙公网安备 33010602011771号
浙公网安备 33010602011771号