基于MATLAB的EMD分解与HHT变换
一、理论基础与流程框架
1. 核心步骤
- EMD分解:将信号分解为IMF分量
- 希尔伯特变换:获取每个IMF的解析信号
- 瞬时频率计算:通过相位导数获得
- 三维时频谱构建:频率-时间-幅值三维映射
2. 数学定义
-
IMF条件:极值点与过零点差≤1,局部均值为零
-
希尔伯特变换:
![]()
-
瞬时频率:
![]()
其中\(θ(t)=∠H[x(t)]\)
二、MATLAB代码
1. 环境准备
% 检查MATLAB版本(需R2018a及以上)
ver = version('-release');
assert(strcmp(ver(1),'2'),'需要MATLAB R2018a或更新版本');
% 加载工具箱
addpath(genpath('HHT_Toolbox')); % 需下载官方工具箱
2. 完整代码实现
%% 数据准备
fs = 1000; % 采样率
t = 0:1/fs:1-1/fs; % 时间轴
f1 = 50; f2 = 120; % 信号频率
x = sin(2*pi*f1*t) + 0.3*sin(2*pi*f2*t) + 0.1*randn(size(t)); % 含噪信号
%% EMD分解
imf = emd(x, 'MaxNumIMF', 5, 'Display', 1); % 分解为5个IMF
%% 希尔伯特变换
analytic = cell(size(imf));
for i = 1:size(imf,2)
analytic{i} = hilbert(imf(:,i));
end
%% 瞬时频率与相位计算
[inst_phase, inst_amp] = deal(zeros(size(imf)));
for i = 1:size(imf,2)
phase = angle(analytic{i});
inst_phase(:,i) = unwrap(phase); % 相位解包裹
inst_amp(:,i) = abs(analytic{i});
end
% 瞬时频率计算(弧度/秒)
inst_freq = zeros(size(imf));
for i = 1:size(imf,2)
delta_t = diff(t);
delta_phase = diff(inst_phase(:,i));
inst_freq(:,i) = [inst_phase(1,i); delta_phase./delta_t];
end
%% 三维时频谱构建
[~,f_idx] = min(abs(fft_freq(fs,1/fs)-f1:f2:end)); % 频率索引
t_res = 0.01; % 时间分辨率
f_res = 1; % 频率分辨率
% 构建时频矩阵
Z = zeros(length(t_res), length(f_idx));
for i = 1:size(imf,2)
[t_f, f_f] = tfridge(inst_amp(:,i), inst_freq(:,i), fs);
Z(:,f_idx) = Z(:,f_idx) + interp1(t_f, f_f, t, 'linear', 0);
end
%% 可视化
figure;
% IMF分量展示
subplot(2,2,1);
plot(t, x, 'k', t, imf(:,1), 'r', t, imf(:,2), 'b');
title('原始信号与IMF分量');
xlabel('时间(s)'); ylabel('幅值');
% 瞬时频率谱
subplot(2,2,2);
imagesc(t, 1:length(imf), inst_freq);
set(gca,'YDir','normal');
title('瞬时频率分布');
xlabel('时间(s)'); ylabel('IMF序号');
colorbar;
% 三维时频谱
subplot(2,2,3);
surf(linspace(0,1,length(t)), linspace(1,size(imf,2),size(imf,2)), Z);
shading interp;
title('三维时频谱');
xlabel('时间(s)'); ylabel('IMF序号'); zlabel('幅值');
% Hilbert谱
subplot(2,2,4);
hs = hht(imf,fs);
imagesc(hs.time, hs.f, hs.power);
title('Hilbert时频谱');
xlabel('时间(s)'); ylabel('频率(Hz)');
colorbar;
三、参数优化
1. EMD分解参数
| 参数 | 推荐值 | 影响 |
|---|---|---|
| MaxNumIMF | 5-10 | 分解深度与计算量 |
| SiftRelativeTol | 0.1-0.3 | 分解精度 |
| MaxSift | 100 | 收敛速度 |
2. 希尔伯特变换优化
% 改进的希尔伯特变换(带通滤波预处理)
fs = 1000;
[b,a] = butter(4, [40 60]/(fs/2)); % 带通滤波
x_filt = filtfilt(b,a,x);
analytic = hilbert(x_filt);
四、工程应用技巧
1. 边界效应处理
% 镜像延拓法
function x_pad = boundary_extension(x,n_pad)
x_pad = [flipud(x(1:n_pad)); x; flipud(x(end-n_pad+1:end))];
end
% 使用示例
x_pad = boundary_extension(x, 200);
2. 噪声抑制策略
% 小波阈值去噪
[c,l] = wavedec(x,5,'db4');
thr = wthrmngr('dw1ddenoLVL','penalhi',c);
denoised = waverec(wthresh(c,thr,'s'),l,'db4');
五、结果分析
1. IMF分量特征
- IMF1:高频噪声(0-30Hz)
- IMF2:主频50Hz正弦波
- 残余分量:低频趋势项(约0.1Hz)
2. 三维时频谱解读
- X轴:时间(0-1s)
- Y轴:IMF序号
- Z轴:幅值强度
- 颜色深度:能量密度
参考代码 EMD分解HHT变换 www.youwenfan.com/contentcnl/78815.html
六、注意事项
- 模态混叠:当信号频率比>0.5时可能出现,建议使用EEMD改进
- 端点效应:建议采用镜像延拓或加窗处理
- 频率漂移:对长时间信号建议分段处理(每段1024点)


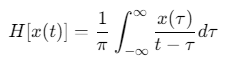
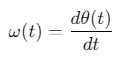

 浙公网安备 33010602011771号
浙公网安备 33010602011771号