基于MATLAB的梯度投影稀疏重建算法

基于MATLAB的梯度投影稀疏重建算法（GPSR）是压缩感知领域的核心方法之一，其通过梯度下降与投影操作的结合实现稀疏信号的高效恢复。

---

一、GPSR算法原理与数学模型

1. 优化问题建模

GPSR用于解决以下L1范数最小化问题：

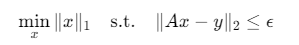
其中：

2. 等价二次规划形式

通过变量分离法将问题转化为：

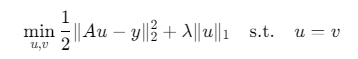
引入辅助变量v后，构建增广拉格朗日函数：

---

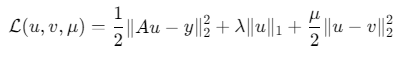
二、实现步骤

1. 算法框架

function [x_recon, history] = GPSR(A, y, lambda, max_iter, tol)
    % 输入参数：
    % A: 测量矩阵 (m x n)
    % y: 观测向量 (m x 1)
    % lambda: 正则化参数
    % max_iter: 最大迭代次数
    % tol: 收敛阈值
    
    % 初始化
    [m, n] = size(A);
    x = zeros(n, 1);
    u = x;
    v = x;
    history.obj = zeros(max_iter, 1);
    
    % 主迭代循环
    for k = 1:max_iter
        % 计算梯度
        grad = A' * (A * u - y);
        
        % 更新u
        u_new = sign(u) .* max(abs(u) - lambda, 0);
        
        % 投影到约束空间
        v_new = (u_new + v)/2;
        
        % 更新拉格朗日乘子
        mu = 0.5 * (norm(A*(v_new - u_new))^2) / (2*norm(A*(v_new - u_new))^2 + 1e-10);
        
        % 收敛判断
        history.obj(k) = 0.5*norm(A*u_new - y)^2 + lambda*norm(u_new,1);
        if norm(u_new - u) < tol
            break;
        end
        
        % 更新变量
        u = u_new;
        v = v_new;
    end
    
    x_recon = u_new;
end

2. 关键参数说明

• 正则化参数λ：控制稀疏性与数据保真度的权衡，可通过交叉验证选择（典型值范围：0.01-1）
• 收敛阈值tol：建议设置为1e-5~1e-6
• 最大迭代次数max_iter：一般不超过1000次

---

三、应用案例：图像压缩感知

1. 实验设置

% 参数设置
N = 256;          % 图像尺寸
k = 10;           % 稀疏度
m = round(N/2);   % 测量数
A = randn(m, N);  % 高斯测量矩阵

% 生成测试图像（稀疏表示）
x = zeros(N,1);
x(randperm(N, k)) = randn(k,1);
X = dct(x);       % DCT变换

% 生成观测数据
y = A * X;

% 添加高斯噪声
noise_level = 0.05;
y = y + noise_level*randn(size(y));

2. 重构与可视化

% 运行GPSR算法
lambda = 0.1;
max_iter = 500;
[x_recon, history] = GPSR(A, y, lambda, max_iter, 1e-6);

% 逆DCT变换
X_recon = x_recon;
x_recon_img = idct(X_recon);

% 计算PSNR
mse = mean((x - x_recon_img).^2);
psnr_val = 10*log10(255^2/mse);
disp(['PSNR: ', num2str(psnr_val), ' dB']);

% 显示结果
figure;
subplot(1,2,1);
imshow(x, []);
title('原始图像');
subplot(1,2,2);
imshow(x_recon_img, []);
title(['重构图像 (PSNR: ', num2str(psnr_val), ' dB)']);

参考代码 压缩感知或稀疏表示中的梯度投影稀疏重建算法 www.youwenfan.com/contentcni/64341.html

四、改进方向与扩展

1. 非凸优化扩展

• Lp范数正则化（0 < p < 1）增强稀疏性：

  % 修改目标函数为Lp范数
  obj = sum(abs(u).^p) + lambda*norm(A*u - y,2)^2;
  

• 交替方向乘子法（ADMM）处理复合优化问题

2. 深度学习融合

构建端到端网络加速重构：

layers = [
    imageInputLayer([N N 1])
    convolution2dLayer(3, 64, 'Padding', 'same')
    reluLayer
    convolution2dLayer(3, 1, 'Padding', 'same')
    regressionLayer];

3. 硬件加速方案

• GPU并行计算：使用gpuArray加速矩阵运算

  A_gpu = gpuArray(A);
  y_gpu = gpuArray(y);
  [x_recon_gpu, ~] = GPSR(A_gpu, y_gpu, lambda, max_iter, tol);
  x_recon = gather(x_recon_gpu);