MATLAB在卫星姿态控制系统中的应用

卫星姿态控制是确保卫星完成对地观测、通信、导航等任务的核心环节，其设计需应对非线性动力学、外部扰动（如太阳光压、大气阻力）、执行机构限制等挑战。MATLAB作为航天工程领域的主流仿真工具，通过Simulink可视化建模、ODE45数值求解、控制算法集成等功能，为卫星姿态控制系统的设计、验证提供了高效平台。本文将详细介绍MATLAB在卫星姿态控制系统中的应用，涵盖模型建立、控制算法实现、仿真验证全流程，并结合具体案例说明。

---

一、卫星姿态控制系统的MATLAB建模

卫星姿态控制系统的模型是仿真的基础，主要包括姿态动力学模型、运动学模型、传感器模型和执行机构模型。MATLAB通过符号计算（如Symbolic Math Toolbox）或数值方法（如ODE45）实现这些模型的构建。

1. 姿态动力学模型：描述卫星姿态变化的物理规律

卫星姿态动力学遵循牛顿-欧拉方程，核心是角动量守恒。对于刚体卫星，动力学方程可表示为：

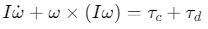
其中：

• \(I\)：卫星的转动惯量矩阵（对角矩阵，单位：\(kg⋅m^2\)）；
• \(ω\)：卫星的角速度向量（单位：\(rad/s\)）；
• \(τ_c\)：控制力矩（由执行机构产生，单位：\(N⋅m\)）；
• \(τ_d\)：外部扰动力矩（如太阳光压、大气阻力，单位：\(N⋅m\)）。

MATLAB实现：

通过符号计算定义转动惯量矩阵和控制力矩，例如：

syms Ixx Iyy Izz  % 转动惯量（对角元素）
I = diag([Ixx, Iyy, Izz]);  % 转动惯量矩阵
omega = [omega_x; omega_y; omega_z];  % 角速度向量
tau_c = [tau_cx; tau_cy; tau_cz];  % 控制力矩
tau_d = [tau_dx; tau_dy; tau_dz];  % 外部扰动力矩

% 动力学方程
dynamics = I*diff(omega) + cross(omega, I*omega) - tau_c - tau_d;

对于非线性动力学（如大角度姿态机动），可通过ode45函数数值求解

2. 姿态运动学模型：描述姿态与角速度的关系

运动学模型用于将角速度转换为姿态角（如欧拉角、四元数），或反之。常用的姿态表示方法有：

• 欧拉角（\(Roll-Pitch-Yaw，ϕ−θ−ψ\)）：直观但存在奇点（如θ=±90∘）；
• 四元数（\(q0−q1−q2−q3\)）：无奇点，适合大角度姿态描述。

四元数运动学方程：

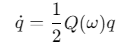
其中\(Q(ω)\)是四元数与角速度的转换矩阵：

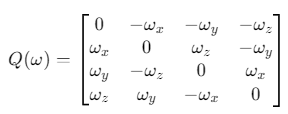
MATLAB实现：

通过函数定义四元数运动学方程，例如：

function dq = quaternion_kinematics(q, omega)
    % q: 四元数 [q0, q1, q2, q3]（标量在前）
    % omega: 角速度 [omega_x, omega_y, omega_z]
    Q = [0, -omega(1), -omega(2), -omega(3);
         omega(1), 0, omega(3), -omega(2);
         omega(2), -omega(3), 0, omega(1);
         omega(3), omega(2), -omega(1), 0];
    dq = 0.5 * Q * q;
end

3. 传感器模型：模拟姿态测量设备

卫星姿态测量常用陀螺仪（测角速度）、星敏感器（测姿态角）。传感器模型需考虑噪声（如陀螺仪的常值漂移、星敏感器的随机噪声）。

陀螺仪模型：

\(ω_m=ω+b_g+n_g\)

其中：

• \(ω_m\)：陀螺仪测量值；
• \(b_g\)：常值漂移（单位：rad/s）；
• \(n_g\)：高斯白噪声（单位：rad/s）。

星敏感器模型：

\(q_m=q+n_q\)

其中\(n_q\)是姿态四元数的测量噪声（单位：无）。

MATLAB实现：

通过awgn函数添加噪声，例如：

% 陀螺仪测量值（含噪声）
omega_m = omega + [0.01; 0.01; 0.01] + 0.001*randn(3,1);  % b_g=[0.01,0.01,0.01] rad/s，n_g=0.001*randn

% 星敏感器测量值（含噪声）
q_m = q + 0.001*randn(4,1);  % n_q=0.001*randn

4. 执行机构模型：模拟控制力矩产生

执行机构用于产生控制力矩，常用反作用轮（RW）、磁力矩器（MT）。反作用轮的力矩输出与角加速度成正比，磁力矩器的力矩与地磁场和磁矩的叉乘成正比。

反作用轮模型：

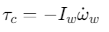
其中\(I_w\)是反作用轮的转动惯量，\(ω˙_w\)是反作用轮的角加速度。

MATLAB实现：

通过积分反作用轮的角加速度得到角速度，再计算控制力矩：

% 反作用轮参数
I_w = 0.1;  % 转动惯量 (kg·m²)
omega_w0 = 0;  % 初始角速度 (rad/s)

% 控制力矩输入（由控制器输出）
tau_c = [1; 0; 0];  % 示例：x轴方向1 N·m

% 反作用轮角加速度
alpha_w = -tau_c / I_w;

% 反作用轮角速度（积分）
omega_w = ode45(@(t, omega) alpha_w, [0, 0.1], omega_w0);  % 时间步长0.1 s

---

二、卫星姿态控制算法的MATLAB实现

MATLAB支持经典控制（如PID）、现代控制（如LQR、滑模控制）、智能控制（如模糊控制、神经网络）等多种姿态控制算法。以下介绍PID控制（经典）、滑模控制（现代）的实现。

1. PID控制：姿态稳定的基础

PID控制是卫星姿态控制的经典方法，通过比例（P）、积分（I）、微分（D）三项协同作用，抑制误差。其控制律为：

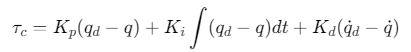
其中：

• \(K_p\)：比例增益（抑制当前误差）；
• \(K_i\)：积分增益（消除稳态误差）；
• \(K_d\)：微分增益（预测未来误差）。

MATLAB实现：

通过pid函数创建PID控制器，例如：

% PID控制器参数（示例）
Kp = 10;  % 比例增益
Ki = 5;   % 积分增益
Kd = 2;   % 微分增益

% 创建PID控制器
pid_controller = pid(Kp, Ki, Kd);

% 期望姿态（四元数）
q_d = [1; 0; 0; 0];  % 指向地球（假设）

% 当前姿态（四元数，含噪声）
q = [0.99; 0.01; 0.01; 0.01] + 0.001*randn(4,1);

% 姿态误差（四元数差）
q_error = quaternion_multiply(conj(q_d), q);  % 误差四元数

% 误差向量（取前三个元素）
e = q_error(2:4);

% 误差角速度（假设）
omega_d = [0; 0; 0];  % 期望角速度
omega = [0.1; 0.1; 0.1] + 0.01*randn(3,1);  % 当前角速度（含噪声）
e_omega = omega_d - omega;

% PID控制力矩
tau_c = pid_controller.step(e) + pid_controller.step(e_omega);  % 比例+微分项（积分项用于稳态）

2. 滑模控制：抗干扰的“利器”

滑模控制（SMC）是变结构控制的一种，通过设计滑模面（如\(s=e+λe˙，λ>0\)），使系统状态在有限时间内到达滑模面，并沿其滑向平衡点，从而完全免疫匹配干扰（如太阳辐射压）。

滑模控制律：

\(τ_c=τ_{eq}+τ_{sw}\)

其中：

• \(τ_{eq}\)：等效控制（维持系统在滑模面）；
• \(τ_{sw}\)：切换控制（将系统“拉”回滑模面，如\(τ_{sw}=−Ksign(s)\)，\(K>0\)）。

MATLAB实现：

通过smc函数或自定义函数实现滑模控制，例如：

% 滑模控制参数
lambda = 5;  % 滑模面参数（>0）
K = 10;      % 切换增益（>0）

% 滑模面（姿态误差+角速度误差）
s = e + lambda * e_omega;

% 等效控制（根据动力学方程推导）
tau_eq = I * (omega_d - omega) + cross(omega, I*omega);  % 假设tau_d=0

% 切换控制（抑制干扰）
tau_sw = -K * sign(s);

% 滑模控制力矩
tau_c = tau_eq + tau_sw;

---

三、卫星姿态控制系统的MATLAB仿真

MATLAB通过Simulink（可视化建模）和ODE45（数值求解）实现卫星姿态控制系统的仿真。以下介绍Simulink建模（常用）和ODE45数值仿真（自定义）的流程。

1. Simulink建模：可视化仿真平台

Simulink是MATLAB的可视化仿真工具，通过拖拽模块（如“State-Space”、“PID Controller”、“Scope”）构建卫星姿态控制系统模型。

Simulink模型结构：

• 被控对象：卫星姿态动力学模型（通过“State-Space”或“MATLAB Function”模块实现）；
• 控制器：PID或滑模控制模块（通过“PID Controller”或“MATLAB Function”模块实现）；
• 传感器：陀螺仪、星敏感器模块（通过“AWGN”模块添加噪声）；
• 执行机构：反作用轮模块（通过“Gain”模块模拟力矩输出）；
• 可视化：“Scope”模块显示姿态角、角速度、控制力矩等曲线。

示例模型（来自）：

• 动力学模块：输入控制力矩，输出角速度和姿态四元数；
• 运动学模块：输入角速度，输出姿态四元数；
• 控制器模块：输入姿态误差，输出控制力矩；
• 传感器模块：输入姿态四元数和角速度，输出带噪声的测量值；
• 执行机构模块：输入控制指令，输出控制力矩。

仿真结果：通过“Scope”模块查看姿态角（如滚转角）随时间的变化曲线，评估控制器的响应速度（如上升时间）、超调量（如最大偏差）、稳态误差（如最终偏差）。

2. ODE45数值仿真：自定义模型求解

对于复杂非线性模型（如大角度姿态机动），可通过ode45函数数值求解姿态动力学方程。ode45是MATLAB的变步长龙格-库塔求解器，适用于求解常微分方程组（ODEs）。

MATLAB实现：

定义姿态动力学方程的函数，例如：

function dy = satellite_dynamics(t, y, I, tau_c, tau_d)
    % y: 状态向量 [q0, q1, q2, q3, omega_x, omega_y, omega_z]
    % I: 转动惯量矩阵
    % tau_c: 控制力矩
    % tau_d: 外部扰动力矩
    
    % 提取状态
    q = y(1:4);
    omega = y(5:7);
    
    % 运动学方程
    dq = quaternion_kinematics(q, omega);
    
    % 动力学方程
    domega = inv(I) * (tau_c + tau_d - cross(omega, I*omega));
    
    % 状态导数
    dy = [dq; domega];
end

仿真流程：

1. 设置初始条件：如初始姿态四元数q0=[1;0;0;0]，初始角速度omega0=[0;0;0]；

2. 定义时间范围：如tspan=[0,10]（10秒仿真）；

调用ode45求解：

% 卫星参数
I = diag([10, 10, 10]);  % 转动惯量 (kg·m²)
tau_c = [5; 0; 0];       % 控制力矩 (N·m)
tau_d = [0.1; 0.1; 0.1]; % 外部扰动力矩 (N·m)

% 初始条件
y0 = [1; 0; 0; 0; 0; 0; 0];  % [q0, q1, q2, q3, omega_x, omega_y, omega_z]

% 时间范围
tspan = [0, 10];

% 调用ode45求解
[t, y] = ode45(@(t, y) satellite_dynamics(t, y, I, tau_c, tau_d), tspan, y0);

结果可视化：

通过plot函数绘制姿态角（如滚转角ϕ）、角速度（如ωx）随时间的变化曲线，例如：

% 提取姿态四元数和角速度
q = y(:, 1:4);
omega = y(:, 5:7);

% 计算滚转角（欧拉角）
roll = atan2(2*(q(:,1)*q(:,2) + q(:,3)*q(:,4)), q(:,1)^2 + q(:,4)^2 - q(:,2)^2 - q(:,3)^2);

% 绘制滚转角曲线
figure;
plot(t, roll);
xlabel('时间 (s)');
ylabel('滚转角 (rad)');
title('卫星滚转角随时间变化');
grid on;

参考代码 自动控制理论中卫星姿态控制系统 www.youwenfan.com/contentcno/84361.html

四、MATLAB在卫星姿态控制中的优势

1. 丰富的工具箱：Control System Toolbox（控制算法设计）、Simulink（可视化仿真）、Symbolic Math Toolbox（符号计算）等，覆盖卫星姿态控制的全流程；
2. 高效的数值求解：ode45、ode15s等求解器可快速求解复杂非线性微分方程，适用于大角度姿态机动仿真；
3. 可视化功能：通过“Scope”、“Plot”等工具直观展示姿态角、角速度、控制力矩等曲线，便于分析控制器性能；
4. 扩展性强：支持与MATLAB Function模块结合，实现自定义控制算法（如滑模控制、自适应控制），满足复杂任务需求。