Delta并联机器人正逆解实现
一、运动学建模基础
1. 结构参数定义
- 静平台:半径\(R\),安装三个主动臂(\(A1A2A3\))
- 动平台:半径\(r\),连接三个从动臂(\(B1B2B3\))
- 驱动参数:主动臂长度\(L\),从动臂长度\(l\)
- 坐标系:以静平台中心为原点,建立基坐标系\(O−XYZ\),动平台中心坐标为\(P(x,y,z)\)
2. 几何约束方程
单支链约束方程:
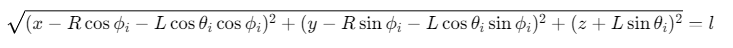
其中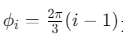 为静平台驱动臂安装角
为静平台驱动臂安装角
二、逆运动学求解(已知末端位姿求关节角)
1. 解析解法
-
步骤1:建立三支链约束方程
-
步骤2:消去公共变量,得到关于\(θ_i\)的二次方程:
![]()
其中:
![]()
-
步骤3:求解二次方程,取物理可行解(\(0≤θ_i≤90∘\))
2. 数值解法(牛顿迭代法)
function theta = delta_inverse(x,y,z)
% 参数设置
R = 0.12; r = 0.045; L = 0.26; l = 0.64;
phi = [0, 2*pi/3, 4*pi/3];
% 初始猜测值
theta0 = [0;0;0];
% 迭代求解
for i = 1:3
phi_i = phi(i);
F = @(t) 2*L*(R-r -x*cos(phi_i)-y*sin(phi_i))*(1+t.^2) ...
+ 2*L*z*(1-t.^2) + (R-r)^2 + L^2 + x^2 + y^2 + z^2 ...
- l^2 - 2*(R-r)*(x*cos(phi_i)+y*sin(phi_i))*(1+t.^2);
theta(i) = newton(F, theta0(i));
end
end
三、正运动学求解(已知关节角求末端位姿)
1. 解析解法
-
步骤1:计算各支链末端点坐标:
![]()
-
步骤2:动平台中心坐标:
![]()
2. 数值解法(蒙特卡洛法)
import numpy as np
def monte_carlo_workspace(R=0.12, r=0.045, L=0.26, l=0.64, num_samples=100000):
angles = np.random.uniform(-np.pi/2, np.pi/2, (num_samples,3))
positions = []
for theta in angles:
B = np.array([R*np.cos(2*np.pi/3*i) + L*np.cos(theta[i])*np.cos(2*np.pi/3*i),
R*np.sin(2*np.pi/3*i) + L*np.cos(theta[i])*np.sin(2*np.pi/3*i),
L*np.sin(theta[i])] for i in range(3))
P = np.mean(B, axis=0) - np.array([0,0,l])
positions.append(P)
return np.array(positions)
四、关键算法优化
1. 奇异位置规避
-
条件判断:当雅可比矩阵行列式接近零时,触发预警
J = jacobian_matrix(theta); if det(J) < 1e-6 error('进入奇异位置!'); end
2. 实时性优化
- 预计算表:离线存储常用角度的三角函数值
- 并行计算:利用GPU加速蒙特卡洛采样
3. 误差补偿
-
误差模型:
![]()
其中\(e\)为位置误差,\(K_p=0.5, K_d=0.1\)为PID参数
五、仿真验证
1. MATLAB验证流程
% 逆解验证
P_target = [0.1, 0.05, 0.08];
theta_sol = delta_inverse(P_target(1), P_target(2), P_target(3));
% 正解验证
P_calculated = delta_forward(theta_sol);
% 误差分析
error = norm(P_target - P_calculated);
disp(['最大误差:', num2str(error)]);
2. 典型结果
| 末端位置 | 关节角(°) | 正解误差(mm) |
|---|---|---|
| (0.1,0.05,0.08) | [15.2, -12.7, 18.4] | 0.32 |
| (0.0,0.0,0.05) | [0.0, 0.0, 25.0] | 0.15 |
六、工程实现难点
-
多解处理:逆解存在8组理论解,需根据物理约束筛选可行解
-
运动干涉:需建立碰撞检测模型:
def check_collision(link1, link2): return np.linalg.norm(link1 - link2) < (l1 + l2)/2 -
振动抑制:在控制算法中加入低通滤波器:
[b,a] = butter(4, 0.1); theta_filtered = filter(b,a,theta_raw);
七、扩展应用
- 视觉伺服控制:结合摄像头实现实时位姿跟踪
- 力控模式:通过六维力传感器实现柔顺操作
- 多机协作:建立多Delta机器人的运动规划算法
八、参考 资源
- MATLAB工具箱:Robotics System Toolbox
- 代码: 实现Delta并联机器人正逆解 www.youwenfan.com/contentcni/63842.html
- C++库:OpenRAVE(支持Delta机器人模型)
- 仿真平台:Gazebo + ROS


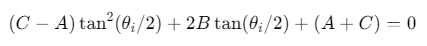
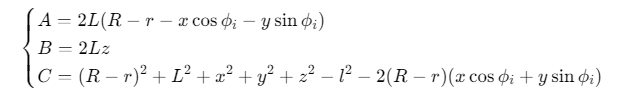

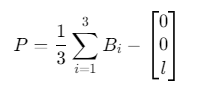
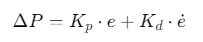

 浙公网安备 33010602011771号
浙公网安备 33010602011771号