存算一体单元的Bit Serial和Bit Parallel方式对比

存算目前的演进趋势是从bit serial变成了bit parallel，即乘法操作从1b*nb变成了nb*nb，并消除掉了原先bit serial设计中的累加器，值得一提的是tsmc那边的结论是等吞吐率情况下，加法树功耗接近，但移位累加的开销显著的少，因此bit parallel在ppa上全面优于bit serial，目前3nm上发布的最新工作也都在采用bit parallel的方法。

一个简单的量化比较思路，就以这里的256-inputs bit-serial和4*64-inputs bit parallel为例，首先两者的吞吐率相等，256-inputs bit-serial需要4个cycle完成全部的MAC，因此实际的tops要除以4，也就是64 INT4xINT4 MACs/cycle，而4*64-inputs bit parallel一个cycle完成，所以也是64 INT4xINT4 MACs/cycle。然后比较开销情况，公平起见，bit parallel的结果最后也要在4个cycle上去累加：

bit serial：256*1*4b 与门 （乘法器）， 128*4b 加法器 + 64*5b 加法器 + 32*6b 加法器 + 16*7b 加法器 + 8*8b 加法器 + 4*9b 加法器 + 2*10b 加法器 + 1*11b 加法器（加法树）， 16b 加法器 + 16b DFF + 16位移位mux（累加器）

bit parallel：64*4*4b 与门 + 64*2*4b加法器 + 64*5b加法器 （乘法器）， 32*8b 加法器 + 16*9b 加法器 + 8*10b 加法器 + 4*11b 加法器 + 2*12b 加法器 + 13b 加法器（加法树）， 16b 加法器 + 16b DFF（累加器）

这里的乘法器结构：

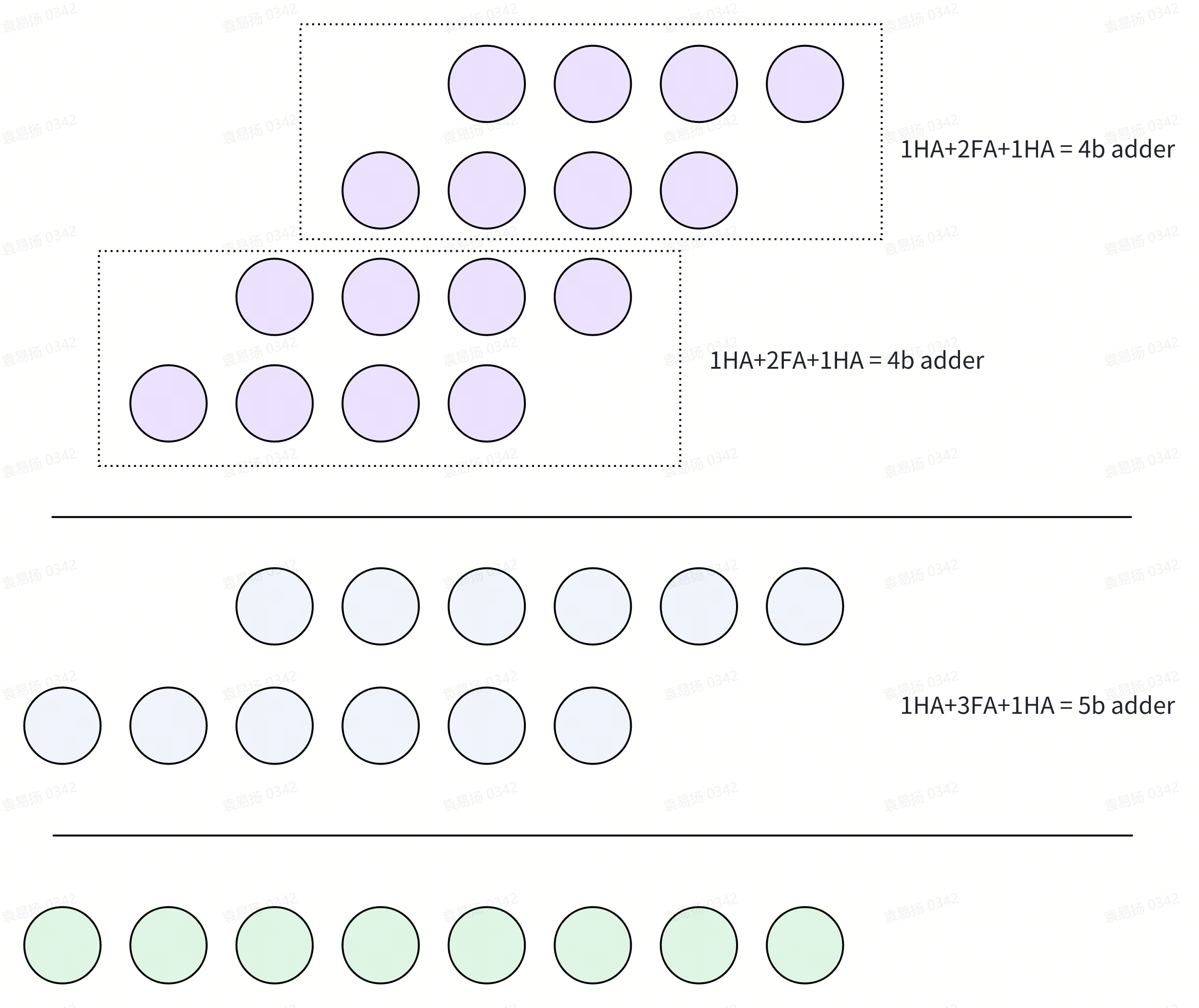
列表统计bit serial和bit parallel的情况，加法树中的每一级n bit加法器都是1b HA + n-1 FA：

	bit serial	bit parallel
AND	256*4=1024	64*4*4=1024
HA	128+64+32+16+8+4+2+1+1=256	64*2*2+64*2+32+16+8+4+2+1+1=448
FA	128*3+64*4+32*5+16*6+8*7+4*8+2*9+10+15=1027	64*2*2+64*3+32*7+16*8+8*9+4*10+2*11+12+15=961
DFF	16	16
MUX	16	0

• 表1

如果算的是n=8，N=32，K=32的bit serial的情况，bit serial（不考虑booth优化的事情）等吞吐率的bit parallel为n=8，N=32，K=4：

bit serial：32*1*8b与门 （乘法器）， 16*8b加法器+8*9b加法器+4*10b加法器+2*11b加法器+12b加法器（加法树），21b加法器+21b DFF+21b mux（累加器）

bit parallel：4*8*8b与门+4*4*8b加法器（2HA+6FA）+4*2*9b加法器（2HA+7FA）+4*1*10b（2HA+8FA）加法器（乘法器），2*16b加法器+1*17b加法器（加法树），21b加法器+21b DFF（累加器）

	bit serial	bit parallel
AND	32*8=256	4*8*8=256
HA	16+8+4+2+1+1=32	4*4*2+4*2*2+4*2+2+1+1=60
FA	16*7+8*8+4*9+2*10+11+20=263	4*4*6+4*2*7+4*8+2*15+16+20=250
DFF	21	21
MUX	21	0

• 表2

按2.5HA=1FA折算，bit serial是275.8FA，bit parallel是274FA。

如果考虑直接实现n=8，N=32，K=32的bit parallel结构，假定实现一个等吞吐率的bit parallel结构，则需要达到32*8=256bit的并行度，即n=8，N=32，K=256的bit serial结构：

bit serial：256*1*8b与门 （乘法器）， 128*8b加法器+64*9b加法器+32*10b加法器+16*11b加法器+8*12b加法器+4*13b+2*14b+15b（加法树），24b加法器+24b DFF+24b mux（累加器）

bit parallel：32*8*8b与门+32*4*8b加法器（2HA+6FA）+32*2*9b加法器（2HA+7FA）+32*1*10b（2HA+8FA）加法器（乘法器），16*16b加法器+8*17b加法器+4*18b加法器+2*19b加法器+20b加法器（加法树），24b加法器+24b DFF（累加器）

	bit serial	bit parallel
AND	256*8=2048	32*8*8=2048
HA	128+64+32+16+8+4+1+1=256	32*4*2+32*2*2+32*2+16+8+4+2+1+1=480
FA	128*7+64*8+32*9+16*10+8*11+4*12+14+23=2029	32*4*6+32*2*7+32*8+16*15+8*16+4*17+2*18+19+23=1986
DFF	24	24
MUX	24	0

• 表3

按2.5HA=1FA折算，bit serial是2131.4FA，bit parallel是2178FA。

而如果是均为n=8，N=32，K=32的情况下：

	bit serial	bit parallel
AND	32*8=256	32*8*8=2048
HA	16+8+4+2+1+1=32	32*4*2+32*2*2+32*2+16+8+4+2+1+1=480
FA	16*7+8*8+4*9+2*10+11+20=263	32*4*6+32*2*7+32*8+16*15+8*16+4*17+2*18+19+23=1986
DFF	21	0
MUX	21	0

• 表4

按2.5HA=1FA折算，bit serial是275.8FA，bit parallel是2178FA，两者对比开销基本上为1：8。

表1的分析结果和tsmc论文基本上一致，移位上bit parallel没有移位电路，因此会显著的减少掉累加开销；加法树上用这里的数据比较（乘法器里的两级加法也算进加法树），按2.5HA=1FA算，bit serial是1129.4FA，bit parallel是1140.2FA，bit parallel略大一些，但tsmc的电路做了特殊优化，乘法上没有用两个4b+一个5b的加法的做法，用了静态加法+LUT的做法，因此又扣出了一些加法树上的提升。进一步考虑3nm论文中讨论的bit parallel在实际场景下翻转率更低的优势，bit parallel在ppa上都有优势是完全合理的。

表2和表3分析的主要是展现bit serial和bit parallel在等吞吐率下，不同计算规模下的资源开销情况，再次折算比对的情况下，小并行度K=32的情况下会出现了bit parallel在加法开销上少于bit serial的情况，甚至都没有考虑静态加法+LUT优化的事情，何况还有累加上开销更小的进一步优势存在；在大并行度，即K=256的情况下，bit serial展现了相对bit parallel在加法树上的优势，且从趋势上来看，如果并行度进一步加大，那么bit serial的优势应该会更明显。

但是从架构上来考虑，bit parallel仍然更加友好，两方面考虑，一方面是计算的cycle数更少所以吞吐率很容易上去，而bit serial想达到相同的需要更高的并行度，但实际上并行度的选取必须要考虑实际应用中矩阵的形状，过大的并行度会导致计算单元的利用率低下，这也是为什么常规情况下tensor core设计时就不会取那么大的粒度，一般就是32，如果有更大规模的矩阵需要计算则采用分tiles的模式来完成。此外bit serial需要一个额外的并转串的输入处理电路，对于大规模并行结构来说，这部分的开销实际上也需要考虑，对于K个n bit的bit serial输入来说，需要Kn个DFF和K个n bit MUX，实际上这会是很大的一块开销，后续将进行量化评估。

此外从tops/mm2指标计算的角度来说，bit parallel会有更显著的优势，根据表4可以看出mac计算部分，等参数下bit parallel相比bit serial的开销大致等于n，而bit parallel的吞吐率比bit serial要大n倍，但两者的sram开销是一致的，这会导致在计算时sram的开销被多次重复，具体的理论分析如下：

定义cim的总面积\(A_{cim}\)为sram部分面积\(A_{sram}\)和mac部分面积\(A_{mac}\)之和，cim的吞吐率为\(T_{cim}\)，那么tops/mm2指标可以通过吞吐率除以cim面积进行计算。

\[A_{cim} = A_{sram} + A_{mac} \tag{1} \]

\[AF=T_{cim}/A_{cim} \tag{2} \]

针对表4的bit serial和bit parallel相同通道数的情况，分别定义bit parallel的总面积\(A_{pcim}\)，mac部分面积\(A_{pmac}\)，吞吐率\(T_{pcim}\)；bit serial的总面积\(A_{scim}\)，mac部分面积\(A_{smac}\)，吞吐率\(T_{scim}\)，在计算位数为n的情况下有：

\[A_{pmac} = n \times A_{smac} \tag{3} \]

\[T_{pmac}=n \times T_{smac} \tag{4} \]

将（3）和（4）分别代入到bit parallel和bit serial的tops/mm2指标的计算中，定义bit parallel的tops/mm2为\(AF_{pcim}\)，bit serial的tops/mm2为\(AF_{scim}\)，有：

\[AF_{pmac}=\frac{T_{pmac}}{A_{sram}+A_{pmac}} = \frac{n \times T_{smac}}{A_{sram}+n\times A_{smac}} = \frac{T_{smac}}{A_{sram}/n + A_{smac}} \gt \frac{T_{smac}}{A_{sram}+A_{smac}} = AF_{smac} \tag{5} \]

很明显可以看到，由于sram的面积开销在n bit的bit parallel中可以得到有效的均摊，因此会出现tops/mm2占优的情况，尤其是在sram面积占比更大的大存算比情况时，bit parallel的tops/mm2优势会更加的显著。