KMP 算法

在字符串匹配问题中，通常面临这样的任务：给定一个文本串 \(S_1\) 和一个模式串 \(S_2\)，找出 \(S_2\) 在 \(S_1\) 中出现的位置。

最直观的方法是暴力匹配：从 \(S_1\) 的第一个字符开始，逐个比较 \(S_2\)；如果匹配失败，\(S_1\) 的指针向后移动一位，\(S_2\) 的指针回到开头重新匹配。这种方法的时间复杂度最坏是 \(O(|S_1| \times |S_2|)\)，如果字符串比较随机，暴力匹配的效率是不低的，但可以构造测试数据，使暴力匹配的做法超时。暴力匹配效率低是因为比对失败时还需要从头开始匹配，在失配（匹配失败）之后，如果可以利用已经匹配过的信息，将 \(S_2\) 尽可能多地向右“滑动”一段距离，就可以提升效率，这就是 KMP（Knuth-Morris-Pratt）算法的优化思路。

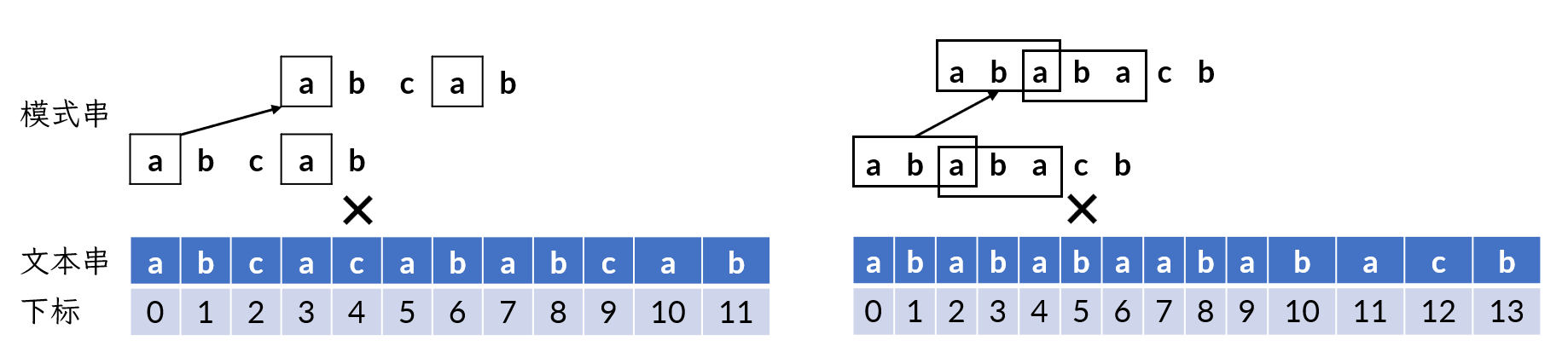
例如，文本串是“abcacababcab”，模式串是“abcab”，首先将文本串和模式串放在一起进行匹配，发现文本串第 4 个字符“c”（这里定义字符串开头是第 0 个字符）和模式串第 4 个字符“b”失配。这时将模式串向右移动 3 位，使移动后的第 0 位和移动前的第 3 位对齐，然后继续判断匹配。同理，对于另外一个例子：当模式串第 5 位失配时，可以发现第 0 位到第 2 位的子串和第 2 位到第 4 位的子串是是一样的，将模式串往后移动两位，然后继续尝试匹配。

像这样，对于模式串的每一位，都存在唯一的“特定变化位数”：在这一位失配时，可以直接将模式串往右移动这一“特定变化位数”。可以发现，对于左边的例子来说，模式串第 4 位失配时，考察第 0 位到第 3 位这个子串，它的前缀“a”和后缀“a”是相同的；对于右边的例子来说，模式串第 5 位失配时，考察第 0 位到第 5 位这个子串，它的前缀“aba”和后缀“aba”是相同的。像这样前缀和后缀相同的情况下，在失配前，模式串的后缀已经验证了可以和文本串匹配，那么这个前缀也是可以匹配的，不需要重复枚举匹配。这对相同的前缀和后缀，通常称为 border。

如何获得模式串的每个前缀 \(S'\) 的最长 border \(T'\) 的长度呢？朴素枚举的做法是针对每个模式串的每一个前缀，依次枚举它的前缀和后缀长度，然后比较这两个子串是否相同。这种做法的时间复杂度很高，因此需要进一步优化。

令模式串第 0 位到第 \(i\) 位的子串的最长 border 的长度为 \(b_i\)，将其称为前缀函数。可以发现，在已经得到 \(b_{i-1}\) 的情况下，可以递推出 \(b_i\) 的结果。如上图，已知 \(b_{i-1}=3\)，计算 \(b_i\) 的时候，如果发现 \(S_3\) 等于 \(S_i\)，则可以借助之前已经记录的信息，得到 \(b_i = b_{i-1}+1\) 的结论。可以利用反证法证明：\(b_i\) 最多比 \(b_{i-1}\) 多 \(1\)，不可能多更多。如果 \(S_3 \ne S_i\)，则继续尝试枚举更短的前后缀并判断是否相同，然后继续尝试匹配。考察枚举更短前后缀的循环，如果需要缩减一次前后缀长度，则必须有对应的增加前后缀的长度的过程，而增加的次数不会超过 \(|S|\)，所以减少长度的次数也不会超过 \(|S|\)。因此，这种做法的时间复杂度是 \(O(|S|^2)\)。

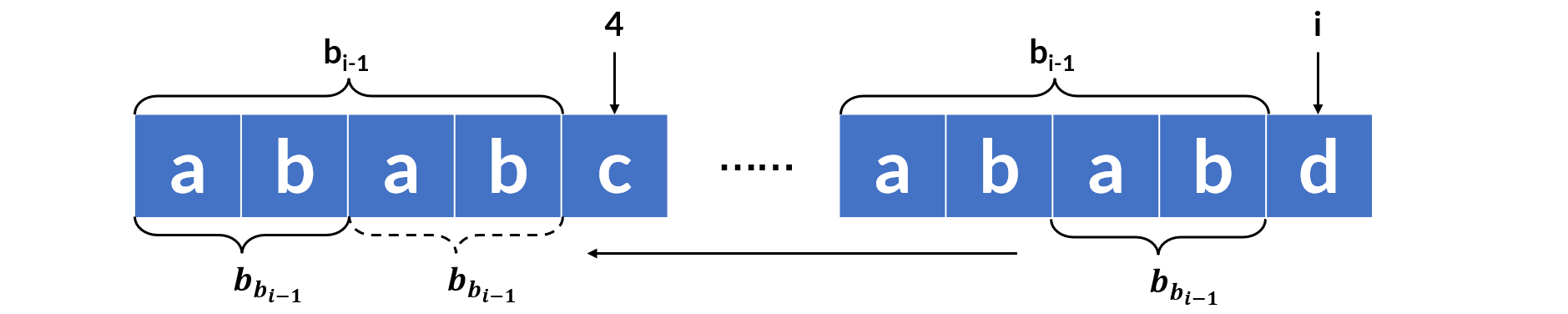
实际上，找到更短 border 的过程也可以优化。如上图所示，\(b_{i-1}=4\)，发现 \(S_4 \ne S_i\)，因此需要找 \(S_{0 \dots i-1}\) 子串中次短的 border。由于 \(S_{0 \dots 3} = S_{i-4 \dots i-1}\)，所以计算 \(S_{0 \dots i-1}\) 子串中次短的 border 长度就是 \(S_{0 \dots b_{i-1}-1}\) 的最长 border 长度，即 \(b_{b_{i-1}}\)。如果发现还是不能匹配，则可以继续迭代，继续缩短长度。这种做法不需要判断子串是否相同，时间复杂度是 \(O(|S|)\)。

于是，如何借助前缀函数进行字符串匹配的做法就显而易见了：首先将模式串和文本串的开头对齐，然后比较文本串和模式串的第 0 位是否一致，如果一致则继续匹配下一位；如果不匹配则将模式串往右移动，使它的左 border 和它原来的右 border 重合，这种算法就是 KMP 算法。代码实现中，可以将模式串的指针设为 \(j\)，将文本串的指针设为 \(i\)，如果失配，则将 \(j\) 的值设置为 \(b_{j-1}\)；当匹配完所有的模式串字符，说明找到了一个匹配，根据 \(i\) 的位置推导出匹配到的位置。

例题：P3375 【模板】KMP

参考代码

#include <cstdio>
#include <cstring>

const int N = 1e6 + 5;
char s1[N], s2[N];
// b[i] 表示 s2 中以 i 结尾的前缀子串的最长相等前后缀长度 (border 长度)
int b[N];

int main()
{
    // 读取两个字符串，s1 是文本串，s2 是模式串
    scanf("%s%s", s1, s2);
    int n = strlen(s1), m = strlen(s2);

    // --- 计算 b 数组 (前缀函数的计算) ---
    // b[0] 必然为 0，因为 border 不能是本身
    b[0] = 0;
    // i 从 1 开始遍历 s2，j 表示当前匹配的最长前缀长度 (也是前一个位置的 border 长度)
    for (int i = 1, j = 0; i < m; i++) {
        // 如果当前字符 s2[i] 不匹配 s2[j] (j 同时也是下一个待匹配字符的下标)，
        // 则回退 j 到上一个 border 的长度，直到匹配或 j 归零
        while (j > 0 && s2[i] != s2[j]) j = b[j - 1];
        // 如果匹配，最长前缀长度 +1
        if (s2[i] == s2[j]) j++;
        // 记录 s2[0...i] 的最长 border 长度
        b[i] = j;
    }

    // --- KMP 匹配过程 ---
    // i 遍历文本串 s1，j 表示当前 s2 已匹配的长度
    for (int i = 0, j = 0; i < n; i++) {
        // 如果 s1 当前字符与 s2 下一个字符不匹配，回退 j
        while (j > 0 && s1[i] != s2[j]) j = b[j - 1];
        // 如果匹配，s2 的匹配长度 +1
        if (s1[i] == s2[j]) j++;
        // 如果 j 等于 m，说明 s2 已经完全匹配
        if (j == m) {
            // 输出匹配位置 (题目要求 1-based index)
            // i 是结束位置 (0-based)，起始位置是 i - m + 1
            // 转换为 1-based 需要 +1，即 i - m + 2
            printf("%d\n", i - m + 2);
            // 继续寻找下一次匹配，利用 border 性质回退
            // 这里不能重置 j=0，因为可能存在重叠匹配
            j = b[j - 1];
        }
    }

    // --- 输出 next 数组 ---
    // 题目要求输出 s2 每个前缀的最长 border 长度
    for (int i = 0; i < m; i++) printf("%d ", b[i]);
    
    return 0;
}

例题：P4391 [BalticOI 2009] Radio Transmission 无线传输

假设字符串 \(S\) 的长度为 \(L\)，其最长相等前后缀长度为 \(B_{L-1}\)，要求的循环节长度为 \(K\)。

由于前缀 \(S_{0 \dots B_{L-1}-1}\) 与后缀 \(S_{L-B_{L-1} \dots L-1}\) 相等，这意味着如果把字符串 \(S\) 向右平移 \(L-B_{L-1}\) 位，原本的后缀部分会和原本的前缀部分重合，这隐含了性质 \(S_i = S_{i + (L-B_{L-1})}\)。因此，\(L - B_{L-1}\) 是一个合法的循环节长度。

要使循环节长度 \(K\) 最小，就需要 \(L-K\) 最大，而 \(L-K\) 正是相等前后缀的长度。因为 \(B_{L-1}\) 代表的是最长相等前缀后缀的长度，所以 \(L-B_{L-1}\) 计算出的就是最短的循环节长度。

参考代码

#include <cstdio>

const int N = 1e6 + 5;
char s[N];
int b[N]; // b[i] 表示字符串 s[0...i] 的最长相等前后缀的长度（即 KMP 中的 border 数组）

int main()
{
    int l; 
    // 读取字符串长度和字符串内容
    scanf("%d%s", &l, s);
    
    // KMP 预处理：计算前缀函数 b 数组
    b[0] = 0;
    for (int i = 1; i < l; i++) {
        int j = b[i - 1];
        // 匹配失败时，回溯到上一个可能匹配的位置
        while (j > 0 && s[i] != s[j]) j = b[j - 1];
        // 如果当前字符匹配成功，长度加 1
        if (s[i] == s[j]) j++;
        b[i] = j;
    }
    
    // 结论：对于长度为 l 的字符串，其最短循环节的长度为 l - b[l-1]
    // 其中 b[l-1] 是整个字符串的最长相等前后缀长度
    printf("%d\n", l - b[l - 1]);
    
    return 0;
}