无向图的割边与边双连通分量
割边:对于一个无向图,如果删掉其中某条边后图中的连通块个数增加了,则称这条边为割边或桥。
割边的判定:对于 DFS 树中的节点 \(u\) 与其子节点 \(v\),满足 \(low_v > dfn_u\),则说明边 \(u \leftrightarrow v\) 是割边,因为这种情况下从 \(v\) 出发,在不经过 \(u \leftrightarrow v\) 这条边的情况下不管怎么走都无法到达 \(u\) 或 DFS 树上更早的节点。
和割点的判定对比可以发现,就差一个等号,这是由于在割点判定时允许走 \(u \leftrightarrow v\) 的反边更新 \(low\) 值,而割边判定时不允许走反边来更新 \(low\) 值。
struct Edge {
int x, y;
};
Edge e[M]; // 边集
vector<int> g[N]; // 这里存的是边的编号
int n, m, dfn[N], low[N], tot;
bool b[M]; // 是否为割边
void build() {
for (int i = 1; i <= m; i++) {
int x = e[i].x, y = e[i].y;
g[x].push_back(i);
g[y].push_back(i);
}
}
void tarjan(int u, int from) {
dfn[u] = low[u] = ++tot;
for (int i : g[u]) {
if (i == from) continue; // 避免回边
int v = e[i].x == u ? e[i].y : e[i].x;
if (!dfn[v]) {
tarjan(v, i);
low[u] = min(low[u], low[v]);
if (low[v] > dfn[u]) {
b[i] = true; // 这条边是割边
}
} else {
low[u] = min(low[u], dfn[v]);
}
}
}
边双连通分量:无向图中极大的不包含割边的连通块被称为边双连通分量(edge Double Connected Components,eDCC)。

通过之前的算法找到所有的割边后,只需要在原图上将割边屏蔽进行遍历,每次找到的连通块就是一个边双连通分量。
例题:P8436 【模板】边双连通分量
参考代码
#include <cstdio>
#include <vector>
#include <algorithm>
using std::vector;
using std::min;
const int N = 500005;
const int M = 2000005;
struct Edge {
int x, y;
};
Edge e[M];
bool b[M], vis[N];
vector<int> g[N], eDCC[N];
int dfn[N], low[N], tot, cnt;
void tarjan(int u, int from) {
dfn[u] = low[u] = ++tot;
for (int i : g[u]) {
if (i == from) continue;
int v = e[i].x == u ? e[i].y : e[i].x;
if (!dfn[v]) {
tarjan(v, i);
low[u] = min(low[u], low[v]);
if (low[v] > dfn[u]) {
b[i] = true;
}
} else {
low[u] = min(low[u], dfn[v]);
}
}
}
void dfs(int u) {
vis[u] = true; eDCC[cnt].push_back(u);
for (int i : g[u]) {
if (b[i]) continue;
int v = e[i].x == u ? e[i].y : e[i].x;
if (!vis[v]) dfs(v);
}
}
int main()
{
int n, m; scanf("%d%d", &n, &m);
for (int i = 1; i <= m; i++) {
int x, y; scanf("%d%d", &x, &y);
e[i] = {x, y};
g[x].push_back(i); g[y].push_back(i);
}
for (int i = 1; i <= n; i++) if (!dfn[i]) tarjan(i, 0);
for (int i = 1; i <= n; i++)
if (!vis[i]) {
cnt++;
dfs(i);
}
printf("%d\n", cnt);
for (int i = 1; i <= cnt; i++) {
printf("%d", (int)eDCC[i].size());
for (int j : eDCC[i]) {
printf(" %d", j);
}
printf("\n");
}
return 0;
}
习题:P2860 [USACO06JAN] Redundant Paths G
解题思路
希望每对点都有“两条独立的路线”(至少两条没有交集的路径),要达到这个效果等价于整个图是一个边双连通分量。因为整个图是边双连通分量意味着没有割边,而割边是某两个点的所有路径中的必经之路。因此本题相当于加若干条边,使得图中没有割边,变成一个独立的边双连通分量。
对原图中的所有边双连通分量缩点,得到的新图(实际上会是一棵树)中的边都是原图中的割边,显然如果在两个叶子节点之间连一条边,则这两个叶子节点之间的原始路径上的边都不再是割边。因此本题相当于使加的边对应的链的能够覆盖原来所有的割边。
一个容易猜到的结论是将叶子节点两两配对,假如共 \(c\) 个叶子节点,则最少需要添加 \(\left \lceil \dfrac{c}{2} \right \rceil\) 条边。
那么具体方案是怎么得到的呢?注意并不是随便两两配对加边就能变成一个 eDCC。
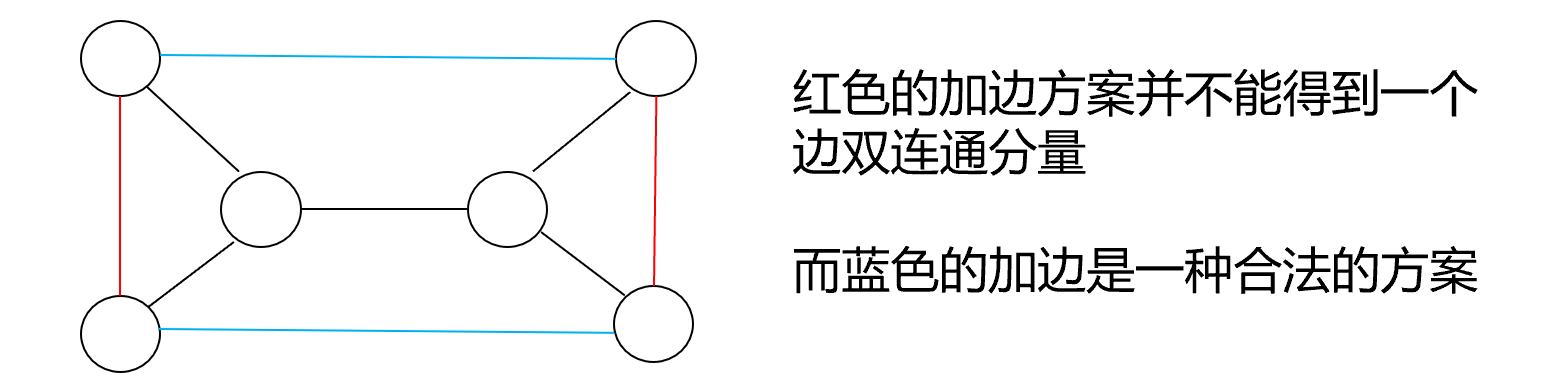
考虑对缩点后的树选一个根节点,使得其每个子节点下的子树中叶节点最多不超过 \(\left \lceil \dfrac{c}{2} \right \rceil\),可以证明肯定能找到这样的根节点。因为如果某棵子树中叶节点数量超了,可以通过调整法将根节点向该子树方向调整(类似于树的重心的原理)。此时可以证明一定有方案使得每次用来配对的叶子节点属于根节点的不同子树,只需要每次从剩余叶子节点最多的子树中拿一个叶子节点出来与其他子树的叶子节点配对,而这样配对过程中涉及到的链的并集会覆盖所有原来的割边。
参考代码
#include <cstdio>
#include <vector>
#include <algorithm>
using std::vector;
using std::min;
using std::max;
const int N = 5005;
const int M = 10005;
struct Edge {
int x, y;
};
Edge e[M];
bool b[M], vis[N];
vector<int> g[N];
int dfn[N], low[N], tot, eDCC[N], cnt, d[N];
void tarjan(int u, int from) {
dfn[u] = low[u] = ++tot;
for (int i : g[u]) {
if (i == from) continue;
int v = e[i].x ^ e[i].y ^ u;
if (!dfn[v]) {
tarjan(v, i);
low[u] = min(low[u], low[v]);
if (low[v] > dfn[u]) {
b[i] = true;
}
} else {
low[u] = min(low[u], dfn[v]);
}
}
}
void dfs(int u) {
vis[u] = true; eDCC[u] = cnt;
for (int i : g[u]) {
if (b[i]) continue;
int v = e[i].x ^ e[i].y ^ u;
if (!vis[v]) dfs(v);
}
}
int main()
{
int f, r; scanf("%d%d", &f, &r);
for (int i = 1; i <= r; i++) {
int x, y; scanf("%d%d", &x, &y);
e[i] = {x, y};
g[x].push_back(i); g[y].push_back(i);
}
for (int i = 1; i <= f; i++)
if (!dfn[i]) tarjan(i, 0);
for (int i = 1; i <= f; i++)
if (!vis[i]) {
cnt++;
dfs(i);
}
for (int i = 1; i <= r; i++) {
int x = e[i].x, y = e[i].y;
if (eDCC[x] != eDCC[y]) {
d[eDCC[x]]++; d[eDCC[y]]++;
}
}
int ans = 0;
for (int i = 1; i <= cnt; i++) {
if (d[i] == 1) ans++;
}
printf("%d\n", (ans + 1) / 2);
return 0;
}
习题:P8867 [NOIP2022] 建造军营
解题思路
测试点 \(1 \sim 7\)
这部分数据点和边的数量都不多,考虑枚举每个点是否建造军营,有 \(O(2^n)\) 种情况。
在一种特定的军营建造方案下,如果某条边断开之后会有军营之间无法连通,则这条边必须守卫,否则这条边可守可不守,因此可以计算出必须守卫的边的数量 \(c\),那么此时有 \(2^{m-c}\) 种边的守卫情况。这个过程枚举每条要断开的边,从某个军营出发对图做 DFS,如果存在一个到达不了的军营则这条边必须要守卫。
时间复杂度为 \(O(m(n+m)2^n)\)。
测试点 \(10 \sim 11\)
链的情况。此时如果选了某些点建兵营,则需要守卫最靠近两端的兵营之间的每一条边,具体地:
- 如果只选一个点建兵营,则每一条边都可守可不守,方案数为 \(n \times 2^m\)
- 如果选不止一个点,设编号最小的为 \(x\),编号最大的为 \(y\),则中间的 \(y-x\) 条边必须守卫,剩下的边有 \(2^{m-(y-x)}\) 种守卫情况,而 \(x+1\) 到 \(y-1\) 的兵营可建可不建,情况为 \(2^{y-x-1}\),总方案数为 \(2^{m-1}\),与 \(x\) 和 \(y\) 无关。而取出 \(x\) 和 \(y\) 的取法有 \(\dfrac{n(n-1)}{2}\) 种,因此总的方案数为 \(\dfrac{n(n-1)}{2} \times 2^{m-1}\)
参考代码
#include <cstdio>
#include <vector>
using std::vector;
const int N = 500005;
const int M = 1000005;
const int MOD = 1000000007;
vector<int> g[N];
int e[M], val, ban, p2[M];
bool vis[N];
void dfs(int u) {
vis[u] = true;
val |= 1 << (u - 1);
for (int i : g[u]) {
if (i == ban) continue;
int v = u ^ e[i];
if (!vis[v]) dfs(v);
}
}
int main()
{
int n, m; scanf("%d%d", &n, &m);
p2[0] = 1;
bool chain = (m == n - 1);
for (int i = 1; i <= m; i++) {
int u, v; scanf("%d%d", &u, &v);
if (u + 1 != v && v + 1 != u) chain = false;
e[i] = u ^ v;
g[u].push_back(i); g[v].push_back(i);
p2[i] = 2ll * p2[i - 1] % MOD;
}
if (chain) {
int res = 1ll * n * p2[m] % MOD;
res = (res + 1ll * n * (n - 1) / 2 % MOD * p2[m - 1] % MOD) % MOD;
printf("%d\n", res);
return 0;
}
int ans = 0;
for (int i = 1; i < (1 << n); i++) { // 枚举选点方案
int s = 0;
for (int j = 0; j < n; j++)
if (i & (1 << j)) {
s = j + 1; break;
}
int cnt = 0;
for (int j = 1; j <= m; j++) { // 枚举每条边
val = 0; ban = j;
for (int k = 1; k <= n; k++) vis[k] = false;
dfs(s); // 在不使用j这条边的情况下从s出发能到达哪些点
if ((i & val) != i) cnt++; // 这条边必须守
}
ans = (ans + p2[m - cnt]) % MOD;
}
printf("%d\n", ans);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号